Enoncé de l'exercice n° 8-1 : (Extrait : n°4 page 167 livre 2nde Hachette Education)
Dans un repère orthonormé, on considère les points suivants :
| \(\displaystyle A\left(-5;8\right)\) | \(\displaystyle B\left(6;5\right)\) | \(\displaystyle C\left(-1;3\right)\) | \(\displaystyle D\left(3;2\right)\) | \(\displaystyle E\left(7;-7\right)\) |
Question 1 : Les points \(\displaystyle A\), \(\displaystyle C\) et \(\displaystyle E\) sont-ils alignés ?
Question 2 : Les droites \(\displaystyle \left(AB\right)\) et \(\displaystyle \left(CD\right)\) sont-elles parallèles ?
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 8-2 : (Extrait : n°5 page 167 livre 2nde Hachette Education)
Dans un repère orthonormé, on considère les points suivants :
| \(\displaystyle A\left(2;6\right)\) | \(\displaystyle B\left(-3;5\right)\) | \(\displaystyle C\left(4;1\right)\) | \(\displaystyle D\left(-8;-1\right)\) | \(\displaystyle E\left(6;-4\right)\) |
Question 1 : Les points \(\displaystyle A\), \(\displaystyle C\) et \(\displaystyle E\) sont-ils alignés ?
Question 2 : Les droites \(\displaystyle \left(AB\right)\) et \(\displaystyle \left(CD\right)\) sont-elles parallèles ?
Question 3 : Le triangle \(\displaystyle BCD\) est-il isocèle ?
Envoyer la proposition de travail
Lancer l'interactivité
On considère les points \(\displaystyle A\left(2;3\right)\) , \(\displaystyle B\left(1;-1\right)\) et \(\displaystyle C\left(6;2\right)\)
Question 1 : Démontrer que le triangle \(\displaystyle ABC\) est rectangle et isocèle.
Question 2 : Calculer les coordonnées du point \(\displaystyle D\) tel que \(\displaystyle ABCD\) soit un carré.
Envoyer la proposition de travail
Lancer l'interactivité
On considère les points \(\displaystyle A\left(-1;4\right)\) , \(\displaystyle B\left(5;2\right)\) et \(\displaystyle M\left(x;y\right)\).
Question 1 : Calculer les coordonnées du milieu \(\displaystyle I\) de \(\displaystyle \left[AB\right]\).
Question 2 : Exprimer les coordonnées de \(\displaystyle \overrightarrow{MA}\), \(\displaystyle \overrightarrow{MB}\) et \(\displaystyle \overrightarrow{MI}\) en fonction de \(\displaystyle x\) et de \(\displaystyle y\).
Question 3 : Démontrer que \(\displaystyle \overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\).
Envoyer la proposition de travail
Lancer l'interactivité
On considère les points \(\displaystyle A\left(-2;5\right)\) , \(\displaystyle B\left(2;-2\right)\) et \(\displaystyle C\left(6;3\right)\).
Question 1 : Déterminer les coordonnées du point \(\displaystyle D\), défini par \(\displaystyle \overrightarrow{AD}=\frac{3}{2}\overrightarrow{AC}\).
Question 2 : Déterminer les coordonnées du point \(\displaystyle E\), défini par \(\displaystyle \overrightarrow{BE}=\frac{-1}{8}\overrightarrow{BA}+\frac{3}{8}\overrightarrow{BC}\).
Question 3 : Démontrer que les points \(\displaystyle B\), \(\displaystyle D\) et \(\displaystyle E\) sont alignés.
Envoyer la proposition de travail
Lancer l'interactivité
On considère les points \(\displaystyle A\left(-2;-3\right)\) , \(\displaystyle B\left(3;3\right)\) et \(\displaystyle C\left(4;-1\right)\). L'origine du repère est le point \(\displaystyle O\) et on note \(\displaystyle I\) le milieu de \(\displaystyle \left[AC\right]\).
Question 1 : Calculer les coordonnées du point \(\displaystyle P\), défini par \(\displaystyle \overrightarrow{OP}=\overrightarrow{OA}-2\overrightarrow{OB}+\overrightarrow{OC}\).
Question 2 : Démontrer que les droites \(\displaystyle \left(OP\right)\) et \(\displaystyle \left(IB\right)\) sont parallèles.
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 8-7 : (Extrait : Exercice n°64 page 175 Déclic 2nde Hachette)
Dans un repère orthonormé \(\displaystyle \left(O;I;J\right)\) on considère les points \(\displaystyle A\left(-4;2\right)\), \(\displaystyle B\left(4;-6\right)\), \(\displaystyle C\left(8;6\right)\), \(\displaystyle D\left(3;1\right)\) et \(\displaystyle E\left(0;-2\right)\)
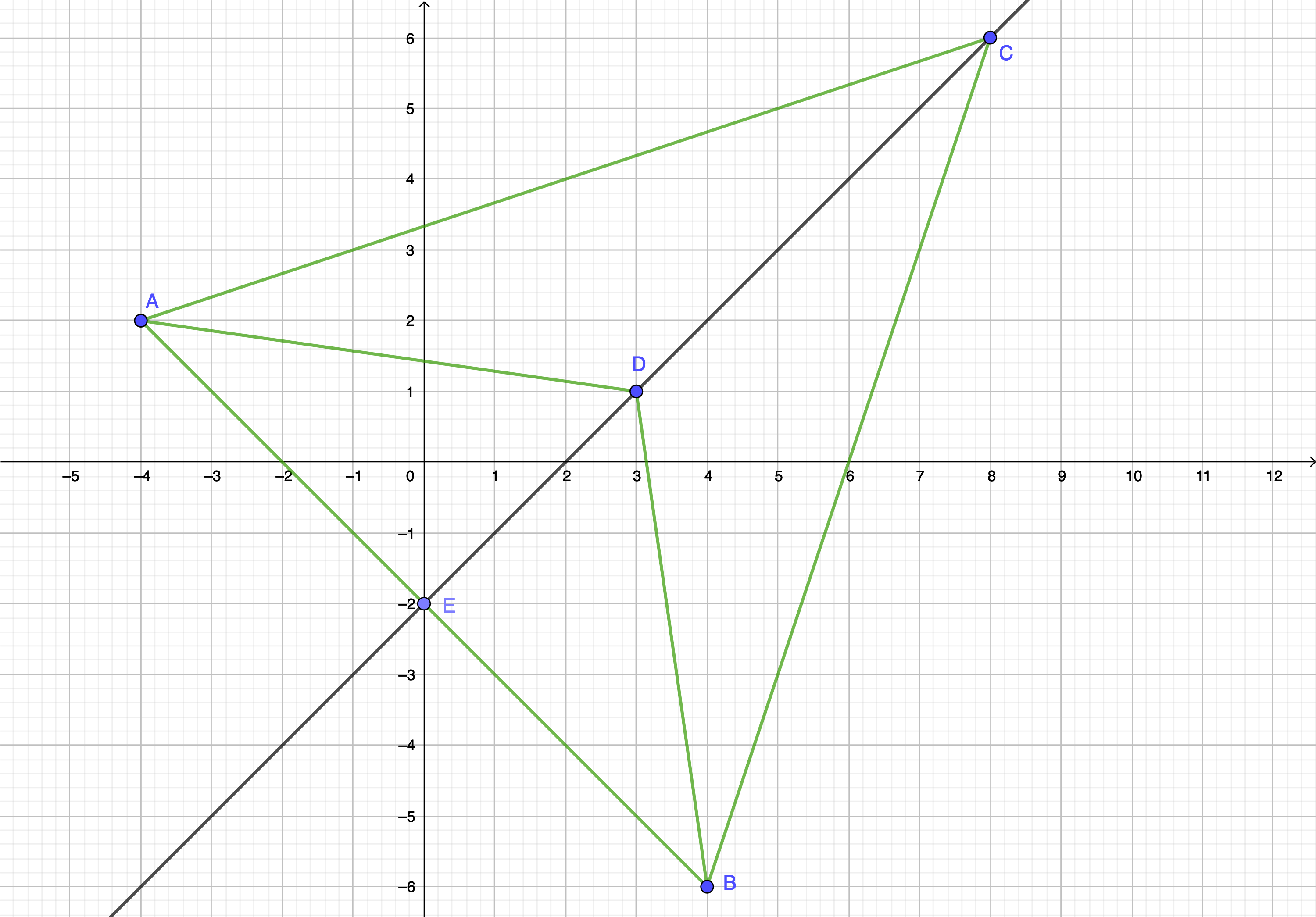
Question 1 : Montrer que le point \(\displaystyle D\) appartient à la médiatrice du segment \(\displaystyle \left[AB\right]\).
Question 2 : Déterminer la nature du triangle \(\displaystyle ABC\).
Question 3 : En déduire que \(\displaystyle \left(AB\right)\) et \(\displaystyle \left(CD\right)\) sont perpendiculaires.
Question 4 : Le point \(\displaystyle D\) est-il le milieu du segment \(\displaystyle \left[CE\right]\) ?
Question 5 : Calculer l'aire du triangle \(\displaystyle ABC\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 8-8 : (Extrait : Exercice n°84 page 178 Déclic 2nde Hachette)
Dans un repère orthonormé \(\displaystyle \left(O;I;J\right)\) on considère les points \(\displaystyle O\left(4;4\right)\), \(\displaystyle A\left(-1;4\right)\), \(\displaystyle B\left(8;7\right)\), \(\displaystyle C\left(0;1\right)\) , \(\displaystyle D\left(7;0\right)\) , \(\displaystyle T\left(1;8\right)\) et \(\displaystyle M\left(-7;2\right)\). La situation est résumée dans le schéma suivant :
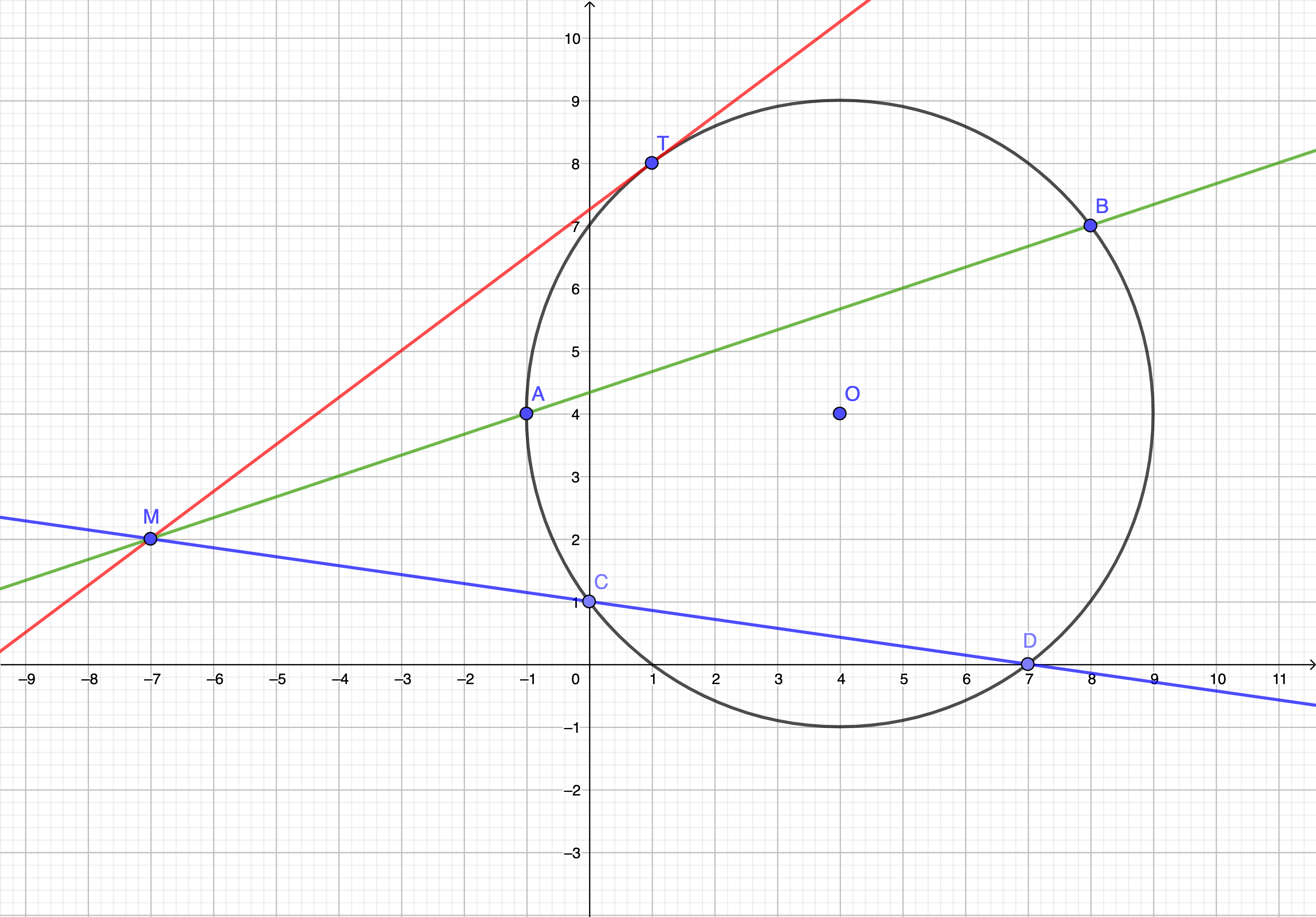
Question 1 : Justifier que les points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) et \(\displaystyle T\) appartiennent à un même cercle \(\displaystyle \mathcal{C}\) de centre \(\displaystyle O\).
Question 2 : Les points \(\displaystyle M\), \(\displaystyle A\) et \(\displaystyle B\) sont-ils alignés ?
Question 3 : Les points \(\displaystyle M\), \(\displaystyle C\) et \(\displaystyle D\) sont-ils alignés ?
Question 4 : Comparer les produits : \(\displaystyle MA\times MB\) ; \(\displaystyle MC\times MD\) et \(\displaystyle MT^2\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 8-9 : (Extrait : Exercice n°85 page 178 Déclic 2nde Hachette)
Dans un repère orthonormé \(\displaystyle \left(O;I;J\right)\) on considère les points \(\displaystyle A\left(2;4\right)\), \(\displaystyle B\left(-1;2\right)\) et \(\displaystyle C\left(6;-2\right)\).
On note \(\displaystyle \mathcal{C}\) le cercle circonscrit au triangle \(\displaystyle ABC\). La situation est résumée dans la figure suivante :
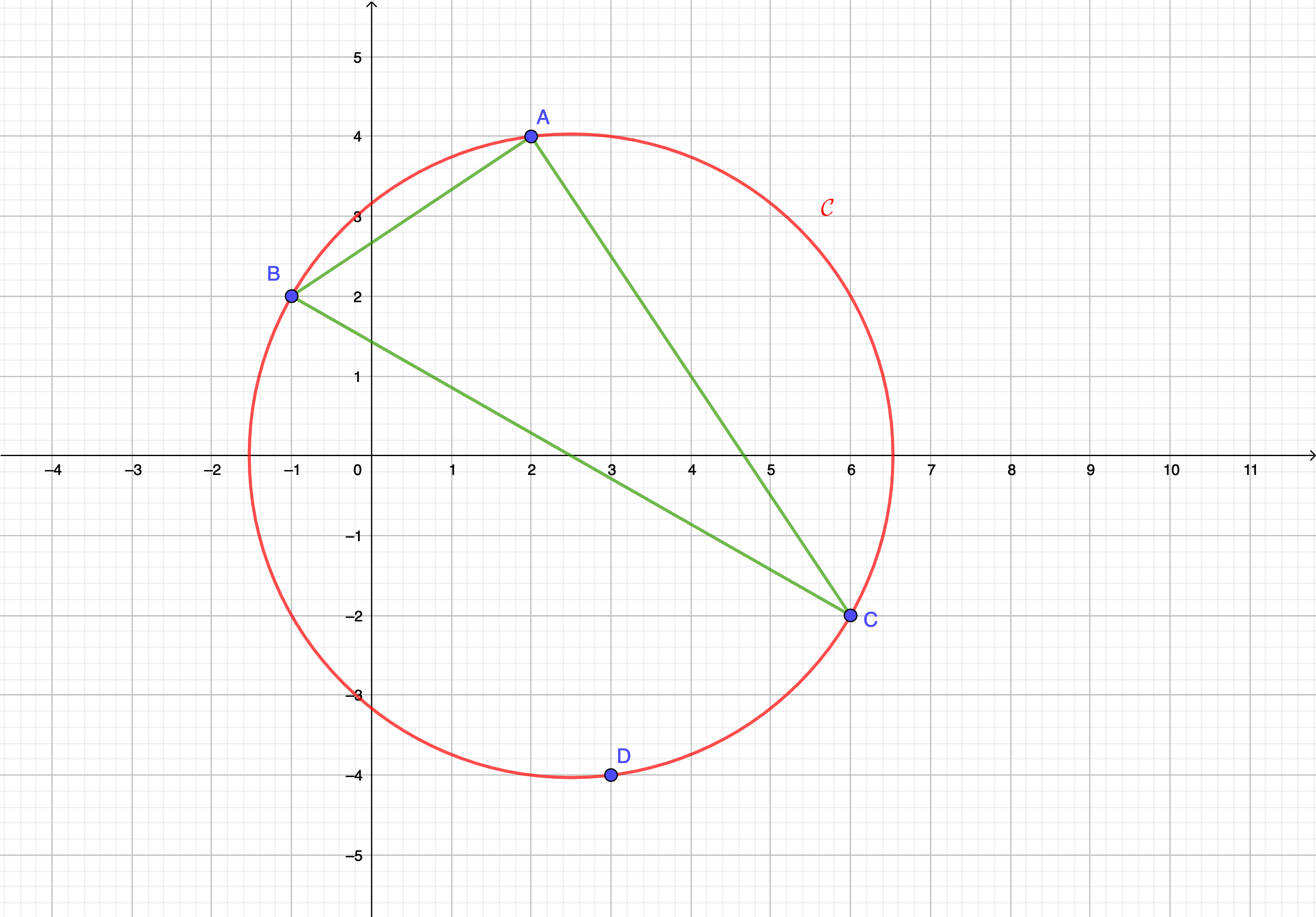
Question 1 : Donner la nature du triangle \(\displaystyle ABC\).
Question 2 : Déterminer le centre et le rayon du cercle \(\displaystyle \mathcal{C}\).
Question 3 : Justifier si le point \(\displaystyle D\left(3;-4\right)\) appartient au cercle \(\displaystyle \mathcal{C}\).
Question 4 : Déterminer les coordonnées des points \(\displaystyle E\) et \(\displaystyle F\) d'intersection de \(\displaystyle \mathcal{C}\) avec l'axe des abscisses.
Question 5 : Dire si le segment \(\displaystyle \left[EF\right]\) est un diamètre de \(\displaystyle \mathcal{C}\)
Correction de l'exercice n° 8-9 :
Question 1 : Pour obtenir la nature du triangle \(\displaystyle ABC\), on calcule les longueurs de chaque côtés :
Comme \(\displaystyle A\left(2;4\right)\) et \(\displaystyle B\left(-1;2\right)\) alors \(\displaystyle \overrightarrow{AB}\begin{pmatrix} -3 \\ -2\\ \end{pmatrix}\).
Comme \(\displaystyle A\left(2;4\right)\) et \(\displaystyle C\left(6;-2\right)\) alors \(\displaystyle \overrightarrow{AC}\begin{pmatrix} 4 \\ -6\\ \end{pmatrix}\).
Comme \(\displaystyle B\left(-1;2\right)\) et \(\displaystyle C\left(6;-2\right)\) alors \(\displaystyle \overrightarrow{BC}\begin{pmatrix} 7 \\ -4\\ \end{pmatrix}\).
Les normes de chaque vecteur donnent :
\(\displaystyle \begin{align*} AB&=\left\|\overrightarrow{AB}\right\| & AC&=\left\|\overrightarrow{AC}\right\| & BC&=\left\|\overrightarrow{BC}\right\|\\ AB&=\sqrt{(-3)^2+(-2)^2} & AC&=\sqrt{4^2+(-6)^2} & BC&=\sqrt{7^2+(-4)^2} \\ AB&=\sqrt{9+4} & AC&=\sqrt{16+36} & BC&=\sqrt{49+16}\\ AB&=\sqrt{13} & AC&=\sqrt{52} & BC&=\sqrt{65} \\ \end{align*} \)
On remarque que \(\displaystyle AB\neq AC \neq BC\) donc le triangle est ni équilatéral, ni isocèle. On procède ensuite aux deux calculs suivants :
\(\displaystyle \begin{align*} \text{On a d'une part } AB^2+AC^2&=\left(\sqrt{13}\right)^2+\left(\sqrt{52}\right)^2 & \text{ et d'autre part } BC^2&=\left(\sqrt{65}\right)^2 \\ AB^2+AC^2&=13+52 & BC^2&=65 \\ AB^2+AC^2&=65 & & \end{align*} \)
On remarque que \(\displaystyle AB^2+AC^2=BC^2\) donc d'après la réciproque du théorème de Pythagore, le triangle est rectangle.
Question 2 : Le cercle \(\displaystyle \mathcal{C}\) est circonscrit au triangle. Comme ce dernier est rectangle, alors l'hypoténuse \(\displaystyle \left[BC\right]\) représente le rayon du cercle circonscrit. Les coordonnées de son centre sont celles du milieu du segment \(\displaystyle \left[BC\right]\). Posons \(\displaystyle I\) ce point :
Comme \(\displaystyle B\left(-1;2\right)\) et \(\displaystyle C\left(6;-2\right)\) alors \(\displaystyle I\left(\dfrac{-1+6}{2};\dfrac{2-2}{2}\right)\), soit finalement \(\displaystyle I\left(\dfrac{5}{2};0\right)\).
Le centre du cercle est le point \(\displaystyle I\left(\dfrac{5}{2};0\right)\). Son rayon se calcule par la distance \(\displaystyle IB\) :
Comme \(\displaystyle I\left(\dfrac{5}{2};0\right)\) et \(\displaystyle B\left(-1;2\right)\) alors \(\displaystyle \overrightarrow{IB}\begin{pmatrix} \dfrac{-7}{2} \\ 2\\ \end{pmatrix}\).
La norme donne :
\(\displaystyle \begin{align*} IB&=\left\|\overrightarrow{IB}\right\| \\ IB&=\sqrt{\left(\dfrac{-7}{2}\right)^2+2^2} \\ IB&=\sqrt{\dfrac{49}{4}+4} \\ IB&=\sqrt{\dfrac{65}{4}} \\ \end{align*} \)
Le rayon du cercle est de \(\displaystyle \dfrac{\sqrt{65}}{2}\).
Question 3 : Si le point \(\displaystyle D\left(3;-4\right)\) appartient au cercle \(\displaystyle \mathcal{C}\) alors on doit avoir \(\displaystyle ID=\dfrac{\sqrt{65}}{2}\)
Comme \(\displaystyle I\left(\dfrac{5}{2};0\right)\) et \(\displaystyle D\left(3;-4\right)\) alors \(\displaystyle \overrightarrow{ID}\begin{pmatrix} \dfrac{1}{2} \\ -4\\ \end{pmatrix}\).
La norme donne :
\(\displaystyle \begin{align*} ID&=\left\|\overrightarrow{ID}\right\| \\ ID&=\sqrt{\left(\dfrac{1}{2}\right)^2+(-4)^2} \\ ID&=\sqrt{\dfrac{1}{4}+16} \\ ID&=\sqrt{\dfrac{65}{4}} \\ \end{align*} \)
On arrive bien à \(\displaystyle ID=\dfrac{\sqrt{65}}{2}\) donc le point \(\displaystyle D\) appartient bien au cercle.
Question 4 : Les points \(\displaystyle E\) et \(\displaystyle F\) ont pour ordonnée 0 car ils représentent les points d'intersection avec le cercle et l'axe des abscisses. On a alors \(\displaystyle E\left(x_E;0\right)\) et \(\displaystyle F\left(x_F;0\right)\).
Posons \(\displaystyle M\left(x;0\right)\) ce point d'intersection. La distance \(\displaystyle IM\) se calcule donc de la façon suivante :
Comme \(\displaystyle I\left(\dfrac{5}{2};0\right)\) et \(\displaystyle M\left(x;0\right)\) alors \(\displaystyle \overrightarrow{IM}\begin{pmatrix} x-\dfrac{5}{2} \\ 0\\ \end{pmatrix}\).
Ensuite, on calcule la distance au carré pour anticiper et obtenir les deux valeurs de \(\displaystyle x\) : \(\displaystyle \begin{align*} IM^2&=\left\|\overrightarrow{IM}\right\|^2 \\ IM^2&=\sqrt{\left(x-\dfrac{5}{2}\right)^2+0^2}^2 \\ IM^2&=\sqrt{\left(x-\dfrac{5}{2}\right)^2}^2 \\ IM^2&=\left(x-\dfrac{5}{2}\right)^2 \\ \end{align*} \)
Or, comme le rayon du cercle est de \(\displaystyle \dfrac{\sqrt{65}}{2}\), alors on doit donc avoir \(\displaystyle \left(x-\dfrac{5}{2}\right)^2=\left(\dfrac{\sqrt{65}}{2}\right)^2\) :
\(\displaystyle \begin{align*} \left(x-\dfrac{5}{2}\right)^2&=\left(\dfrac{\sqrt{65}}{2}\right)^2 \\ \left(x-\dfrac{5}{2}\right)^2-\dfrac{65}{4}&=0 \\ \left(x-\dfrac{5}{2}-\dfrac{\sqrt{65}}{2}\right)\left(x-\dfrac{5}{2}+\dfrac{\sqrt{65}}{2}\right)&=0 \\ \left(x-\dfrac{5+\sqrt{65}}{2}\right)\left(x-\dfrac{5-\sqrt{65}}{2}\right)&=0 \\ \end{align*} \)
Un produit de facteurs est nul si au moins l'un d'eux est nul :
\(\displaystyle \begin{align*} \text{On a d'une part } x-\dfrac{5+\sqrt{65}}{2}&=0 & \text{ et d'autre part } x-\dfrac{5-\sqrt{65}}{2}&=0 \\ x&=\dfrac{5+\sqrt{65}}{2} & x&=\dfrac{5-\sqrt{65}}{2} \\ \end{align*} \)
Les coordonnées des deux points sont donc \(\displaystyle E\left(\dfrac{5+\sqrt{65}}{2};0\right)\) et \(\displaystyle F\left(\dfrac{5-\sqrt{65}}{2};0\right)\)
Question 5 : Le segment \(\displaystyle \left[EF\right]\) est un diamètre de \(\displaystyle \mathcal{C}\) si \(\displaystyle EF=2\times\dfrac{\sqrt{65}}{2}\).
Comme \(\displaystyle E\left(\dfrac{5-\sqrt{65}}{2};0\right)\) et \(\displaystyle F\left(\dfrac{5+\sqrt{65}}{2};0\right)\) alors \(\displaystyle \overrightarrow{EF}\begin{pmatrix} \dfrac{5+\sqrt{65}}{2}-\dfrac{5-\sqrt{65}}{2} \\ 0\\ \end{pmatrix}\), soit encore \(\displaystyle \overrightarrow{EF}\begin{pmatrix} \sqrt{65} \\ 0\\ \end{pmatrix}\)
La norme se calcule par : \(\displaystyle \begin{align*} EF&=\left\|\overrightarrow{EF}\right\| \\ EF&=\sqrt{\sqrt{65}^2} \\ EF&=\sqrt{65} \\ \end{align*} \)
Conclusion : On arrive bien à \(\displaystyle EF=2\times\dfrac{\sqrt{65}}{2}\) donc le \(\displaystyle \left[EF\right]\) est bien un diamètre du cercle \(\displaystyle \mathcal{C}\).
Envoyer la proposition de travail
Lancer l'interactivité