Enoncé de l'exercice n° 8-1 : (Extrait : n°4 page 167 livre 2nde Hachette Education)
Dans un repère orthonormé, on considère les points suivants :
| \(\displaystyle A\left(-5;8\right)\) | \(\displaystyle B\left(6;5\right)\) | \(\displaystyle C\left(-1;3\right)\) | \(\displaystyle D\left(3;2\right)\) | \(\displaystyle E\left(7;-7\right)\) |
Question 1 : Les points \(\displaystyle A\), \(\displaystyle C\) et \(\displaystyle E\) sont-ils alignés ?
Question 2 : Les droites \(\displaystyle \left(AB\right)\) et \(\displaystyle \left(CD\right)\) sont-elles parallèles ?
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 8-2 : (Extrait : n°5 page 167 livre 2nde Hachette Education)
Dans un repère orthonormé, on considère les points suivants :
| \(\displaystyle A\left(2;6\right)\) | \(\displaystyle B\left(-3;5\right)\) | \(\displaystyle C\left(4;1\right)\) | \(\displaystyle D\left(-8;-1\right)\) | \(\displaystyle E\left(6;-4\right)\) |
Question 1 : Les points \(\displaystyle A\), \(\displaystyle C\) et \(\displaystyle E\) sont-ils alignés ?
Question 2 : Les droites \(\displaystyle \left(AB\right)\) et \(\displaystyle \left(CD\right)\) sont-elles parallèles ?
Question 3 : Le triangle \(\displaystyle BCD\) est-il isocèle ?
Envoyer la proposition de travail
Lancer l'interactivité
On considère les points \(\displaystyle A\left(2;3\right)\) , \(\displaystyle B\left(1;-1\right)\) et \(\displaystyle C\left(6;2\right)\)
Question 1 : Démontrer que le triangle \(\displaystyle ABC\) est rectangle et isocèle.
Question 2 : Calculer les coordonnées du point \(\displaystyle D\) tel que \(\displaystyle ABCD\) soit un carré.
Envoyer la proposition de travail
Lancer l'interactivité
On considère les points \(\displaystyle A\left(-1;4\right)\) , \(\displaystyle B\left(5;2\right)\) et \(\displaystyle M\left(x;y\right)\).
Question 1 : Calculer les coordonnées du milieu \(\displaystyle I\) de \(\displaystyle \left[AB\right]\).
Question 2 : Exprimer les coordonnées de \(\displaystyle \overrightarrow{MA}\), \(\displaystyle \overrightarrow{MB}\) et \(\displaystyle \overrightarrow{MI}\) en fonction de \(\displaystyle x\) et de \(\displaystyle y\).
Question 3 : Démontrer que \(\displaystyle \overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\).
Envoyer la proposition de travail
Lancer l'interactivité
On considère les points \(\displaystyle A\left(-2;5\right)\) , \(\displaystyle B\left(2;-2\right)\) et \(\displaystyle C\left(6;3\right)\).
Question 1 : Déterminer les coordonnées du point \(\displaystyle D\), défini par \(\displaystyle \overrightarrow{AD}=\frac{3}{2}\overrightarrow{AC}\).
Question 2 : Déterminer les coordonnées du point \(\displaystyle E\), défini par \(\displaystyle \overrightarrow{BE}=\frac{-1}{8}\overrightarrow{BA}+\frac{3}{8}\overrightarrow{BC}\).
Question 3 : Démontrer que les points \(\displaystyle B\), \(\displaystyle D\) et \(\displaystyle E\) sont alignés.
Envoyer la proposition de travail
Lancer l'interactivité
On considère les points \(\displaystyle A\left(-2;-3\right)\) , \(\displaystyle B\left(3;3\right)\) et \(\displaystyle C\left(4;-1\right)\). L'origine du repère est le point \(\displaystyle O\) et on note \(\displaystyle I\) le milieu de \(\displaystyle \left[AC\right]\).
Question 1 : Calculer les coordonnées du point \(\displaystyle P\), défini par \(\displaystyle \overrightarrow{OP}=\overrightarrow{OA}-2\overrightarrow{OB}+\overrightarrow{OC}\).
Question 2 : Démontrer que les droites \(\displaystyle \left(OP\right)\) et \(\displaystyle \left(IB\right)\) sont parallèles.
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 8-7 : (Extrait : Exercice n°64 page 175 Déclic 2nde Hachette)
Dans un repère orthonormé \(\displaystyle \left(O;I;J\right)\) on considère les points \(\displaystyle A\left(-4;2\right)\), \(\displaystyle B\left(4;-6\right)\), \(\displaystyle C\left(8;6\right)\), \(\displaystyle D\left(3;1\right)\) et \(\displaystyle E\left(0;-2\right)\)
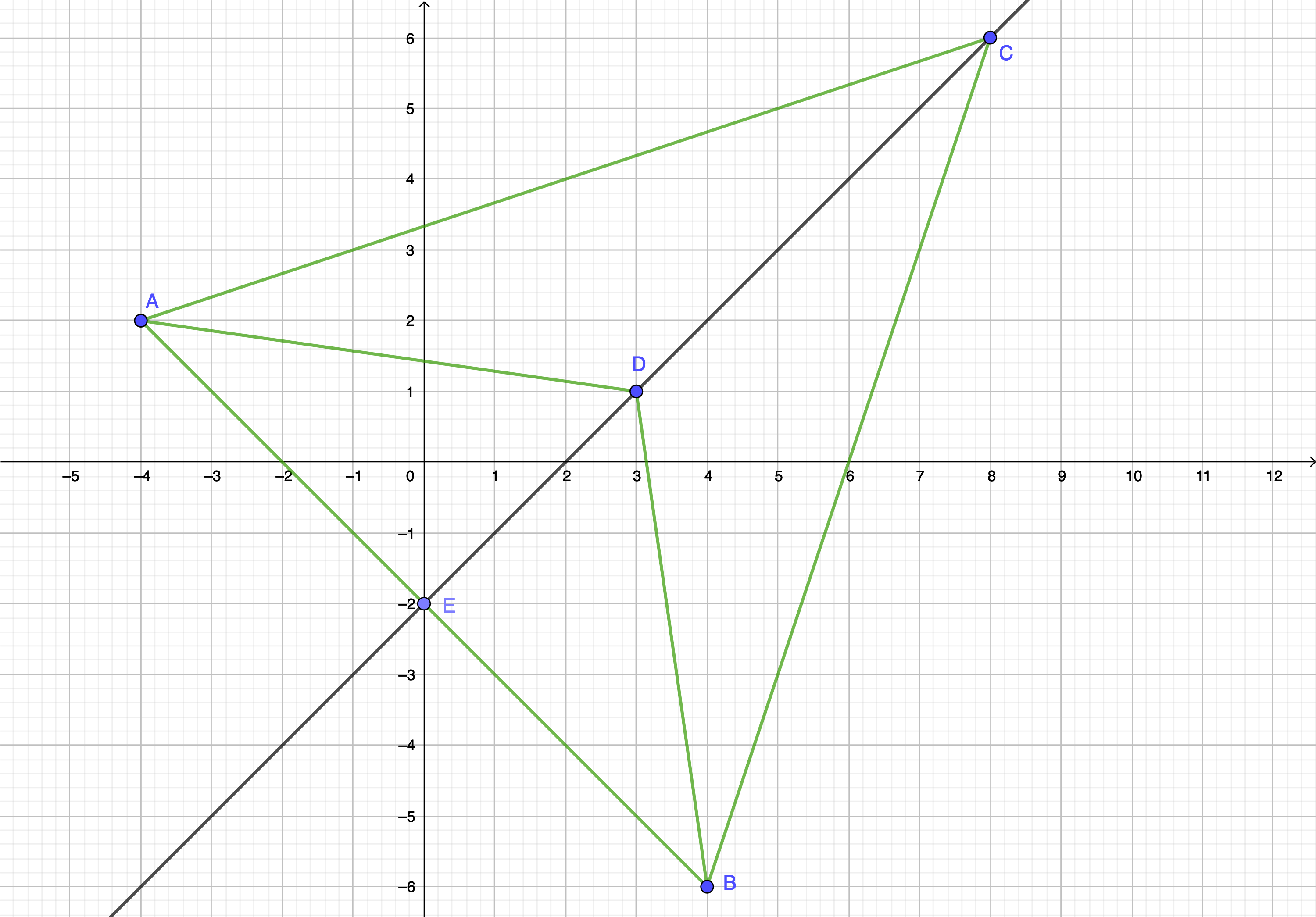
Question 1 : Montrer que le point \(\displaystyle D\) appartient à la médiatrice du segment \(\displaystyle \left[AB\right]\).
Question 2 : Déterminer la nature du triangle \(\displaystyle ABC\).
Question 3 : En déduire que \(\displaystyle \left(AB\right)\) et \(\displaystyle \left(CD\right)\) sont perpendiculaires.
Question 4 : Le point \(\displaystyle D\) est-il le milieu du segment \(\displaystyle \left[CE\right]\) ?
Question 5 : Calculer l'aire du triangle \(\displaystyle ABC\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 8-8 : (Extrait : Exercice n°84 page 178 Déclic 2nde Hachette)
Dans un repère orthonormé \(\displaystyle \left(O;I;J\right)\) on considère les points \(\displaystyle O\left(4;4\right)\), \(\displaystyle A\left(-1;4\right)\), \(\displaystyle B\left(8;7\right)\), \(\displaystyle C\left(0;1\right)\) , \(\displaystyle D\left(7;0\right)\) , \(\displaystyle T\left(1;8\right)\) et \(\displaystyle M\left(-7;2\right)\). La situation est résumée dans le schéma suivant :
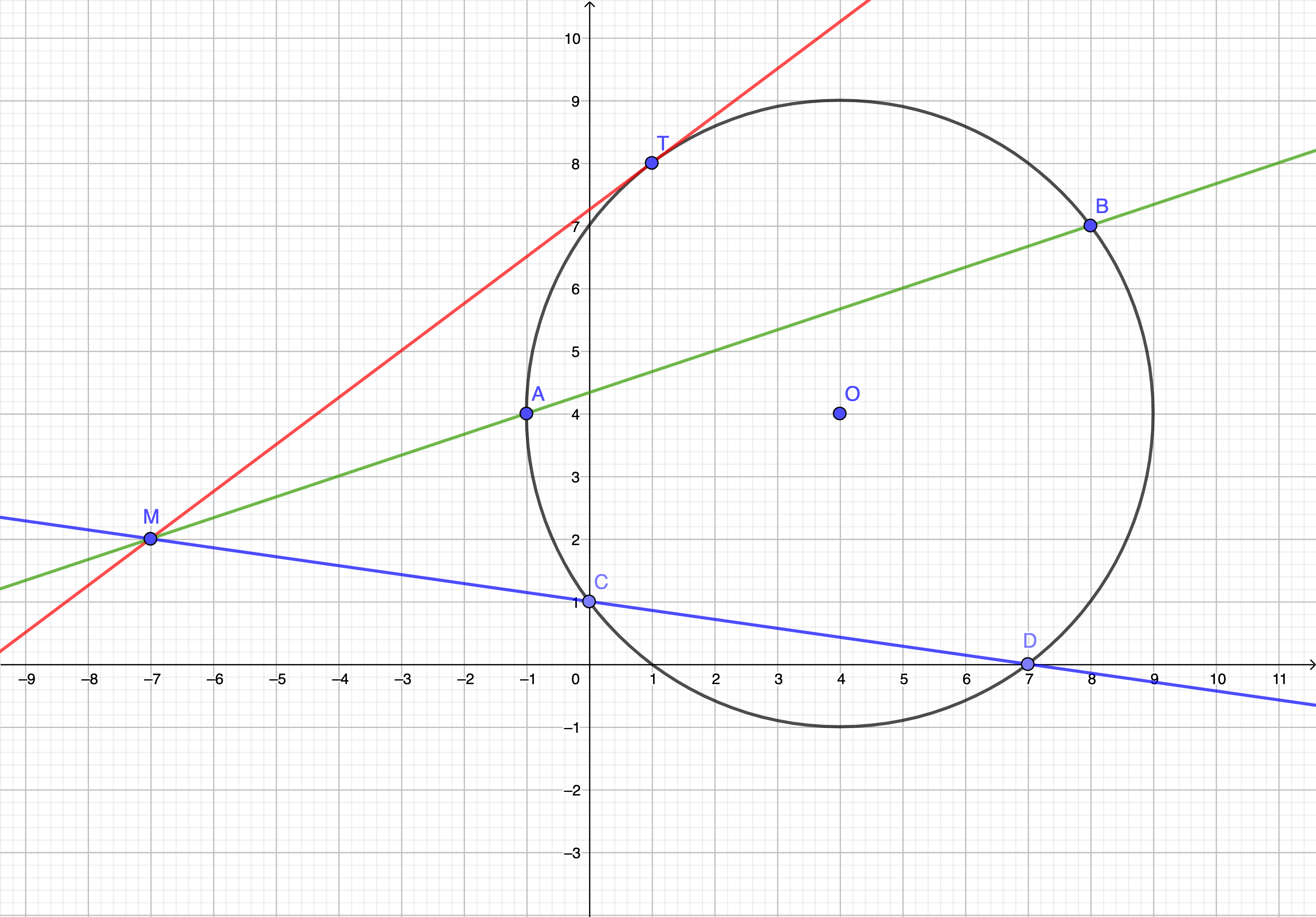
Question 1 : Justifier que les points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) et \(\displaystyle T\) appartiennent à un même cercle \(\displaystyle \mathcal{C}\) de centre \(\displaystyle O\).
Question 2 : Les points \(\displaystyle M\), \(\displaystyle A\) et \(\displaystyle B\) sont-ils alignés ?
Question 3 : Les points \(\displaystyle M\), \(\displaystyle C\) et \(\displaystyle D\) sont-ils alignés ?
Question 4 : Comparer les produits : \(\displaystyle MA\times MB\) ; \(\displaystyle MC\times MD\) et \(\displaystyle MT^2\).
Correction de l'exercice n° 8-8 :
Question 1 : Pour montrer que les points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) et \(\displaystyle T\) sont cocycliques, on montre que leur disance au point \(\displaystyle O\) est la même.
Comme \(\displaystyle O\left(4;4\right)\) et \(\displaystyle A\left(-1;4\right)\) alors \(\displaystyle \overrightarrow{OA}\begin{pmatrix} -5 \\ 0\\ \end{pmatrix}\).
Comme \(\displaystyle O\left(4;4\right)\) et \(\displaystyle B\left(8;7\right)\) alors \(\displaystyle \overrightarrow{OB}\begin{pmatrix} 4 \\ 3\\ \end{pmatrix}\).
Comme \(\displaystyle O\left(4;4\right)\) et \(\displaystyle C\left(0;1\right)\) alors \(\displaystyle \overrightarrow{OC}\begin{pmatrix} -4 \\ -3\\ \end{pmatrix}\).
Comme \(\displaystyle O\left(4;4\right)\) et \(\displaystyle D\left(7;0\right)\) alors \(\displaystyle \overrightarrow{OD}\begin{pmatrix} 3 \\ -4\\ \end{pmatrix}\).
Comme \(\displaystyle O\left(4;4\right)\) et \(\displaystyle T\left(1;8\right)\) alors \(\displaystyle \overrightarrow{OT}\begin{pmatrix} -3 \\ 4\\ \end{pmatrix}\).
Les normes de chaque vecteur donnent :
\(\displaystyle \begin{align*} OA&=\left\|\overrightarrow{OA}\right\| & OB&=\left\|\overrightarrow{OB}\right\| & OC&=\left\|\overrightarrow{OC}\right\|\\ OA&=\sqrt{(-5)^2+0^2} & OB&=\sqrt{4^2+3^2} & OC&=\sqrt{(-4)^2+(-3)^2} \\ OA&=\sqrt{25+0} & OB&=\sqrt{16+9} & OC&=\sqrt{16+9}\\ OA&=\sqrt{25} & OB&=\sqrt{25} & OC&=\sqrt{25} \\ OA&=5 & OB&=5 & OC&=5 \\ \end{align*} \)
\(\displaystyle \begin{align*} OD&=\left\|\overrightarrow{OD}\right\| & OT&=\left\|\overrightarrow{OT}\right\| \\ OD&=\sqrt{3^2+(-4)^2} & OT&=\sqrt{(-3)^2+4^2} \\ OD&=\sqrt{9+16} & OT&=\sqrt{9+16} \\ OD&=\sqrt{25} & OT&=\sqrt{25} \\ OD&=5 & OT&=5 \\ \end{align*} \)
Comme les distances au point \(\displaystyle O\) sont toutes les mêmes, on en conclut que les points sont cocycliques de centre \(\displaystyle O\) et de rayon 5.
Question 2 : Pour vérifier si les points sont alignés, on étudie la colinéarité des vecteurs \(\displaystyle \overrightarrow{MA}\) et \(\displaystyle \overrightarrow{MB}\) :
Comme \(\displaystyle M\left(-7;2\right)\) et \(\displaystyle A\left(-1;4\right)\) alors \(\displaystyle \overrightarrow{MA}\begin{pmatrix} 6 \\ 2\\ \end{pmatrix}\).
Comme \(\displaystyle M\left(-7;2\right)\) et \(\displaystyle B\left(8;7\right)\) alors \(\displaystyle \overrightarrow{MB}\begin{pmatrix} 15 \\ 5\\ \end{pmatrix}\).
On calcule ensuite leur déterminant :
\(\displaystyle \begin{align*} \det\left(\overrightarrow{MA};\overrightarrow{MB}\right)&=\begin{vmatrix} 6&15\\2&5\end{vmatrix} \\ &=-6\times5-2\times15 \\ &=30-30 \\ &=0 \end{align*} \)
Comme \(\displaystyle \det\left(\overrightarrow{MA};\overrightarrow{MB}\right)=0\) alors les vecteurs \(\displaystyle \overrightarrow{MA}\) et \(\displaystyle \overrightarrow{MB}\) sont colinéaires. Comme enfin ils ont un point en commun, alors les points \(\displaystyle M\), \(\displaystyle A\) et \(\displaystyle B\) sont alignés.
Question 3 : Pour vérifier si les points sont alignés, on étudie la colinéarité des vecteurs \(\displaystyle \overrightarrow{MC}\) et \(\displaystyle \overrightarrow{MD}\) :
Comme \(\displaystyle M\left(-7;2\right)\) et \(\displaystyle C\left(0;1\right)\) alors \(\displaystyle \overrightarrow{MC}\begin{pmatrix} 7 \\ -1\\ \end{pmatrix}\).
Comme \(\displaystyle M\left(-7;2\right)\) et \(\displaystyle D\left(7;0\right)\) alors \(\displaystyle \overrightarrow{MD}\begin{pmatrix} 14 \\ -2\\ \end{pmatrix}\).
On calcule ensuite leur déterminant :
\(\displaystyle \begin{align*} \det\left(\overrightarrow{MC};\overrightarrow{MD}\right)&=\begin{vmatrix} 7&14\\-1&-2\end{vmatrix} \\ &=-7\times (-2)-14\times (-1) \\ &=-14+14 \\ &=0 \end{align*} \)
Comme \(\displaystyle \det\left(\overrightarrow{MC};\overrightarrow{MD}\right)=0\) alors les vecteurs \(\displaystyle \overrightarrow{MC}\) et \(\displaystyle \overrightarrow{MD}\) sont colinéaires. Comme enfin ils ont un point en commun, alors les points \(\displaystyle M\), \(\displaystyle C\) et \(\displaystyle D\) sont alignés.
Question 4 : Pour comparer les produits, il faut les effectuer :
\(\displaystyle \begin{align*} MA\times MB&=\sqrt{6^2+2^2} \times \sqrt{15^2+5^2} & MC\times MD&=\sqrt{7^2+(-1)^2} \times \sqrt{14^2+(-2)^2} & MT^2&=\sqrt{(-8)^2+(-6)^2}^2 \\ MA\times MB&=\sqrt{36+4} \times \sqrt{225+25} & MC\times MD&=\sqrt{49+1} \times \sqrt{196+4} & MT^2&=\sqrt{64+36}^2 \\ MA\times MB&=\sqrt{40} \times \sqrt{250} & MC\times MD&=\sqrt{50} \times \sqrt{200} & MT^2&=\sqrt{100}^2 \\ MA\times MB&=\sqrt{40\times 250} & MC\times MD&=\sqrt{50\times 200} & MT^2&=1000 \\ MA\times MB&=100 & MC\times MD&=100 & MT^2&=100 \\ \end{align*} \)
On remarque que les valeurs des produits sont identiques.
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 8-9 : (Extrait : Exercice n°85 page 178 Déclic 2nde Hachette)
Dans un repère orthonormé \(\displaystyle \left(O;I;J\right)\) on considère les points \(\displaystyle A\left(2;4\right)\), \(\displaystyle B\left(-1;2\right)\) et \(\displaystyle C\left(6;-2\right)\).
On note \(\displaystyle \mathcal{C}\) le cercle circonscrit au triangle \(\displaystyle ABC\). La situation est résumée dans la figure suivante :
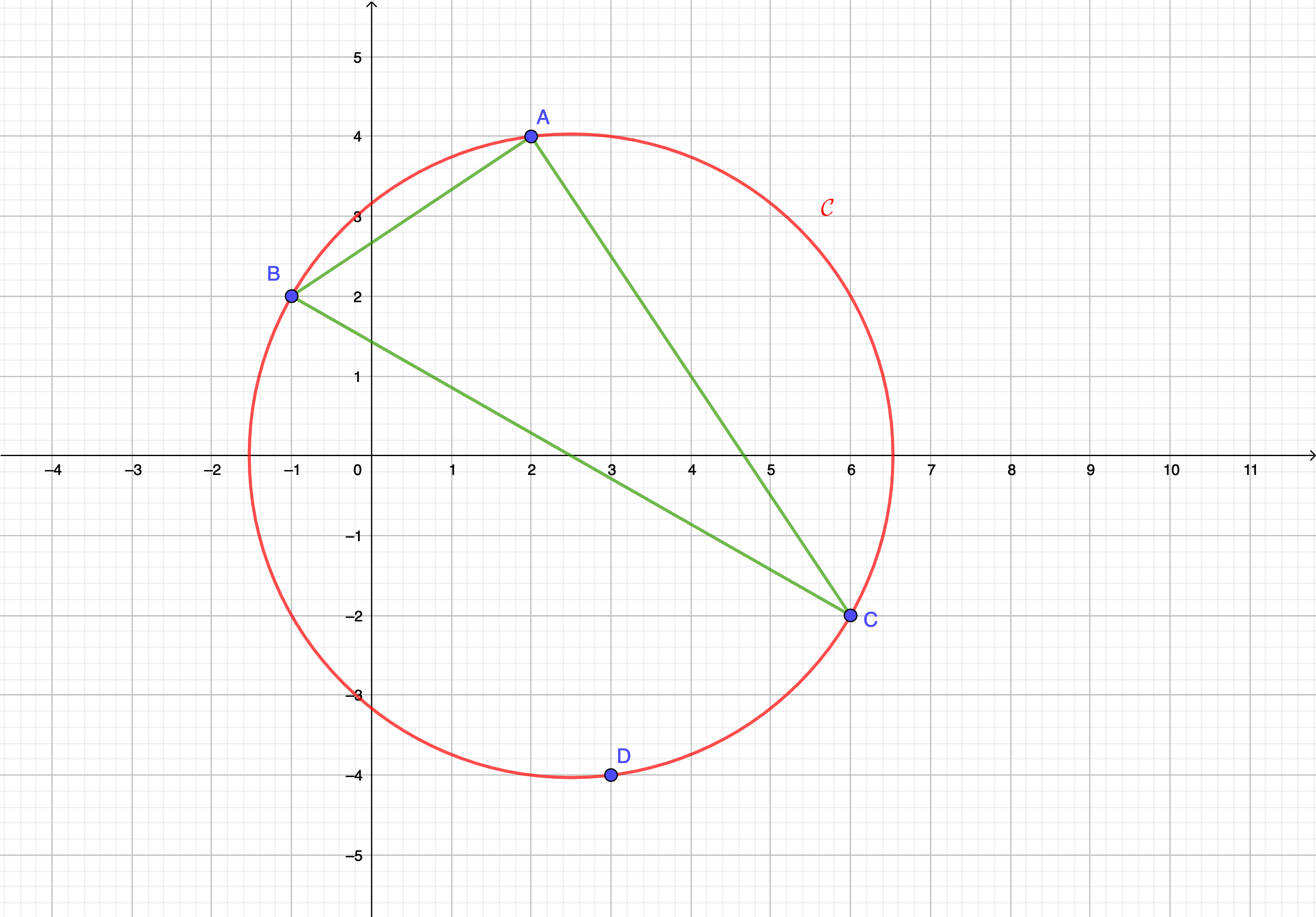
Question 1 : Donner la nature du triangle \(\displaystyle ABC\).
Question 2 : Déterminer le centre et le rayon du cercle \(\displaystyle \mathcal{C}\).
Question 3 : Justifier si le point \(\displaystyle D\left(3;-4\right)\) appartient au cercle \(\displaystyle \mathcal{C}\).
Question 4 : Déterminer les coordonnées des points \(\displaystyle E\) et \(\displaystyle F\) d'intersection de \(\displaystyle \mathcal{C}\) avec l'axe des abscisses.
Question 5 : Dire si le segment \(\displaystyle \left[EF\right]\) est un diamètre de \(\displaystyle \mathcal{C}\)
Envoyer la proposition de travail
Lancer l'interactivité