I) Mise en situation
En astrophysique, une loi stipule que l'aire balayée par une orbite de planète pendant une certaine durée, est la même, quelque soit la position autour de son étoile. La situation est schématisée de la façon suivante :
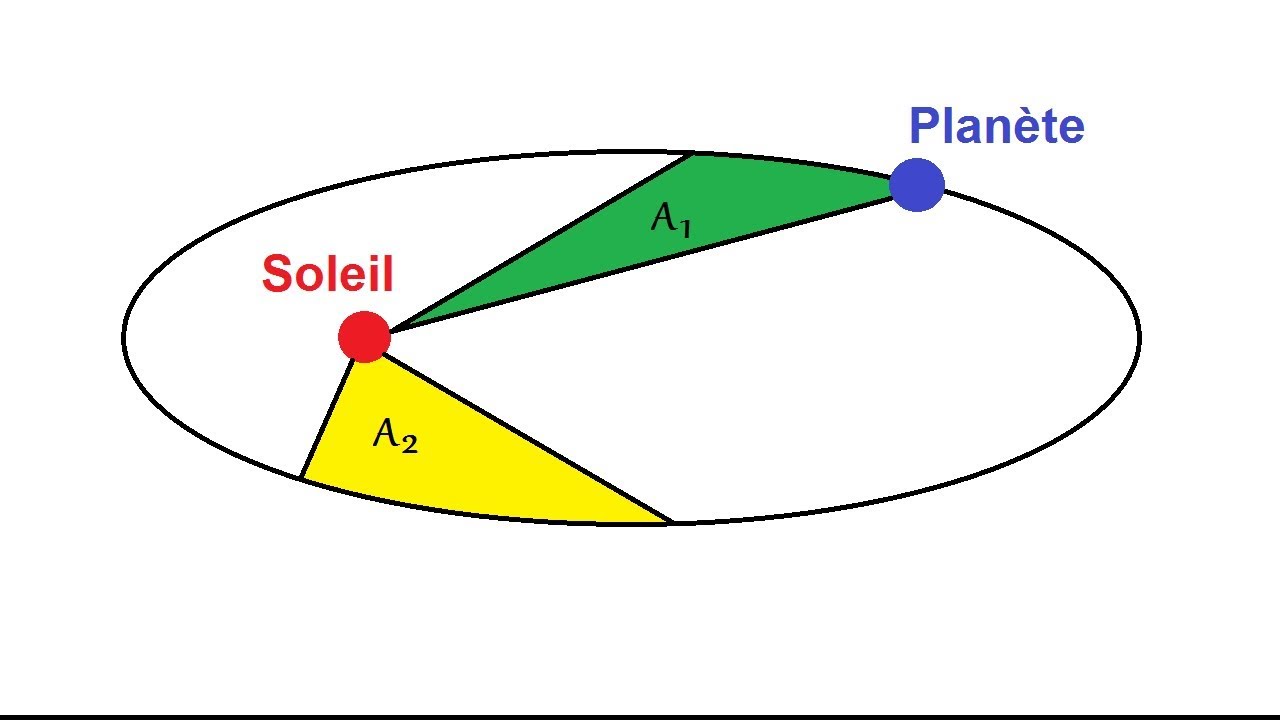
De cette loi, une troisième est donnée par le même physicien en enonçant que si \( \displaystyle r\) est le demi grand axe de l'ellipse (trajectoire de la planète) et \( \displaystyle T\) la période de rotation, on a alors quelque soit la planète, et pour toutes les planètes du système solaire, \( \displaystyle \frac{T^2}{r^3}=cte\).
On remarque alors que les notions de géométrie sont intimement liées à l'algèbre et en particulier aux expressions littérales.
Pour arriver à de telles lois, il est important de maîtriser les bases de la géométrie, apprises au collège et qui doivent être renforcées au lycée. Pour cela, on travaille sur une petite activité : activité n°4
II) Rappels des connaissances exigibles
On rappelle ici les principales notions de géométrie vues au collège.
1) Le théorème de Pyhagore
Le théorème de Pythagore se distingue en trois propriétés :
Propriété : (Théorème de Pythagore)
Dans un triangle \(\displaystyle ABC\) rectangle en \(\displaystyle A\), la longueur au carrée de l'hypoténuse est égale à la somme des longueurs au carrée des deux autres côtés. L'égalité s'écrit \(\displaystyle BC^2=AB^2+AC^2\).
Exemple : Confère la rédaction type en cliquant ici
Propriété : (Réciproque du théorème de Pythagore)
Dans un triangle \(\displaystyle ABC\) dont le plus grand côté est \(\displaystyle \left[BC\right]\), si la longueur au carrée de ce plus grand côté est égale à la somme des longueurs au carrée des deux autres côtés, alors le triangle est rectangle.
Exemple : Confère la rédaction type en cliquant ici
Propriété : (Contraposée du théorème de Pythagore)
Dans un triangle \(\displaystyle ABC\) dont le plus grand côté est \(\displaystyle \left[BC\right]\), si la longueur au carrée de ce plus grand côté n'est pas égale à la somme des longueurs au carrée des deux autres côtés, alors le triangle n'est pas rectangle.
Exemple : Confère la rédaction type en cliquant ici
2) Le théorème de Thalès
Le théorème de Thalès se distingue en trois propriétés :
Propriété : (Théorème de Thalès)
Si dans un triangle, une droite coupe deux côtés parallèlement au troisième côté, alors les deux triangles formés ont des côtés deux à deux proportionnels.
Ainsi, si dans un triangle \( \displaystyle ABC\), où \( \displaystyle B'\) est un point de \( \displaystyle \left(AB\right)\) et \( \displaystyle C'\) est un point de \( \displaystyle \left(AC\right)\), les droites \( \displaystyle \left(B'C'\right)\) et \( \displaystyle \left(BC\right)\) sont parallèles, alors \( \displaystyle \frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}\).
Exemple : Confère la rédaction type en cliquant ici
Propriété : (Réciproque du théorème de Thalès)
On considère deux droites \( \displaystyle d\) et \( \displaystyle d'\) sécantes en \( \displaystyle A\), deux points \( \displaystyle B\) et \( \displaystyle M\) de la droite \( \displaystyle d\) distincts de \( \displaystyle A\) et deux points \( \displaystyle C\) et \( \displaystyle N\) de la droite \( \displaystyle d'\), distincts de \( \displaystyle A\).
Alors Si \( \displaystyle \frac{AM}{AB}=\frac{AN}{AC} \), et si les points \( \displaystyle A \),\( \displaystyle B \),\( \displaystyle M \) et les points \( \displaystyle A \),\( \displaystyle C \),\( \displaystyle N \) sont alignés dans le même ordre, alors les droites \( \displaystyle (BC) \) et \( \displaystyle (MN) \) sont parallèles.
Exemple : Confère la rédaction type en cliquant ici
Propriété : (Conséquence (ou contraposée) du théorème de Thalès)
Si deux droites \( \displaystyle \left(BM\right)\) et \( \displaystyle \left(CN\right)\) sont sécantes en \( \displaystyle A\) et si deux des rapports \( \displaystyle \frac{AM}{AB}\), \( \displaystyle \frac{AN}{AC}\), \( \displaystyle \frac{MN}{BC}\) ne sont pas égaux, alors le sdroites \( \displaystyle \left(MN\right)\) et \( \displaystyle \left(BC\right)\) ne sont pas parallèles.
Exemple : Confère la rédaction type en cliquant ici
3) La trigonométrie
La trigonométrie auparavant étudiée est celle évoquée dans le triangle rectangle en introduisant la notion du cosinus, sinus et tangente d'un angle par les propriétés suivantes. Pour cela, nous partons du même schéma :
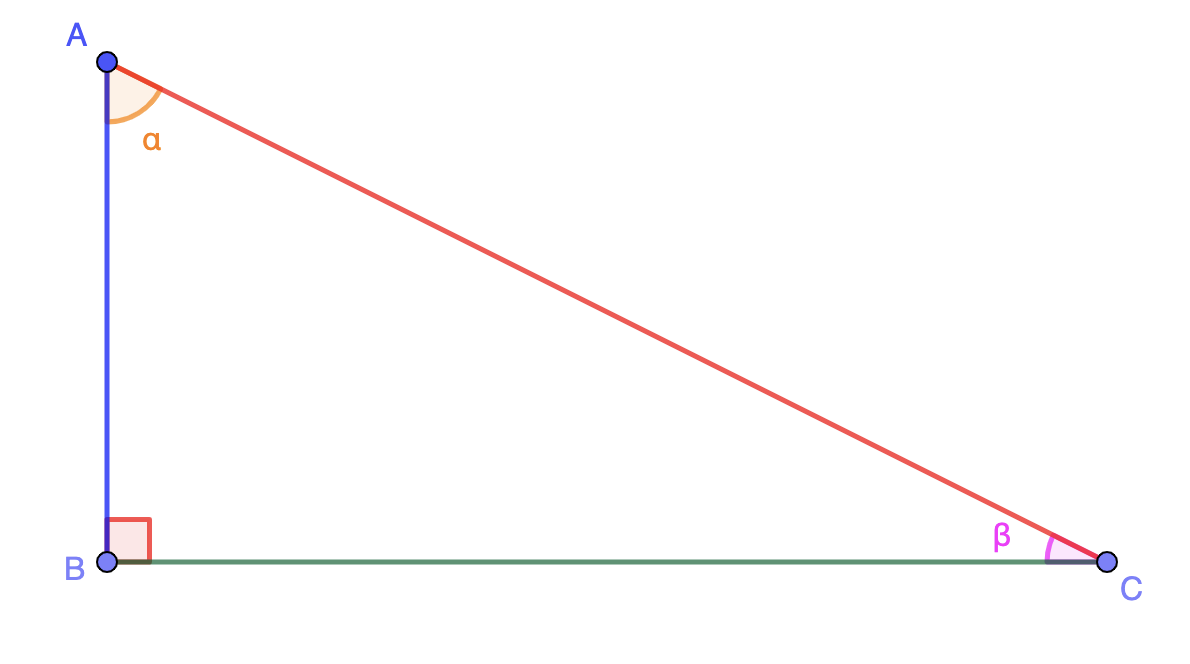
Propriété : Dans le triangle \( \displaystyle ABC \) rectangle en \( \displaystyle B\), le cosinus de l'angle \( \displaystyle \alpha\) est le rapport entre la longueur du côté adjacent à l'angle \( \displaystyle \alpha\) et l'hypoténuse. La formule se résume à \( \displaystyle \cos\left(\color{orange}{\alpha}\right)=\frac{\color{blue}{AB}}{\color{red}{AC}}\)
Exemple 1 : Confère la rédaction type en cliquant ici
Exemple 2 : Confère la rédaction type en cliquant ici
Propriété : Dans le triangle \( \displaystyle ABC \) rectangle en \( \displaystyle B\), le sinus de l'angle \( \displaystyle \alpha\) est le rapport entre la longueur du côté opposé à l'angle \( \displaystyle \alpha\) et l'hypoténuse. La formule se résume à \( \displaystyle \sin\left(\color{orange}{\alpha}\right)=\frac{\color{green}{BC}}{\color{red}{AC}}\)
Exemple 1 : Confère la rédaction type en cliquant ici
Exemple 2 : Confère la rédaction type en cliquant ici
Propriété : Dans le triangle \( \displaystyle ABC \) rectangle en \( \displaystyle B\), la tangente de l'angle \( \displaystyle \alpha\) est le rapport entre la longueur du côté opposé à l'angle \( \displaystyle \alpha\) et la longueur du côté adjacent à l'angle \( \displaystyle \alpha\). La formule se résume à \( \displaystyle \tan\left(\color{orange}{\alpha}\right)=\frac{\color{green}{BC}}{\color{blue}{AB}}\)
Exemple 1 : Confère la rédaction type en cliquant ici
Exemple 2 : Confère la rédaction type en cliquant ici
4) Autres rappels de propriétés avec les angles
Dans les schémas dans lesquelles il apparait des problèmes liés aux angles, il est utile de connaître les propriétés suivantes :
Propriété : Dans un triangle scalène, la somme des angles est de 180°.
Propriété : Lorsque deux droites sont parallèles, les angles alternes et internes sont égaux ; les angles au sommet sont égaux et les angles correspondants sont égaux.
Propriété : Lorsqu'un angle inscrit \( \displaystyle \alpha\) intercepte le même arc qu'un angle au centre \( \displaystyle \beta\), alors \( \displaystyle \beta=2\alpha \).
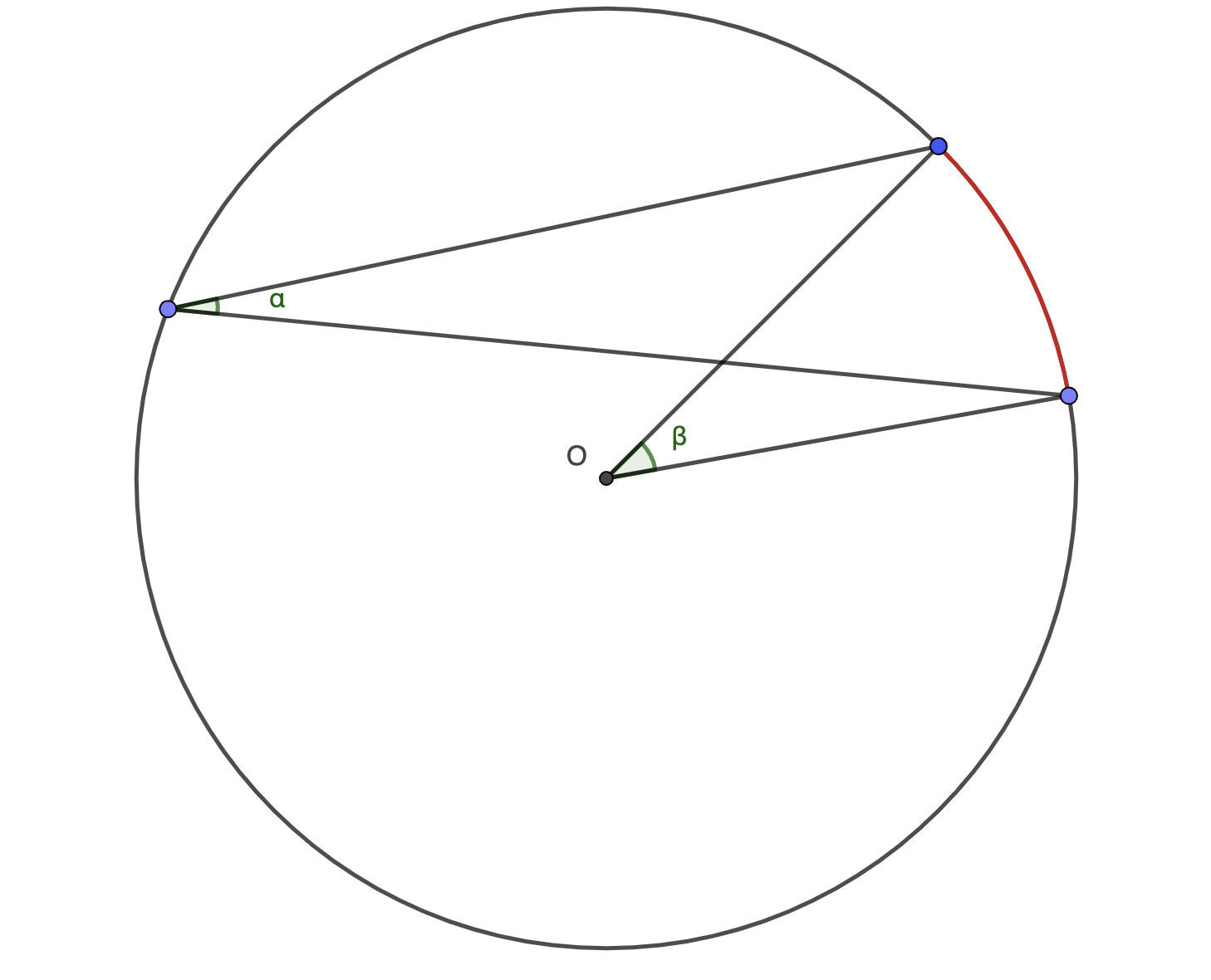
III) Le projeté orthogonal
On considère une droite \( \displaystyle \left(D\right)\) du plan et un point \( \displaystyle A\). On définit le projeté orthogonal de ce point de la façon suivante :
Définition : On appelle projeté orthogonal de \( \displaystyle A\) sur \( \displaystyle \left(D\right)\), le point d'intersection de la droite \( \displaystyle \left(D\right)\) avec la perpendiculaire à \( \displaystyle \left(D\right)\) passant par \( \displaystyle A\).
Propriété : La distance du point \( \displaystyle A\) à la droite \( \displaystyle \left(D\right)\) est la plus petite distance séparant un point de \( \displaystyle \left(D\right)\) avec \( \displaystyle A\). Elle est égale à \( \displaystyle AH\) où \( \displaystyle H\) est le projeté orthogonal du point \( \displaystyle A\) sur \( \displaystyle \left(D\right)\).
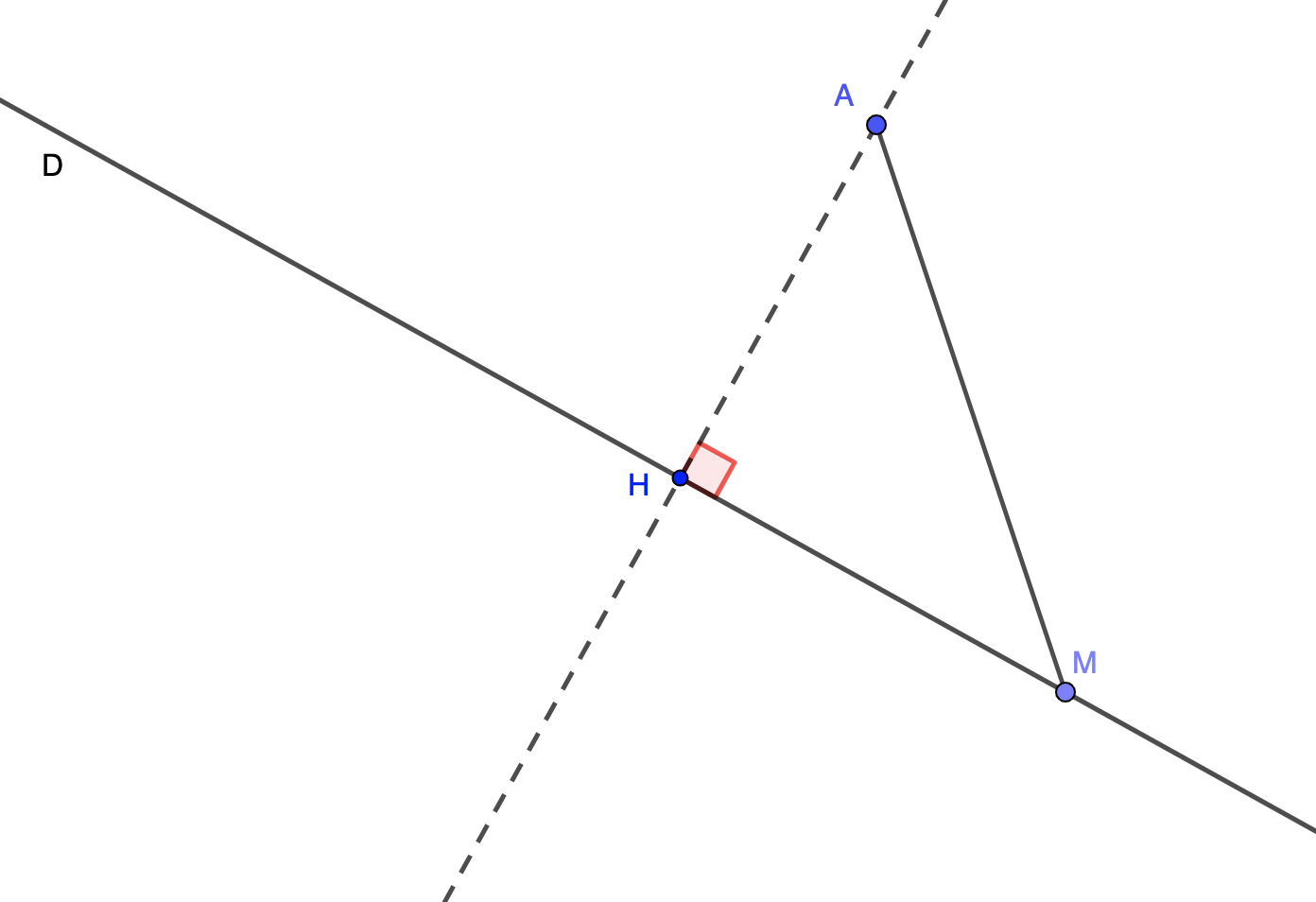
Démonstration à savoir :
Notons d la distance entre \( \displaystyle A\) et \( \displaystyle \left(D\right)\).
Soit \( \displaystyle M\) un point de \( \displaystyle \left(D\right)\), distinct de \( \displaystyle H\).
Le triangle \( \displaystyle AMH\) est rectangle en \( \displaystyle H\). Grâce au théorème de Pythagore, on peut affirmer que l'hypoténuse \( \displaystyle \left[AM\right]\) est le plus grand des côtés du triangle \( \displaystyle AMH\).
Donc \( \displaystyle AM > AH\).
Ainsi, la plus petite distance séparant \( \displaystyle A\) d'un point de \( \displaystyle \left(D\right)\) est égale à \( \displaystyle AH\). On en déduit que \( \displaystyle AH=d\).
IV) La tangente à un cercle
On définit la tangente de la façon suivnte :
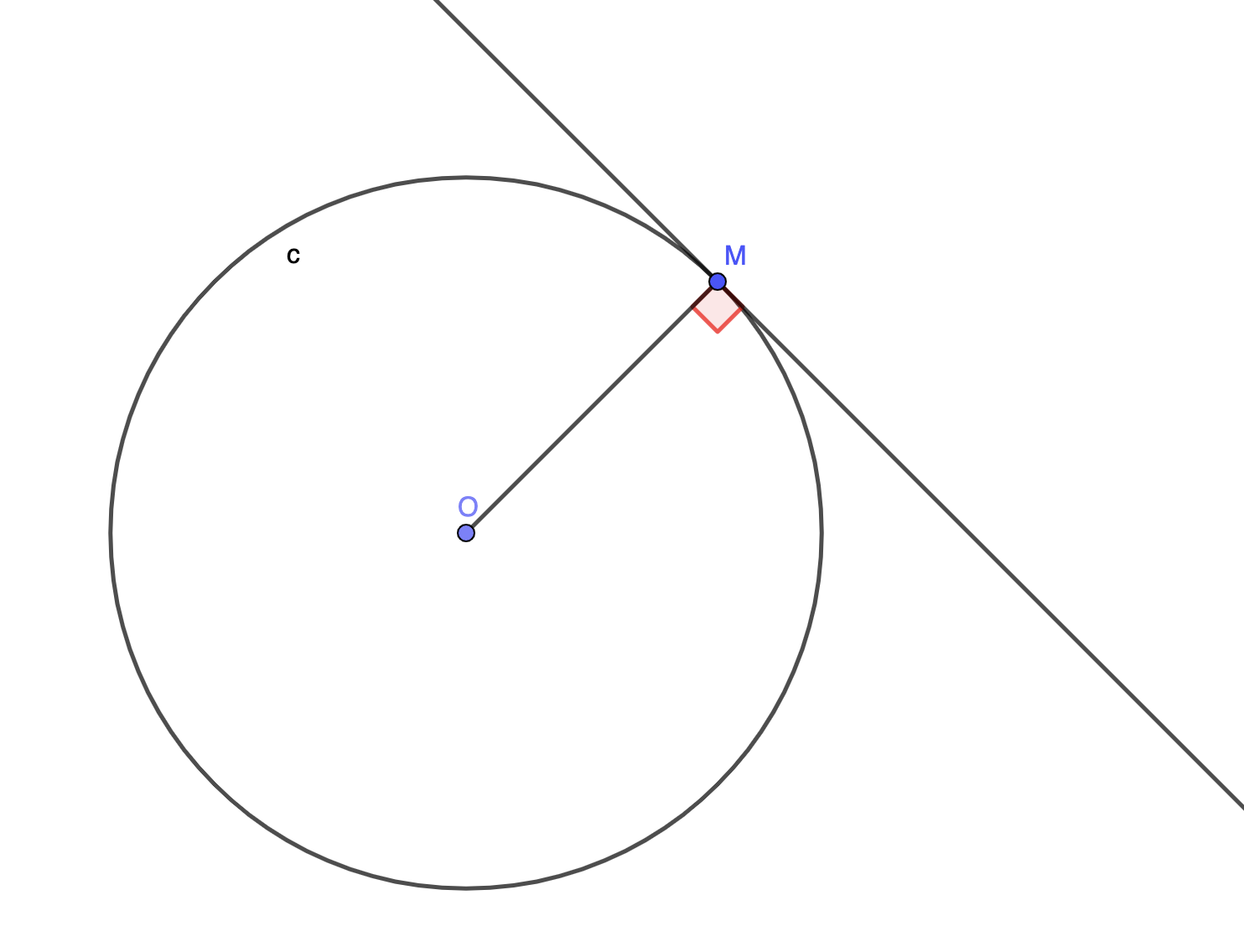
Définition : La tangente à un cercle \( \displaystyle \left(C\right)\) de centre \( \displaystyle O\) en un point \( \displaystyle M\) est la droite passant par \( \displaystyle M\) et perpendiculaire au rayon \( \displaystyle \left[OM\right]\). Elle coupe le cercle \( \displaystyle \left(C\right)\) en l'unique point \( \displaystyle M\).
V) Les droites remarquables dans un triangle
Dans un triangle scalène, on peut remarquer quatre types de droite :
1) Les trois hauteurs dans un triangle
La hauteur est définie de la façon suivante :
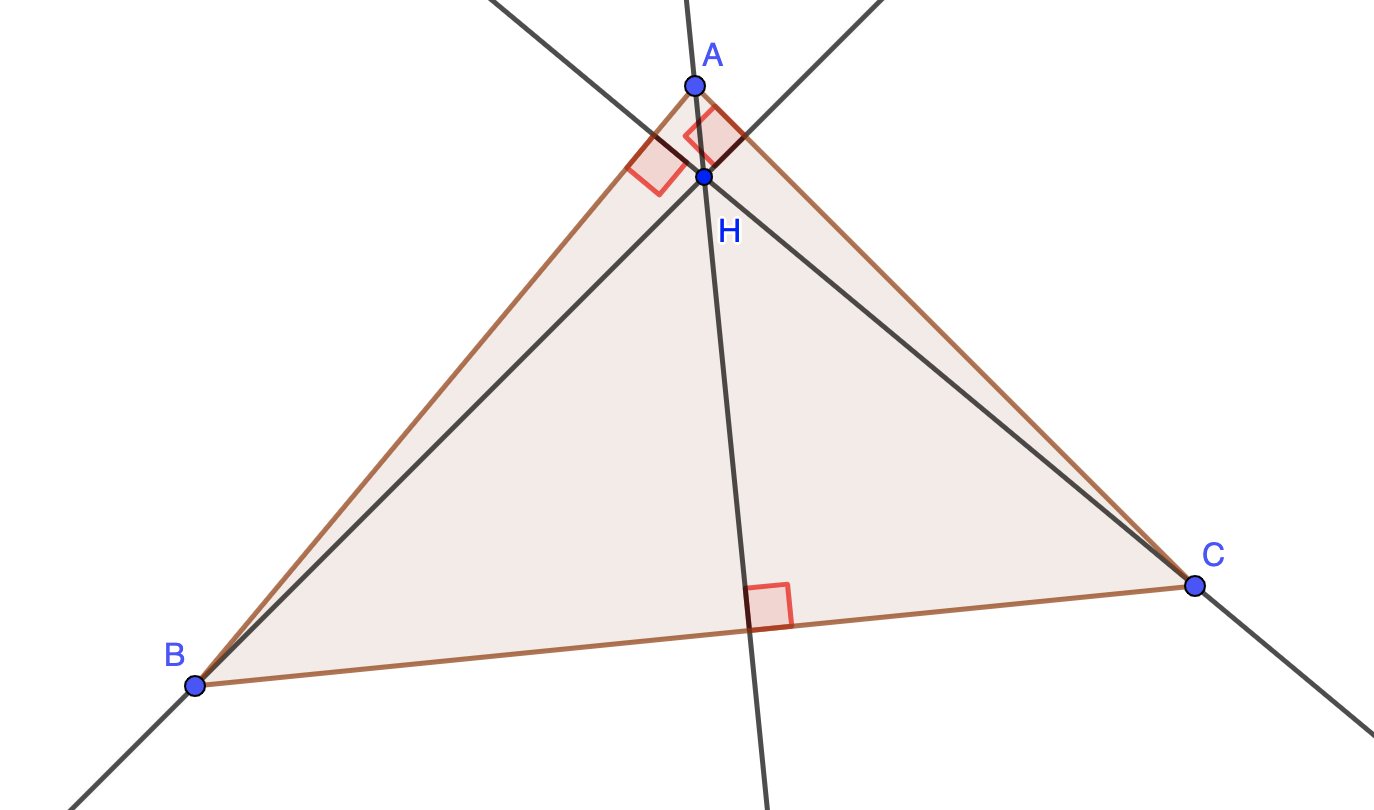
Définition : La hauteur dans un triangle est la droite, est une droite, issue d'un sommet, qui coupe perpendiculairement le côté opposé.
Propriété : Les trois hauteurs d'un triangle sont concourantes. Le point d'intersection est appelé l'orthocentre.
2) Les trois médianes dans un triangle
La médiane est définie de la façon suivante :
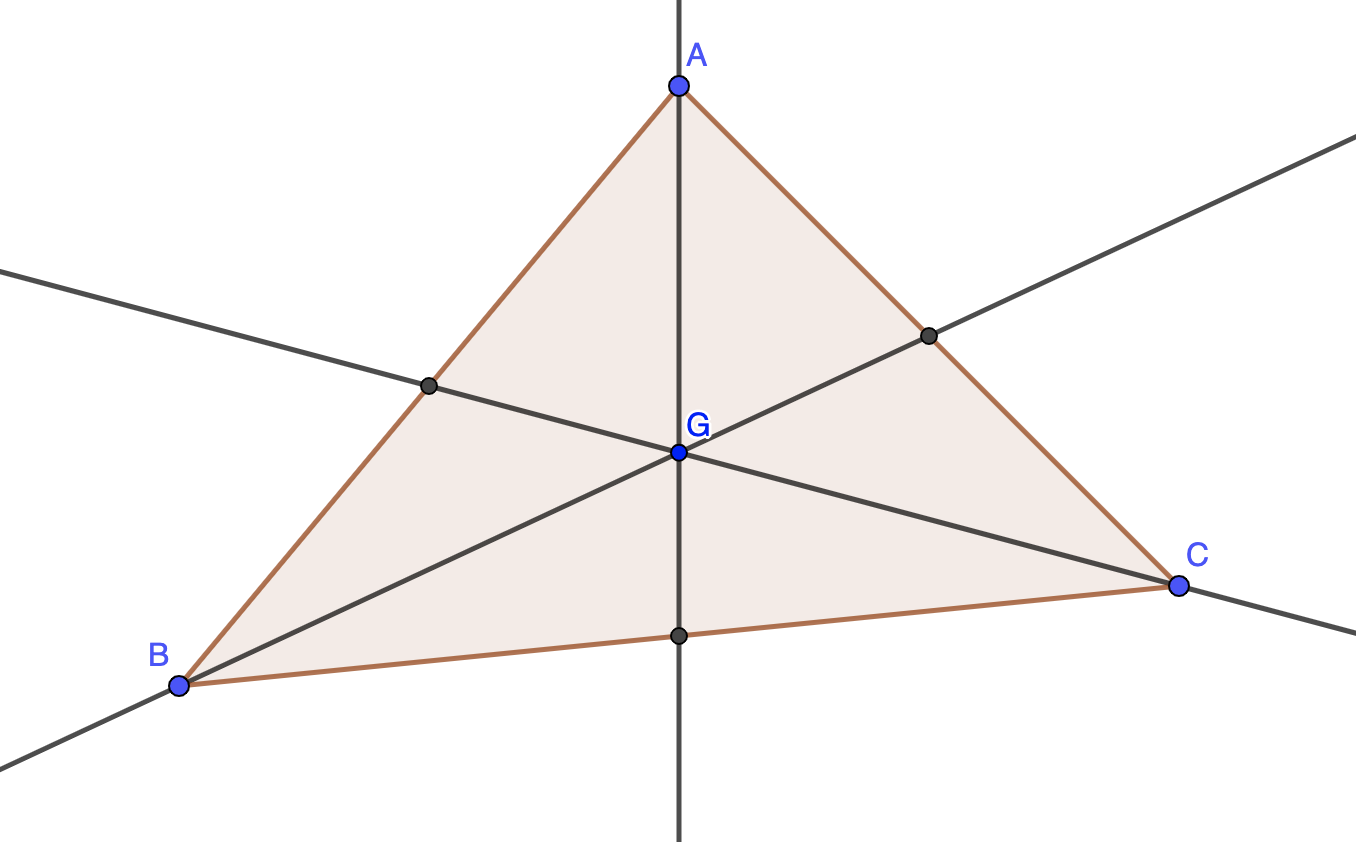
Définition : La médiane dans un triangle est une droite, issue d'un sommet, qui coupe le côté opposé en son milieu.
Propriété : Les trois médianes d'un triangle sont concourantes. Le point d'intersection est appelé le centre de gravité ou l'isobarycentre des points du triangle.
3) Les trois médiatrices dans un triangle
La médiatrice est définie de la façon suivante :
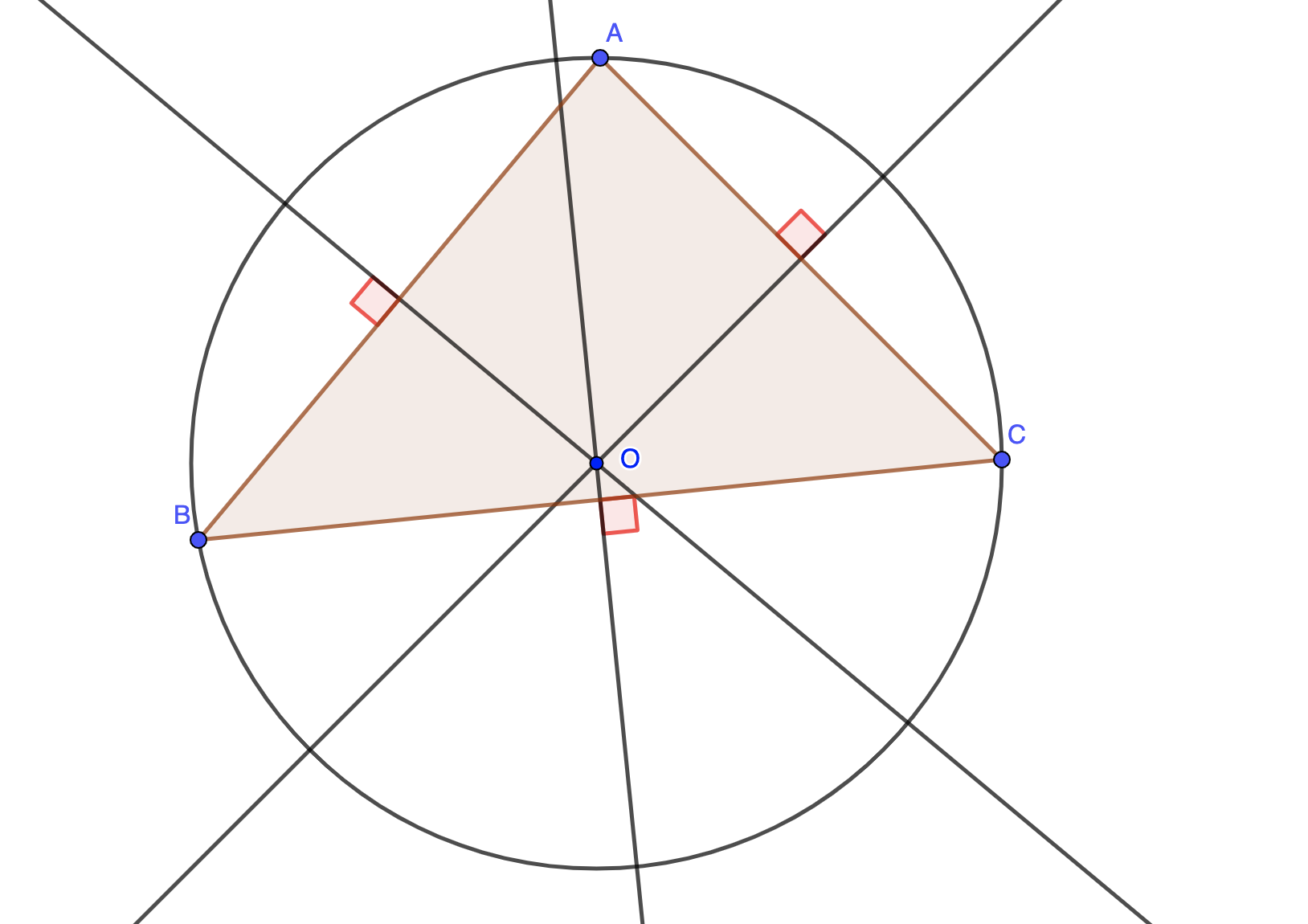
Définition : La médiatrice dans un triangle est une droite qui coupe perpendiculairement et en son milieu d'un des côtés.
Propriété : Les trois médiatrices d'un triangle sont concourantes. Le point d'intersection est appelé le centre du cercle circonscrit au triangle.
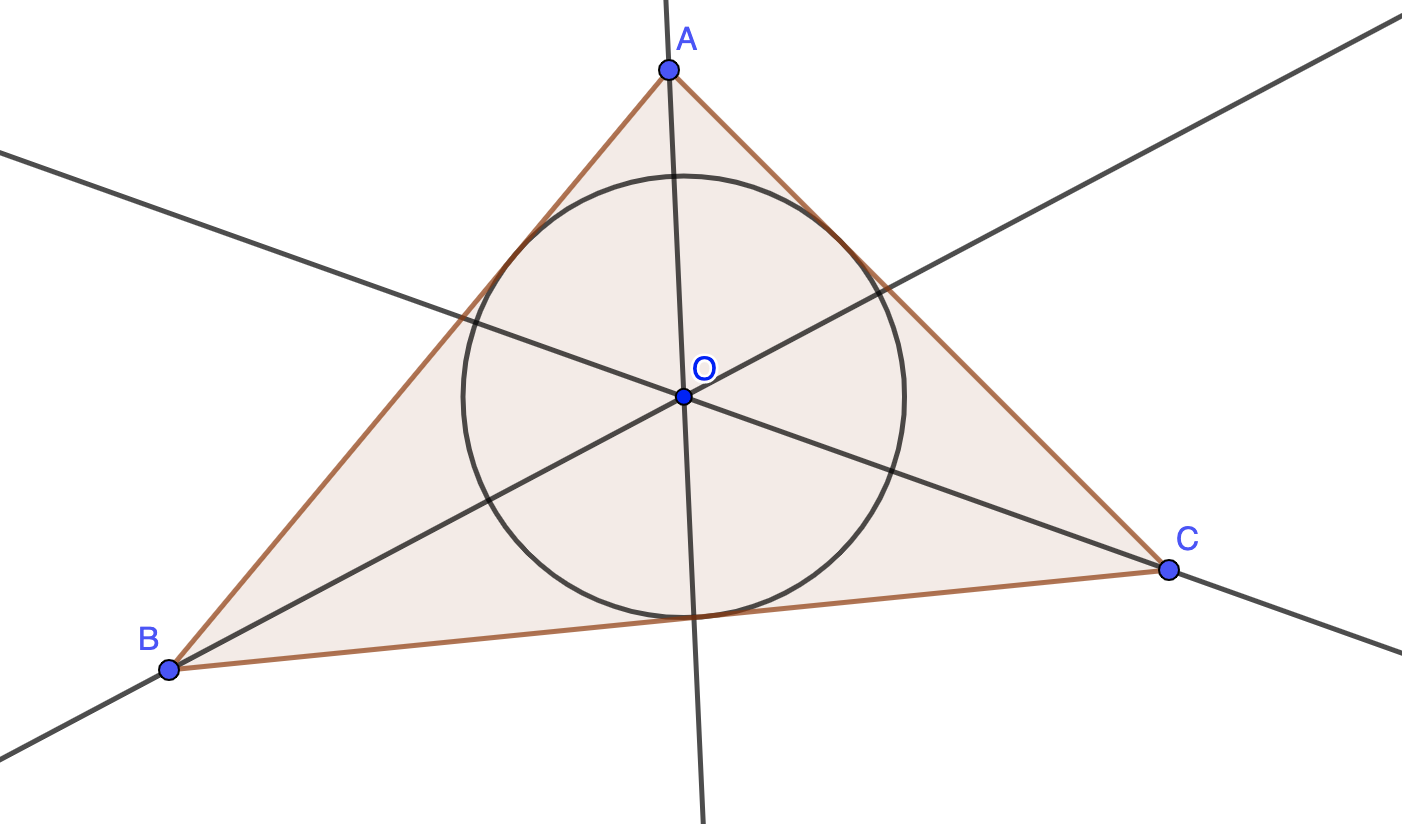
4) Les trois bissectrices dans un triangle
La bissectrice est définie de la façon suivante :
Définition : La bissectrice dans un triangle est une droite issue d'un sommet qui sépare le secteur angulaire de ce sommet en deux secteurs angulaires de même mesure.
Propriété : Les trois bissectrices d'un triangle sont concourantes. Le point d'intersection est appelé le centre du cercle inscrit au triangle.
VI) Complément de trigonométrie
Dans un triangle rectangle, schématisé dans la figure suivante, on peut donner une nouvelle propriété :

Propriété : Pour tout angle aigu \( \displaystyle \alpha\) dans un triangle rectangle, on a la relation trigonométrique \( \displaystyle \cos^2\left(\alpha\right)+\sin^2\left(\alpha\right)=1\).
Dans un triangle scalène, schématisé dans la figure suivante, on peut donner le théorème d'Al Kashi :
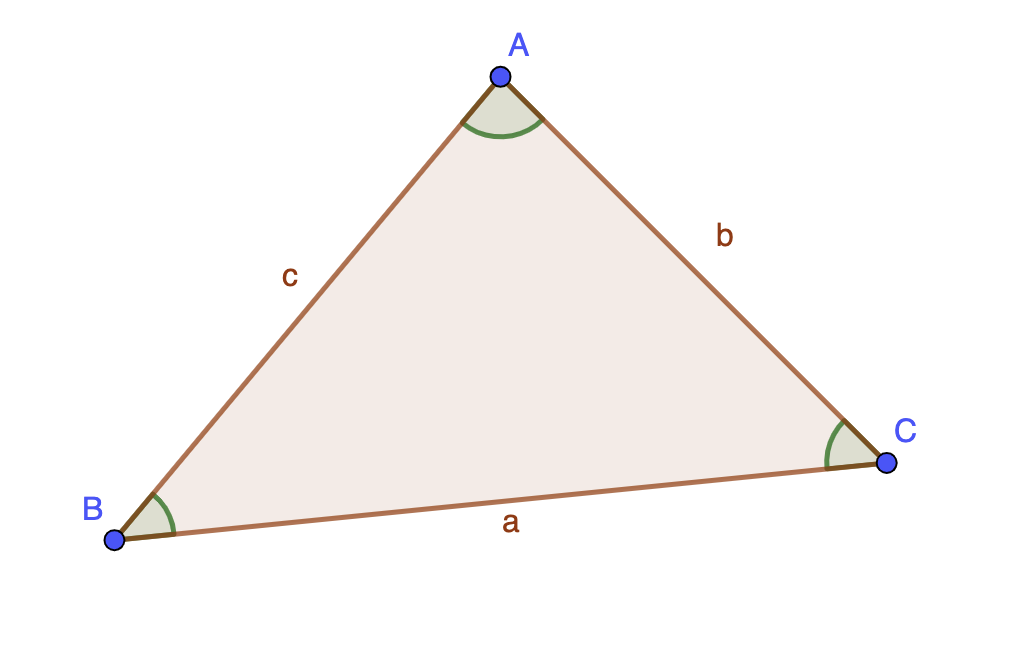
Propriété : Dans un triangle scalène \( \displaystyle ABC\) tel que \( \displaystyle AB=c\), \( \displaystyle AC=b\) et \( \displaystyle BC=a\), les trois relations d'Al-Kashi dans le triangle sont :
\( \displaystyle a^2=b^2+c^2-2bc\cos\left(\widehat{A}\right)\)
\( \displaystyle b^2=a^2+c^2-2ac\cos\left(\widehat{B}\right)\)
\( \displaystyle c^2=a^2+b^2-2ab\cos\left(\widehat{C}\right)\)