I) Mise en situation
Commençons par travailler sur l'activité suivante : activité n°6
Selon chaque génération, les types de télécommunication évoluent. Atcuellement, nous connaissons l'essort de la fibre optique.
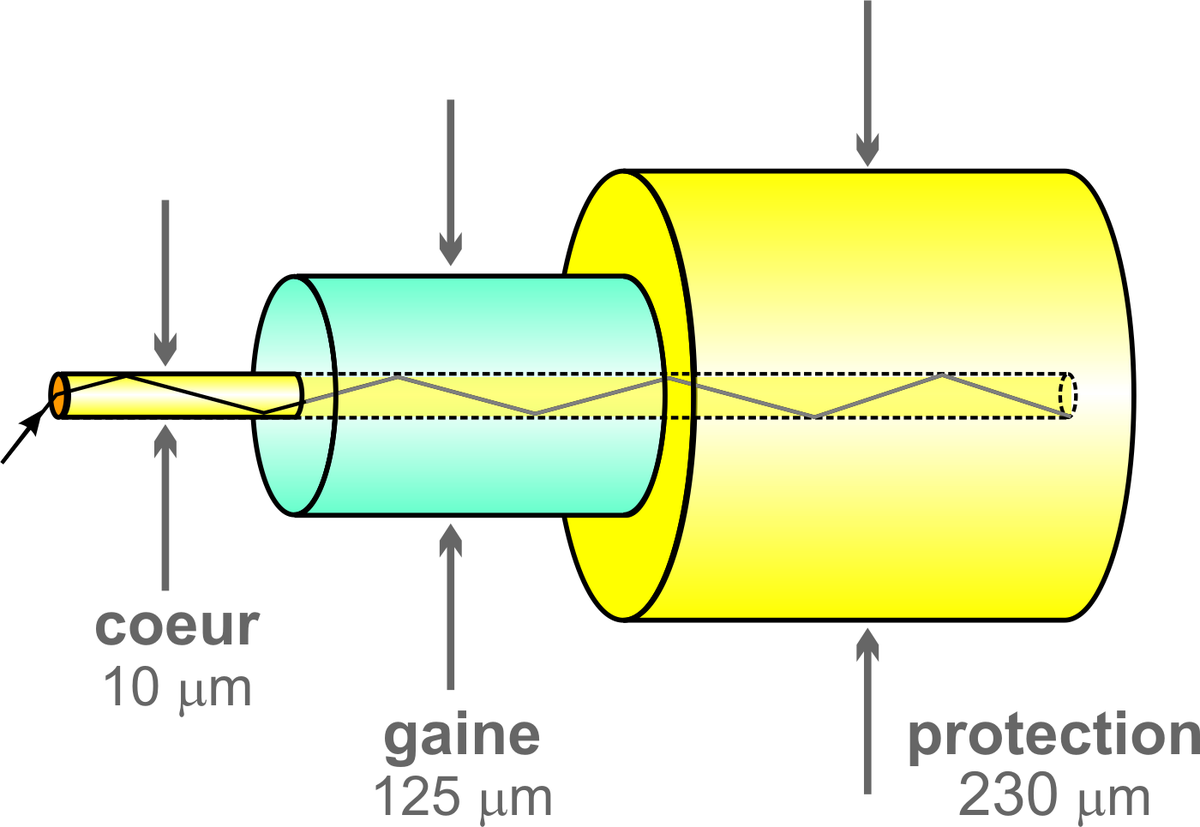
Cette dernière est représentée par un tube de verre ou de plastique, translucide, qui conduit un ou plusieurs faisceau de lumière comme le montre le schéma suivant :
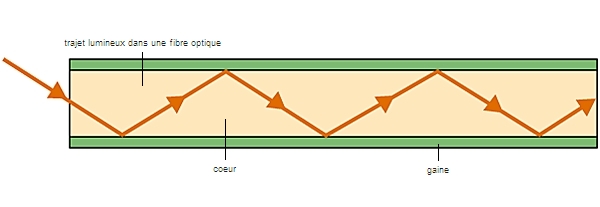
On remarque que le faisceau de lumière se dissipe pas dans la gaine et est entièrement réfléchi dans le coeur. Ce phénomène s'appelle la réflexion totale. Les scientifiques Snell et Descartes en ont établi une loi : \(\displaystyle \sin\left(angle\right)=\frac{\text{indice de la gaine}}{\text{indice du coeur}}\). Une loi ici qui n'est évidemment pas à apprendre dans cette séquence !
Nous remarquons cependant qu'une nouvelle opération apparait : le sinus d'un angle. C'est ce que nous allons voir dans cette séquence.
II) Rappels sur le triangle rectangle
Durant la séquence, nous nous baserons sur le triangle rectange suivant avec les notations précisées de la façon suivanes :
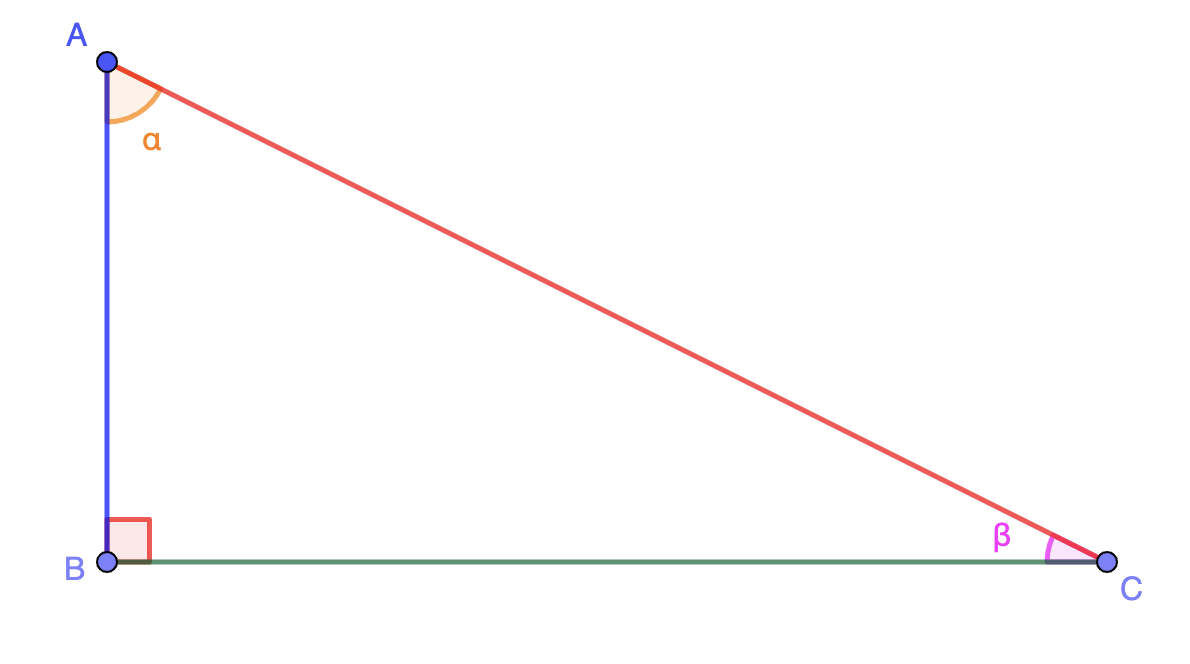
Le plus grand côté est appelé l'hypoténuse. Ici, c'est le segment \(\displaystyle \color{red}{\left[AC\right]}\).
L'angle droit est noté \(\displaystyle \color{red}{\widehat{CAB}}\).
L'angle \(\displaystyle \color{orange}{\widehat{BAC}}\) est noté \(\displaystyle \color{orange}{\alpha}\)
L'angle \(\displaystyle \color{magenta}{\widehat{ACB}}\) est noté \(\displaystyle \color{magenta}{\beta}\)
III) Rappels sur le cosinus
On rappelle la définition du cosinus de la façon suivante :
Définition : Dans le triangle rectangle, le cosinus d'un angle aigu est égal au rapport de la longueur du côté adjacent à cet angle aigu et la longueur de l'hypoténuse.
Dans le triangle rectangle \(\displaystyle ABC\) rectangle en \(\displaystyle B\), si on considère l'angle aigu \(\displaystyle \color{orange}{\alpha}\). Son cosinus s'écrit donc \( \displaystyle\cos\left(\color{orange}{\alpha}\right)=\frac{\color{blue}{AB}}{\color{red}{AC}}\).
Dans le triangle rectangle \(\displaystyle ABC\) rectangle en \(\displaystyle B\), si on considère l'angle aigu \(\displaystyle \color{magenta}{\beta}\). Son cosinus s'écrit donc \( \displaystyle\cos\left(\color{magenta}{\beta}\right)=\frac{\color{green}{BC}}{\color{red}{AC}}\).
Pour les exemples d'utilisation, se conférer aux rédactions types suivantes (vues en classe de quatrième) :
Comment calculer une longueur avec le cosinus ?
Comment calculer un angle avec le cosinus ?
IV) Le sinus d'un angle
Le sinus se définit de la façon suivante :
Définition : Dans le triangle rectangle, le sinus d'un angle aigu est égal au rapport de la longueur du côté oposé à cet angle aigu et la longueur de l'hypoténuse.
Dans le triangle rectangle \(\displaystyle ABC\) rectangle en \(\displaystyle B\), si on considère l'angle aigu \(\displaystyle \color{orange}{\alpha}\). Son sinus s'écrit donc \( \displaystyle\sin\left(\color{orange}{\alpha}\right)=\frac{\color{green}{BC}}{\color{red}{AC}}\).
Dans le triangle rectangle \(\displaystyle ABC\) rectangle en \(\displaystyle B\), si on considère l'angle aigu \(\displaystyle \color{magenta}{\beta}\). Son sinus s'écrit donc \( \displaystyle\sin\left(\color{magenta}{\beta}\right)=\frac{\color{blue}{AB}}{\color{red}{AC}}\).
Pour les exemples d'utilisation, se conférer aux rédactions types suivantes :
Comment calculer une longueur avec le sinus ?
Comment calculer un angle avec le sinus ?
V) La tangente d'un angle
La tangente se définit de la façon suivante :
Définition : Dans le triangle rectangle, la tangente d'un angle aigu est égal au rapport de la longueur du côté oposé à cet angle aigu et la longueur du côté adjacent de cet angle.
Dans le triangle rectangle \(\displaystyle ABC\) rectangle en \(\displaystyle B\), si on considère l'angle aigu \(\displaystyle \color{orange}{\alpha}\). Sa tangente s'écrit donc \( \displaystyle\tan\left(\color{orange}{\alpha}\right)=\frac{\color{green}{BC}}{\color{blue}{AB}}\).
Dans le triangle rectangle \(\displaystyle ABC\) rectangle en \(\displaystyle B\), si on considère l'angle aigu \(\displaystyle \color{magenta}{\beta}\). Sa tangente s'écrit donc \( \displaystyle\tan\left(\color{magenta}{\beta}\right)=\frac{\color{blue}{AB}}{\color{green}{BC}}\).
Pour les exemples d'utilisation, se conférer aux rédactions types suivantes :
Comment calculer une longueur avec la tangente ?
Comment calculer un angle avec la tangente ?
VI) Relations entre le cosinus, le sinus et la tangente.
Il existe deux relations en classe de troisième qui permettent de lier le cosinus, le sinus et la tangente :
Propriété : Dans un triangle rectangle, pour tout angle aigu de mesure \(\displaystyle x\), on a \(\displaystyle \cos^2\left(x\right)+\sin^2\left(x\right)=1\).
Propriété : Dans un triangle rectangle, pour tout angle aigu de mesure \(\displaystyle x\), on a \(\displaystyle \tan\left(x\right)=\frac{\sin\left(x\right)}{\cos\left(x\right)}\).