Enoncé de l'exercice n° 7-1 : (Extrait : n°108 page 238 livre 2nde Hachette Education)
La puissance \(\displaystyle P\) (en watt W) dissipée dans une résistance peut s'exprimer en fonction de la tension \(\displaystyle U\) (en volt V) du cournt continu aux bornes d'une résistance \(\displaystyle R\) (en ohm \(\displaystyle \Omega\)) par la formule \(\displaystyle P=\frac{U^2}{R}\).
Question 1 : Quelle est la puissance dissipée dans une résistance \(\displaystyle R\) de 10\(\displaystyle \Omega\) lorsque \(\displaystyle U=10\)V ?
Question 2 : Calculer la tension \(\displaystyle U\) pour \(\displaystyle R=6\Omega\) et \(\displaystyle P=5\)W.
Question 3 : Calculer la résistance \(\displaystyle R\) dans le cas où \(\displaystyle U=10\)V et \(\displaystyle P=8\)W.
Question 4 : On suppose que \(\displaystyle R=100\Omega\). Quelles puissances peut-on obtenir lorsque la tension est comprise entre 0 et 220 V ?
Question 5 : Soit \(\displaystyle R\) une résistance fixée, strictement positive. Que peut-on dire de la puissance lorsque la tension augmente ?
Question 4 : Dans ce cas, la puissance est-elle proportionnelle à la tension ?
Question 4 : On suppose ici que \(\displaystyle U\) est fixée. Que peut-on dire de la puissance lorsque la résistance augmente ?
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-2 : (Extrait : n°114 page 239 livre 2nde Hachette Education)
La planète Mercure est assimilée à une shpère de diamètre \(\displaystyle d\), compris enctre \(\displaystyle 4,8\times10^3\)km et \(\displaystyle 4,9\times10^3\)km.
Question 1 : Sachant que le volume \(\displaystyle V\) d'une boule en fonction de son rayon \(\displaystyle R\) est \(\displaystyle V=\frac{4}{3}\pi R^3\), exprimer \(\displaystyle V\) en fonction de \(\displaystyle d\).
Question 2 : Donner un encadrement de \(\displaystyle V\), en m3 à 109 près.
Question 3 : On rappelle que la masse volumique \(\displaystyle \rho\) d'un corps se calcule par l'expression \(\displaystyle \rho=\frac{M}{V}\), où \(\displaystyle M\) désigne la masse d'un corps occupant un volume \(\displaystyle V\). L'étude télescopique de la planète Mercure laisse supposer que la masse de cette planète est comprise entre \(\displaystyle 3,2\times10^{23}\)kg et \(\displaystyle 3,3\times10^{23}\)kg. Donner un encadrement de la masse volumique de la planète Mercure, en kg/m3 puis en g/cm3 (à 0,01 près).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-3 : (Extrait : n°79 page 293 livre 2nde Hachette Education)
Sur une route sèche et horizontale, la distance de freinage \(\displaystyle D\), en mètre, d'une voiture à partir de l'instant où le conducteur appuie sur le frein est donnée par la formule \(\displaystyle D=\frac{v^2}{2gc}\) où \(\displaystyle v\) est la vitesse à l'instant du freinag, en m/s ; \(\displaystyle g\) l'intensité de la pensanteur qui vaut 9,81 m/s2 à Paris et \(\displaystyle c\), le coefficient de frottement longitudinal dépendant de la nature et de la qualité du révêtement qui vaut ici 0,7.
Question 1 : Justifier que lorsque la vitesse à l'instant du freinage est de 50 km/h, la distance de freinage vaut environ 14m.
Question 2 : Quelle est la distance de freinage lorsque la vitesse à l'instant du freinage est de 110 km/h ?
Question 3 : Etudier les variations de la fonction définie sur \(\displaystyle \left[0;+\infty\right[\) par \(\displaystyle f:v\longmapsto D\). Interpréter pour la siuation étudiée.
Question 4 : La distance de freinage \(\displaystyle D\) est-elle proportionnelle à la vitesse \(\displaystyle v\) ?
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-4 : (Extrait : n°83 page 293 livre 2nde Hachette Education)
En assimilant la trajectoire d'un satellite tournant autour de la Terre à un cercle, on peut montrer que sa vitesse \(\displaystyle v\) de rotation (en m/s) vérifie \(\displaystyle v=\sqrt{\frac{GM}{r}}\) où \(\displaystyle r\) est la distance (en m) entre le satelitte et le centre de la Terre, \(\displaystyle M\) est la masse de la Terre (en kg) et \(\displaystyle G\) est la constante de gravitation universelle.
Question 1 : Que peut-on dire de la vitesse \(\displaystyle v\) de rotation lorsque la distance \(\displaystyle r\) augmente ? Que peut-on en déduire pour la fonction \(\displaystyle f:r\longmapsto v\) ?
Question 2 : On donne \(\displaystyle G=6,67\times10^{-11}\) et \(\displaystyle M=5,97\times10^{24}\). Sachant que le rayon de la Terre est \(\displaystyle R=6370\)km, déterminer l'altitude d'un satellite géostationnaire, c'est-à-dire d'un satellite ayant la même vitesse de rotation que la Terre.
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-5 : (Extrait : n°86 page 294 livre 2nde Hachette Education)
Un T.P. de chimie consiste à mettre en relation le volume de la pressiond 'un gaz, à température ambiante. Voici les résultats obtenus :
| \(\displaystyle V\) (en mL) | 50 | 46 | 42 | 34 | 30 | 26 | 22 |
| \(\displaystyle P\) (en kPa) | 58 | 63 | 68 | 83 | 95 | 108 | 127 |
Question 1 : Construire le nuage de points associé au tableau précédent.
Question 2 : On cherche à déterminer une fonction qui au volume du gaz associe la pression. Laquelle de ces trois propositions semble la plus adaptée : \(\displaystyle f\left(x\right)=-2x+151\) ; \(\displaystyle g\left(x\right)=-1,25x+120\) ; \(\displaystyle h\left(x\right)=\frac{2840}{x}\) ?
Question 3 : Utiliser la réponse précédente pour déterminer le volume occupé par le gaz lorsque la pression vaut 150000 Pa.
Question 4 : Utiliser la réponse de la question 2 pour déterminer la pression du gaz lorsque son volume vaut 0,5 L.
Question 5 : Recopier et compléter les pointillés, en argumentant : « Lorsque le volume d'un gaz augmente, alors sa pression ... »
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-6 : (Extrait : n°90 page 295 livre 2nde Hachette Education)
On considère la fonction \(\displaystyle f\) définie sur \(\displaystyle \mathbb{R}\) par \(\displaystyle f\left(x\right)=-2\left(x-3\right)^2+5\).
On considère ensuite le programme de calcul suivant :
Saisir \(\displaystyle x\)
Soustraire 3
Elevé au carré
Multiplier par -2
Ajouter 5
Afficher le résultat
Question 1 : Grâce à la calculatrice, conjecturer le tableau de variations de \(\displaystyle f\).
Question 2 : Quel est le rôle du programme de calcul ?
Question 3 : On rappelle la propriété suivante : Pour tout \(\displaystyle A\) et \(\displaystyle B\), si \(\displaystyle A < B < 0\) alors \(\displaystyle A^2 > B^2\). En s'inspirant du programme de calcul précédent, en déduire une démonstration du sens de variations de \(\displaystyle f\) sur l'intervalle \(\displaystyle \left]-\infty;3\right]\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-7 : (Extrait : n°91 page 295 livre 2nde Hachette Education)
L'épaisseur \(\displaystyle d\) d'un cheveu peut être déterminée pr diffraction. Pour cela, on l'éclaire avec un lazer (de longueur d'onde \(\displaystyle \lambda\)).
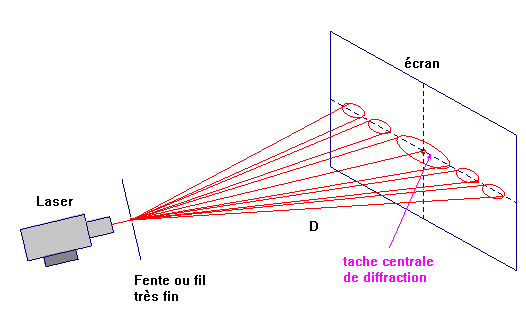
La lumière est alors diffractée par le cheveu et on observe plusieurs tâches lumineuses sur un écran placé à une distance \(\displaystyle D\) du cheveu, réparties systématiquement autour d'une tâche lumineuse centrale, plus grande, de largeur \(\displaystyle L\).

La théorie physique montre que \(\displaystyle d=\frac{2\lambda D}{L}\).
Les longueurs \(\displaystyle d\), \(\displaystyle D\) et \(\displaystyle L\) sont en mètre et la longueur d'onde \(\displaystyle \lambda\) est en micromètre.
Question 1 : On fixe les valeurs de \(\displaystyle \lambda\) et de \(\displaystyle D\). Quel est le sens de variation de la fonction \(\displaystyle f : L\longmapsto d\) ?
Question 2 : Interpréter dans le contexte de l'exercice.
Question 3 : En pratique, on sait que le laser dispose de l'information technique suivante : « \(\displaystyle \lambda \simeq 635 - 770\)nm ». On sait que \(\displaystyle D\) est mesurée avec un mètre ruban à 5 mm près et enfin on sait que \(\displaystyle L\) est mesurée avec un double décimètre à 1 mm près. On a mesuré \(\displaystyle D=4\)m et \(\displaystyle L=8\)mm. Estimer l'épaisseur \(\displaystyle d\) du cheveu, en indiquant avec précision celle-ci est donnée.
Envoyer la proposition de travail
Lancer l'interactivité
On considère une fonction \(\displaystyle f\) définie sur l'intervalle \(\displaystyle I=\left[-15;12\right]\) par \(\displaystyle f\left(x\right)=\frac{3-7x}{4}\).
Question 1 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left[-15;12\right]\).
Question 2 : Dresser le tableau de variations de \(\displaystyle f\) sur \(\displaystyle \left[-15;12\right]\).
Envoyer la proposition de travail
Lancer l'interactivité
On considère une fonction \(\displaystyle f\) définie sur l'intervalle \(\displaystyle I=\left[-5;5\right]\) par \(\displaystyle f\left(x\right)=\frac{1}{2}\left(x-2\right)^2-2\).
Question 1 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left[-5;2\right]\).
Question 2 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left[2;5\right]\).
Question 3 : Dresser le tableau de variations de \(\displaystyle f\) sur \(\displaystyle \left[-5;5\right]\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-10 :
On considère une fonction \(\displaystyle f\) définie sur l'intervalle \(\displaystyle I=\left[-5;+\infty\right[\) par \(\displaystyle f\left(x\right)=7\left(3x-2\right)^2\).
Question 1 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left[-5;\frac{2}{3}\right]\).
Question 2 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left[\frac{2}{3};+\infty\right[\).
Question 3 : Dresser le tableau de variations de \(\displaystyle f\) sur \(\displaystyle \left[-5;+\infty\right[\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-11 :
On considère une fonction \(\displaystyle f\) définie sur l'intervalle \(\displaystyle I=\left]-\infty;3\right[\cup\left]3;+\infty\right[\) par \(\displaystyle f\left(x\right)=\frac{2}{x-3}+1\).
Question 1 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left]-\infty;3\right[\).
Question 2 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left]3;+\infty\right[\).
Question 3 : Dresser le tableau de variations de \(\displaystyle f\) sur \(\displaystyle \left]-\infty;3\right[\cup\left]3;+\infty\right[\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-12 :
On considère une fonction \(\displaystyle f\) définie sur l'intervalle \(\displaystyle I=\left[-1;+\infty\right[\) par \(\displaystyle f\left(x\right)=-2\sqrt{x+1}\).
Question 1 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left[-1;+\infty\right[\).
Question 2 : Dresser le tableau de variations de \(\displaystyle f\) sur \(\displaystyle \left[-1;+\infty\right[\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-13 :
On considère une fonction \(\displaystyle f\) définie sur l'intervalle \(\displaystyle I=\left]-\infty;2\right[\cup\left]2;+\infty\right[\) par \(\displaystyle f\left(x\right)=\frac{1}{2-x}\).
Question 1 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left]-\infty;2\right[\).
Question 2 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left]2;+\infty\right[\).
Question 3 : Dresser le tableau de variations de \(\displaystyle f\) sur \(\displaystyle \left]-\infty;2\right[\cup\left]2;+\infty\right[\).
Envoyer la proposition de travail
Lancer l'interactivité
Enoncé de l'exercice n° 7-14 :
On considère une fonction \(\displaystyle f\) définie sur l'intervalle \(\displaystyle I=\left[-7;9\right]\) par \(\displaystyle f\left(x\right)=-\frac{\left(1-x\right)^2}{3}-\frac{3}{2}\).
Question 1 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left[-7;1\right]\).
Question 2 : Etudier les variations de \(\displaystyle f\) sur \(\displaystyle \left[1;9\right]\).
Question 3 : Dresser le tableau de variations de \(\displaystyle f\) sur \(\displaystyle \left[-7;9\right]\).
Envoyer la proposition de travail
Lancer l'interactivité