I) Mise en situation
Dans la vie professionnelle, et en particulier dans des situations rencontrées en physique, des phénomènes ou des concepts sont modélisés par des fonctions.
A titre d'exemple, on se propose de regarder l'activité n°9 dont le fichier est disponible en cliquant ici. On considère le lancement d'un projectile avec une vitesse initiale \(\displaystyle V_0\) et faisant un angle \(\displaystyle \alpha\) avec le plan horizontal, et se trouvant à une altitude \(\displaystyle h\). La fonction \(\displaystyle f\) qui permet de donner les coordonnées cartésiennes \(\displaystyle M\left(x;y\right)\) des points \(\displaystyle M\) de la trajectoire de ce projectile dans l'atmosphère terrestre s'écrit \(\displaystyle f\left(x\right)=\frac{-gx^2}{2V_0^2\cos^2\left(\alpha\right)}+\tan\left(\alpha\right)x+h\) en considérant ici que les ordonnées \(\displaystyle y\) sont données par la fonction \(\displaystyle f\).
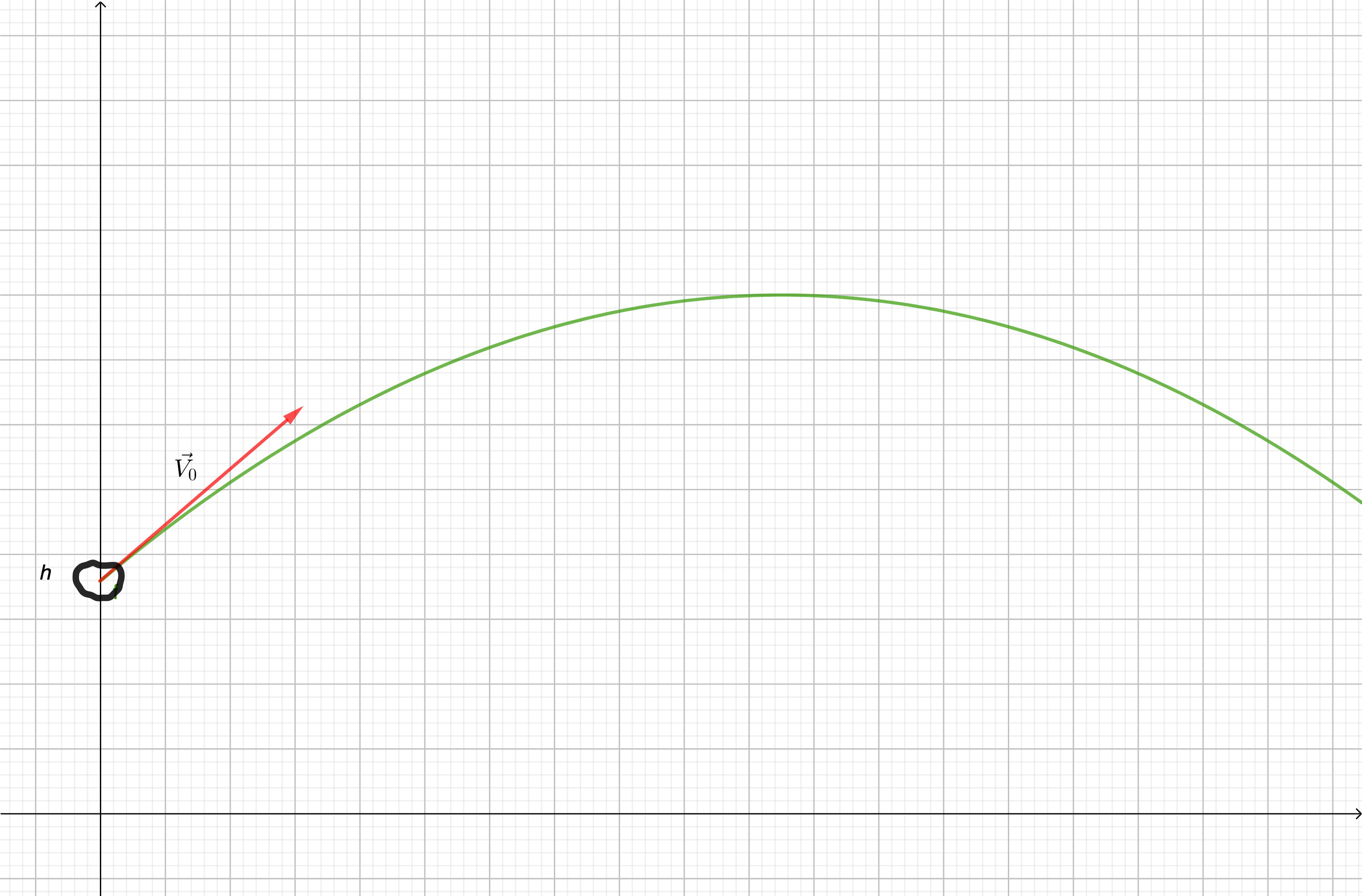
En modifiant quelques paramètres, on peut lancer un deuxième projectile. Une deuxième fonction, notée \(\displaystyle g\) nous permetrait d'avoir une équation similaire du type \(\displaystyle g\left(x\right)=\frac{-gx^2}{2V_0'^2\cos^2\left(\alpha'\right)}+\tan\left(\alpha'\right)x+h'\).
A partir de ces deux lancés, on pourrait déterminer différents résultats comme par exemple sur quelle distance le premier projectile est-il plus haut que le deuxième.
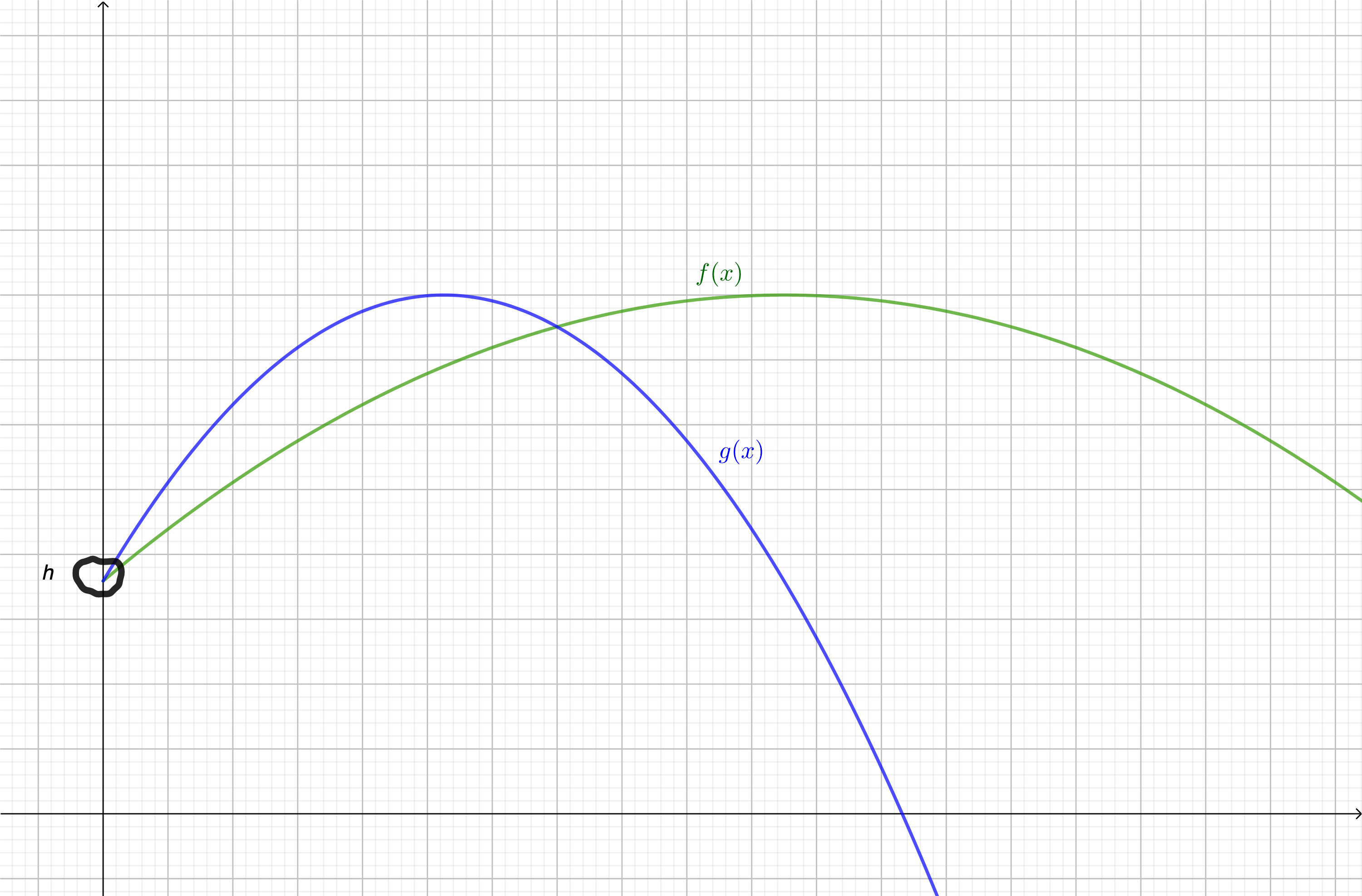
Cette résolution de problème se traduit mathématiquement par l'inéquation \(\displaystyle f\left(x\right) > g\left(x\right)\), ce qui revient à résoudre l'inéquation \(\displaystyle \frac{-gx^2}{2V_0^2\cos^2\left(\alpha\right)}+\tan\left(\alpha\right)x+h-\frac{-gx^2}{2V_0'^2\cos^2\left(\alpha'\right)}-\tan\left(\alpha'\right)x-h' > 0\)
Une telle inéquation ne se résout plus aussi simplement que celles vues en classe de troisième. De nouvelles méthodes s'imposent et font l'objet de cette séquence.
II) Signe d'une fonction
Avant d'entrer dans les méthodes de résolution, il est important de maîtriser la notion du signe d'une fonction.
1) Le tableau de signes
Le concept du tableau de signes utilise les définitions suivantes :
Définition : On dit qu'une fonction \(\displaystyle f\) est positive sur un intervalle \(\displaystyle I\) si, pour toute valeur \(\displaystyle x\) de \(\displaystyle I\), on a \(\displaystyle f\left(x\right) \geqslant 0\).
Définition : On dit qu'une fonction \(\displaystyle f\) est négative sur un intervalle \(\displaystyle I\) si, pour toute valeur \(\displaystyle x\) de \(\displaystyle I\), on a \(\displaystyle f\left(x\right) \leqslant 0\).
Etudier le signe d'une fonction consiste ainsi à déterminer les ensembles sur lesquels elle est positive et ceux sur lesquels elle est négative. Les résultats sont souvent résumés dans un tableau de signes, qui n'est pas à confondre avec le tableau de variations.
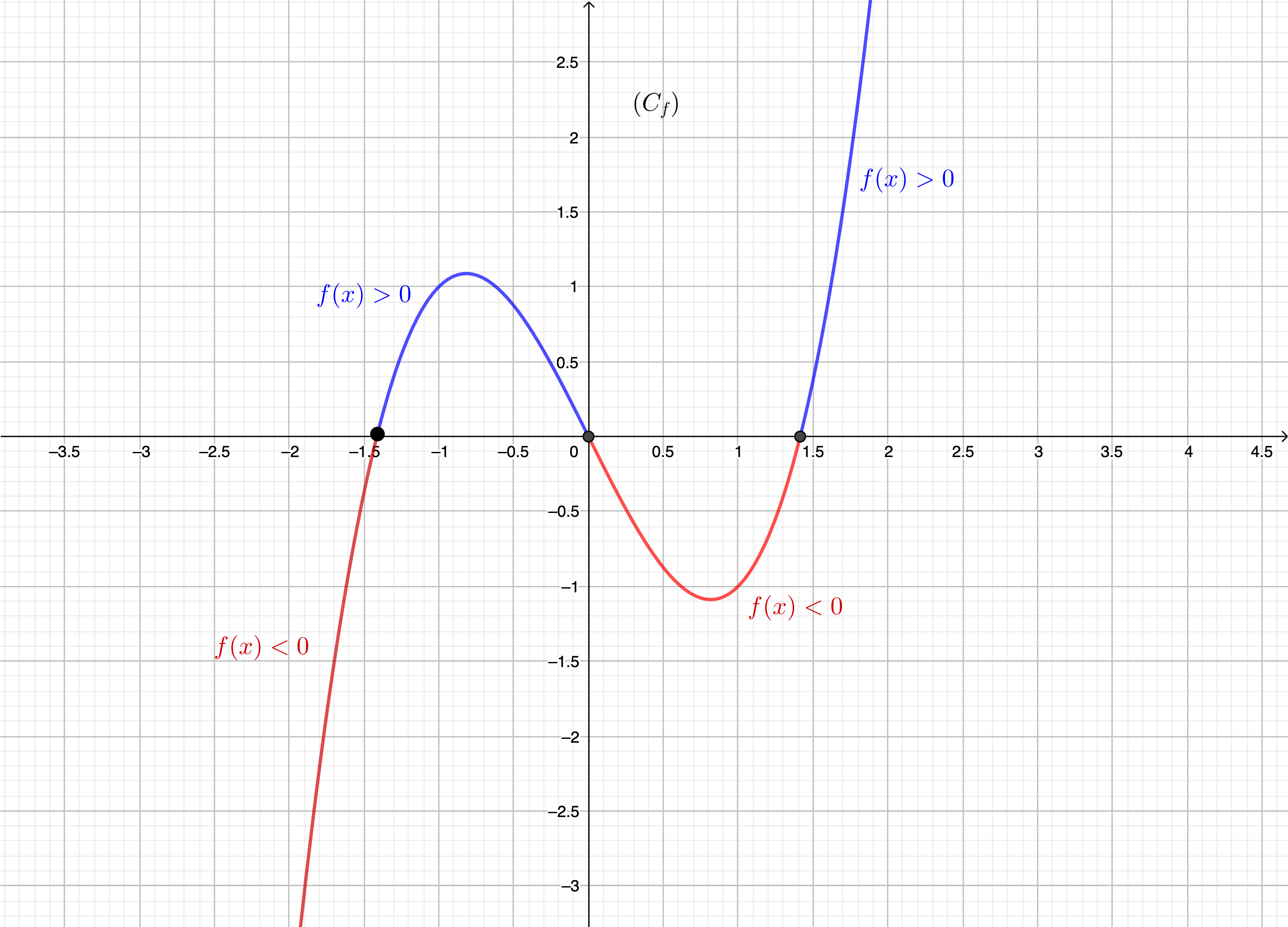
Le tableau de signe associé à cette fonction devient donc :

2) Cas particulier de la fonction affine
On rappelle qu'une fonction affine s'exprime par \(\displaystyle f\left(x\right)=mx+p\) avec \(\displaystyle m\) le coefficient directeur et \(\displaystyle p\), l'ordonnée à l'origine.
Propriété : Le signe d'une fonction affine dépend du signe du coefficient directeur \(\displaystyle m\) et change en \(\displaystyle \frac{-p}{m}\), unique solution de l'équation \(\displaystyle mx+p=0\).
On a ainsi deux cas de figures, selon la variation de la fonction affine :
• Cas où la fonction affine est croissante (\(\displaystyle m>0\)) : :
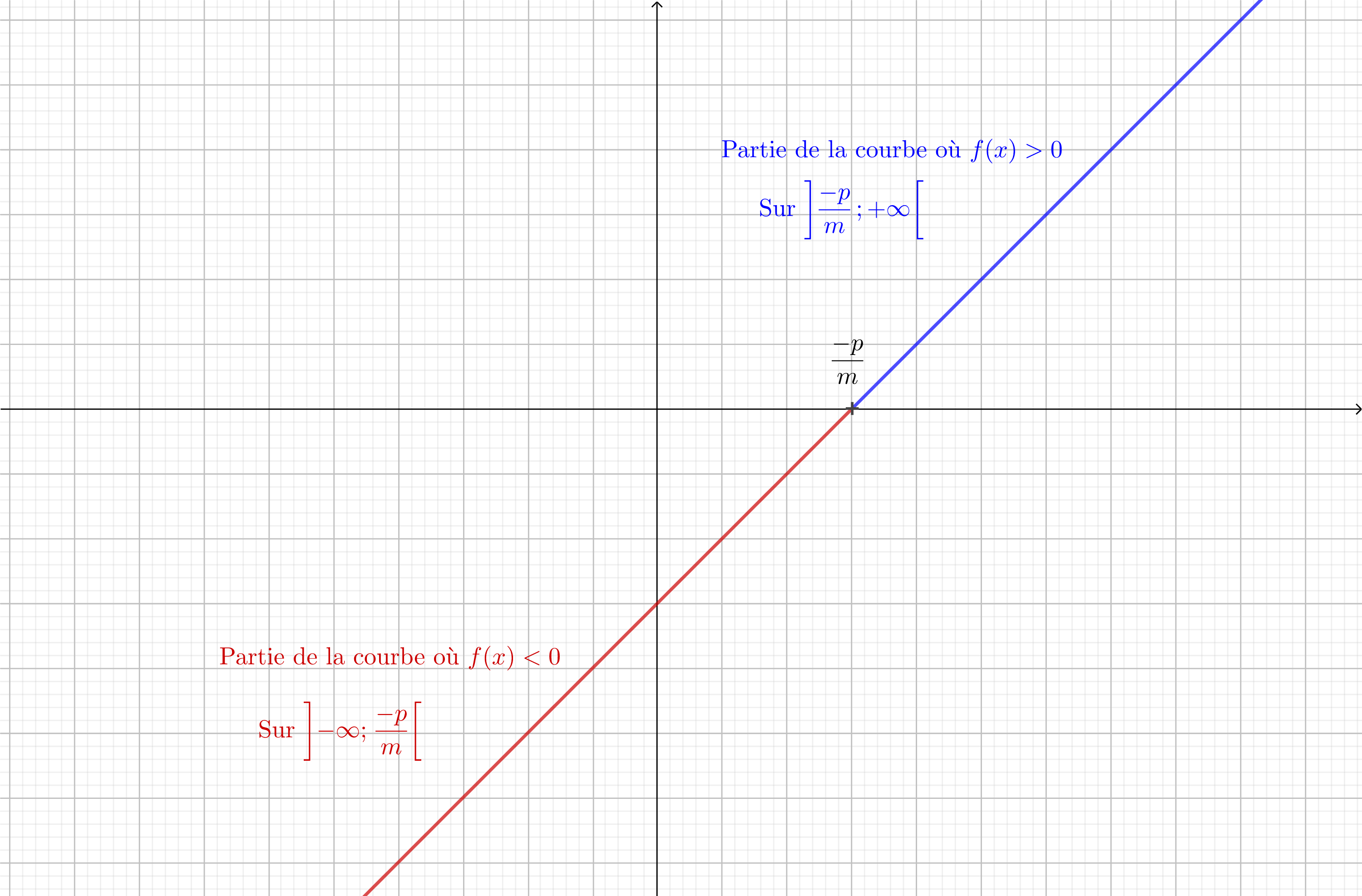

Démonstration : \(\displaystyle \begin{align*} f\left(x\right) &> 0 \\ mx+p &> 0 \\ mx &> -p \\ x &> \frac{-p}{m} \text{ avec ici } m > 0\\ \end{align*} \)
• Cas où la fonction affine est décroissante (\(\displaystyle m < 0\)) : :
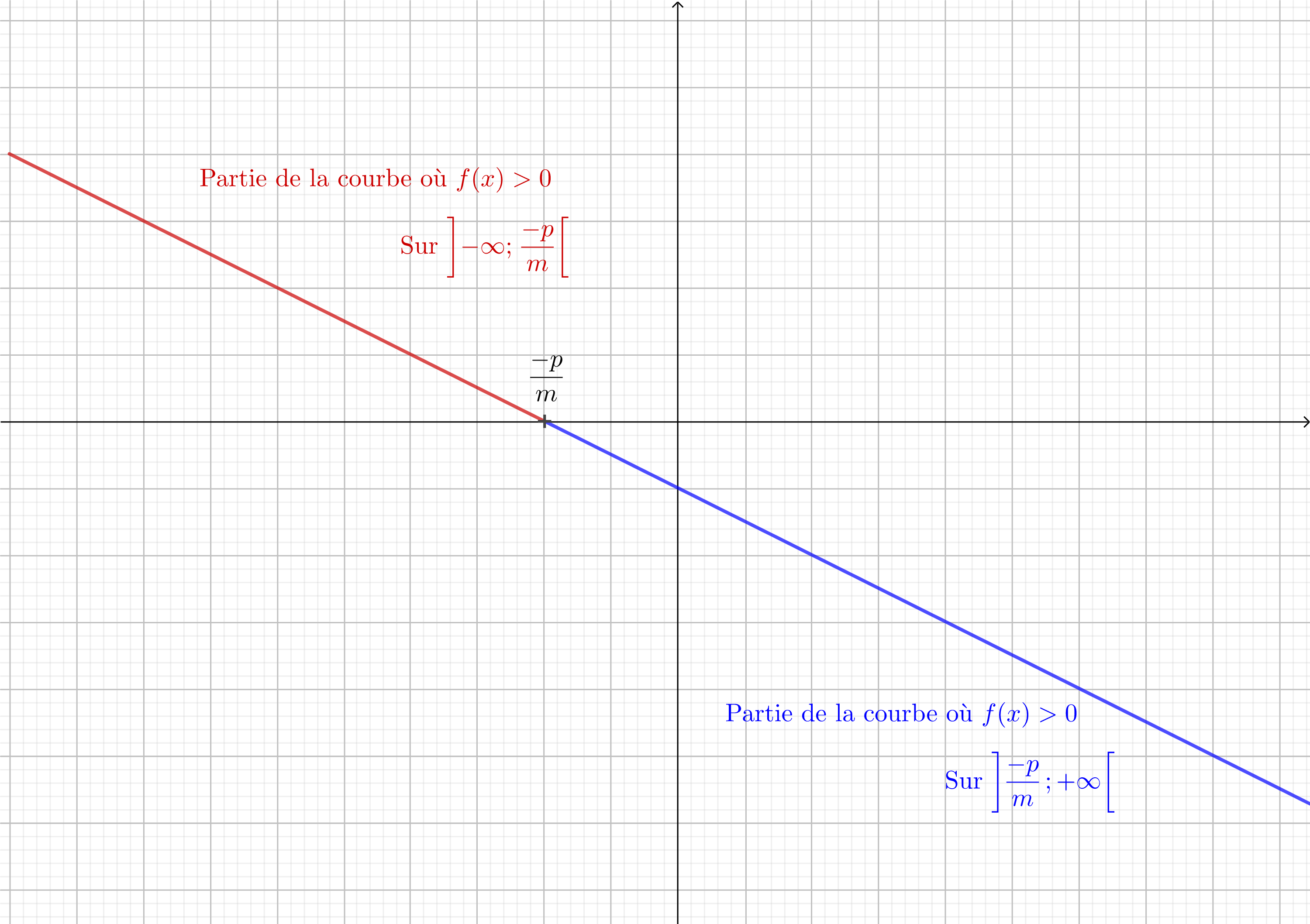

Démonstration : \(\displaystyle \begin{align*} f\left(x\right) &> 0 \\ mx+p &> 0 \\ mx &> -p \\ x &< \frac{-p}{m} \text{ avec ici } m < 0\\ \end{align*} \)
3) Deux exemples
On considère deux fonctions \(\displaystyle f\) et \(\displaystyle g\) définie sur \(\displaystyle \mathbb{R}\) par \(\displaystyle f\left(x\right)=\frac{-1}{2}x-2\) et \(\displaystyle g\left(x\right)=2x-6\). Leur courbe représentative respectives \(\displaystyle \left(C_f\right)\) et \(\displaystyle \left(C_g\right)\) donnent :
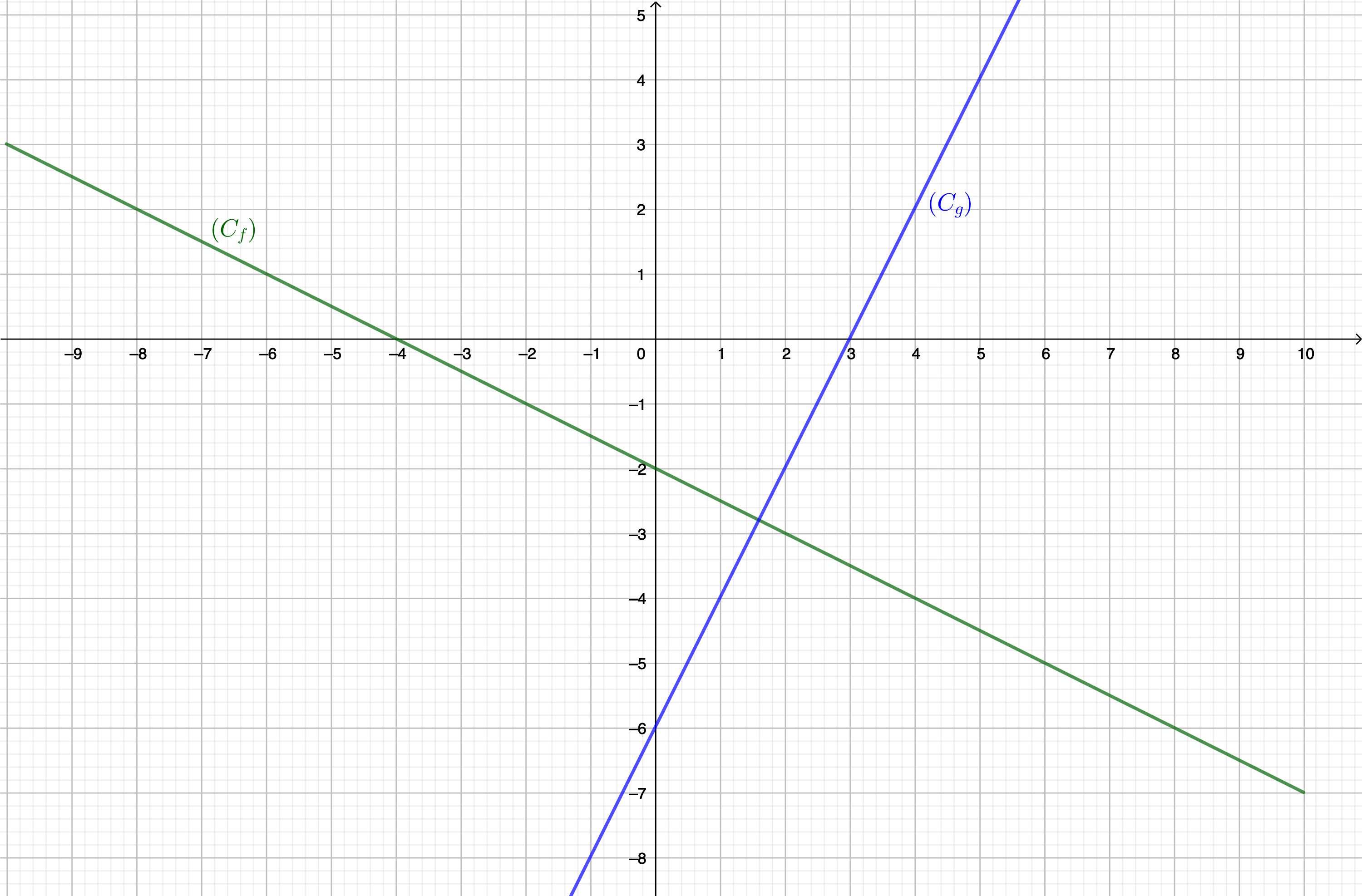
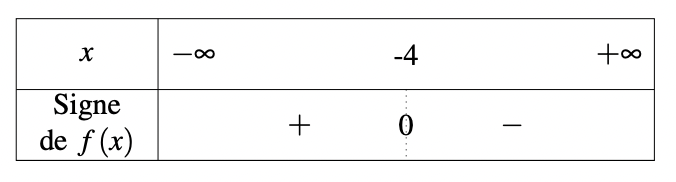
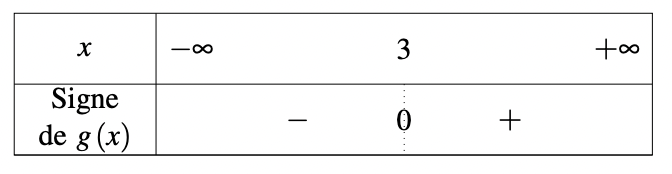
Pour la fonction \(\displaystyle f\), on a \(\displaystyle \frac{-p}{m}=-4\) et pour la fonction \(\displaystyle g\), \(\displaystyle \frac{-p}{m}=3\). Pour chaque fonction, ces valeurs sont appelées les valeurs charnières. Les tableaux de signe deviennent donc :
III Résolution d'équations et d'inéquations par méthode graphique
Dans ces méthodes, on considère deux fonctions \(\displaystyle f\) et \(\displaystyle g\) définies sur un même ensemble de définition noté \(\displaystyle D\). On note \(\displaystyle \left(C_f\right)\) et \(\displaystyle \left(C_g\right)\) leur courbe représentative dans un repère.
1) Résolution graphique d'équations
L'équation étudiée est du type \(\displaystyle f\left(x\right)=k\) ou \(\displaystyle f\left(x\right)=g\left(x\right)\).
Résoudre l'équation \(\displaystyle f\left(x\right)=k\) consiste à déterminer toutes les abscisses \(\displaystyle x\) des points de la courbe \(\displaystyle \left(C_f\right)\) dont les ordonnées \(\displaystyle y\) sont égales à \(\displaystyle k\).
Résoudre l'équation \(\displaystyle f\left(x\right)=g\left(x\right)\) consiste à déterminer toutes les abscisses \(\displaystyle x\) des points des courbes \(\displaystyle \left(C_f\right)\) et \(\displaystyle \left(C_g\right)\) dont les ordonnées \(\displaystyle y\) sont identiques.
Exemple 1 :
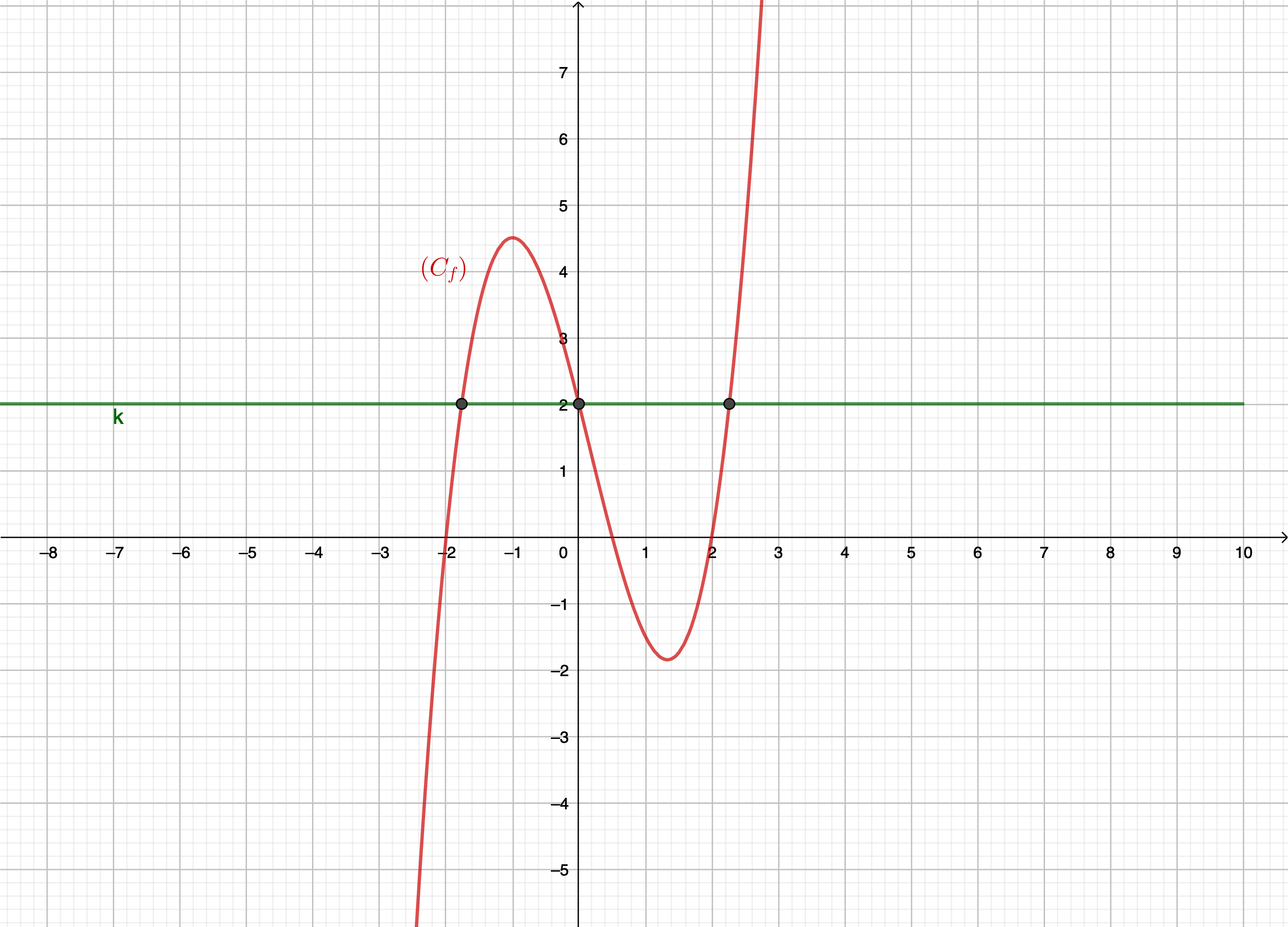
Graphiquement et avec la précision permise, on obtient \(\displaystyle x=-1,8\) ; \(\displaystyle x=0\) et \(\displaystyle x=2,2\).
Exemple 2 :
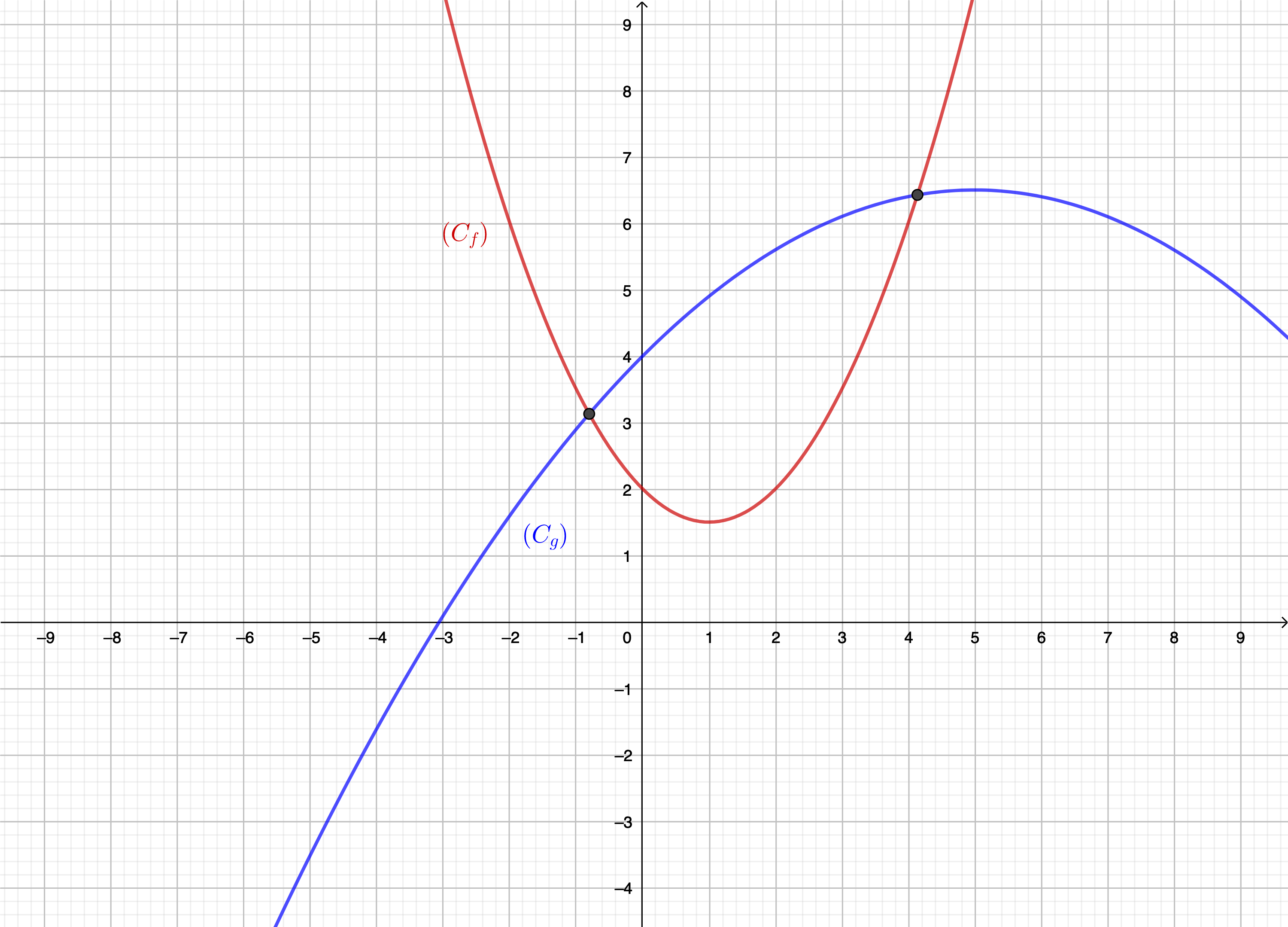
Graphiquement et avec la précision permise, on obtient \(\displaystyle x=-0,8\) et \(\displaystyle x=4,1\).
2) Résolution graphique d'inéquations
L'inéquation étudiée est du type \(\displaystyle f\left(x\right)>k\) ou \(\displaystyle f\left(x\right)\leqslant g\left(x\right)\).
Résoudre l'inéquation \(\displaystyle f\left(x\right) > k\) consiste à déterminer toutes les abscisses \(\displaystyle x\) des points de la courbe \(\displaystyle \left(C_f\right)\) dont les ordonnées \(\displaystyle y\) sont supérieures à \(\displaystyle k\).
Résoudre l'inéquation \(\displaystyle f\left(x\right) \leqslant g\left(x\right)\) consiste à déterminer toutes les abscisses \(\displaystyle x\) des points des courbes \(\displaystyle \left(C_f\right)\) et \(\displaystyle \left(C_g\right)\) dont les ordonnées \(\displaystyle y\) des points de \(\displaystyle \left(C_f\right)\) sont supérieurs à celles des points de \(\displaystyle \left(C_g\right)\).
Exemple 1 :
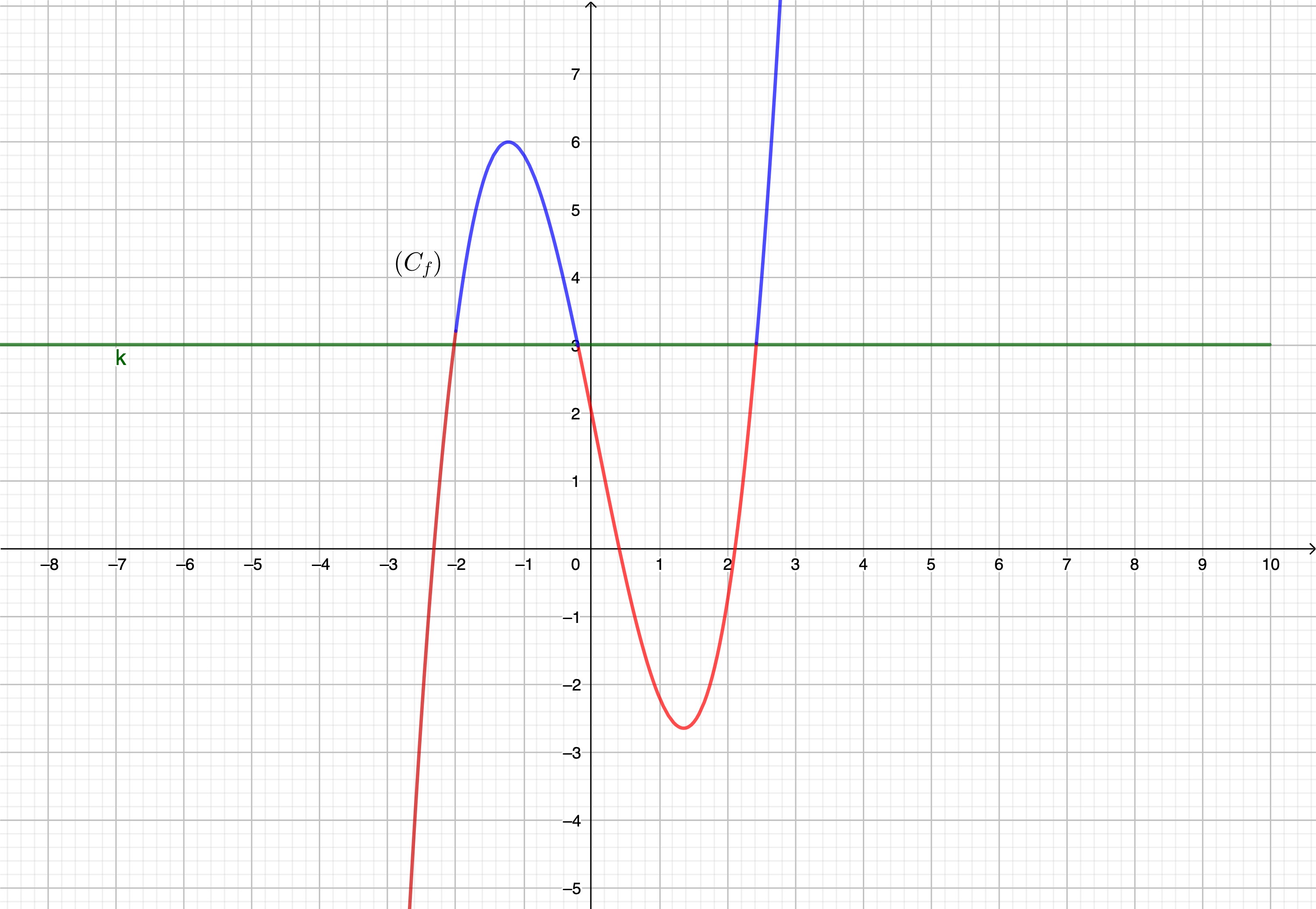
Graphiquement et avec la précision permise, on obtient \(\displaystyle x\in\left]-\infty;-2\right[\cup\left]-0,1;\frac{5}{2}\right[\) .
Exemple 2 :
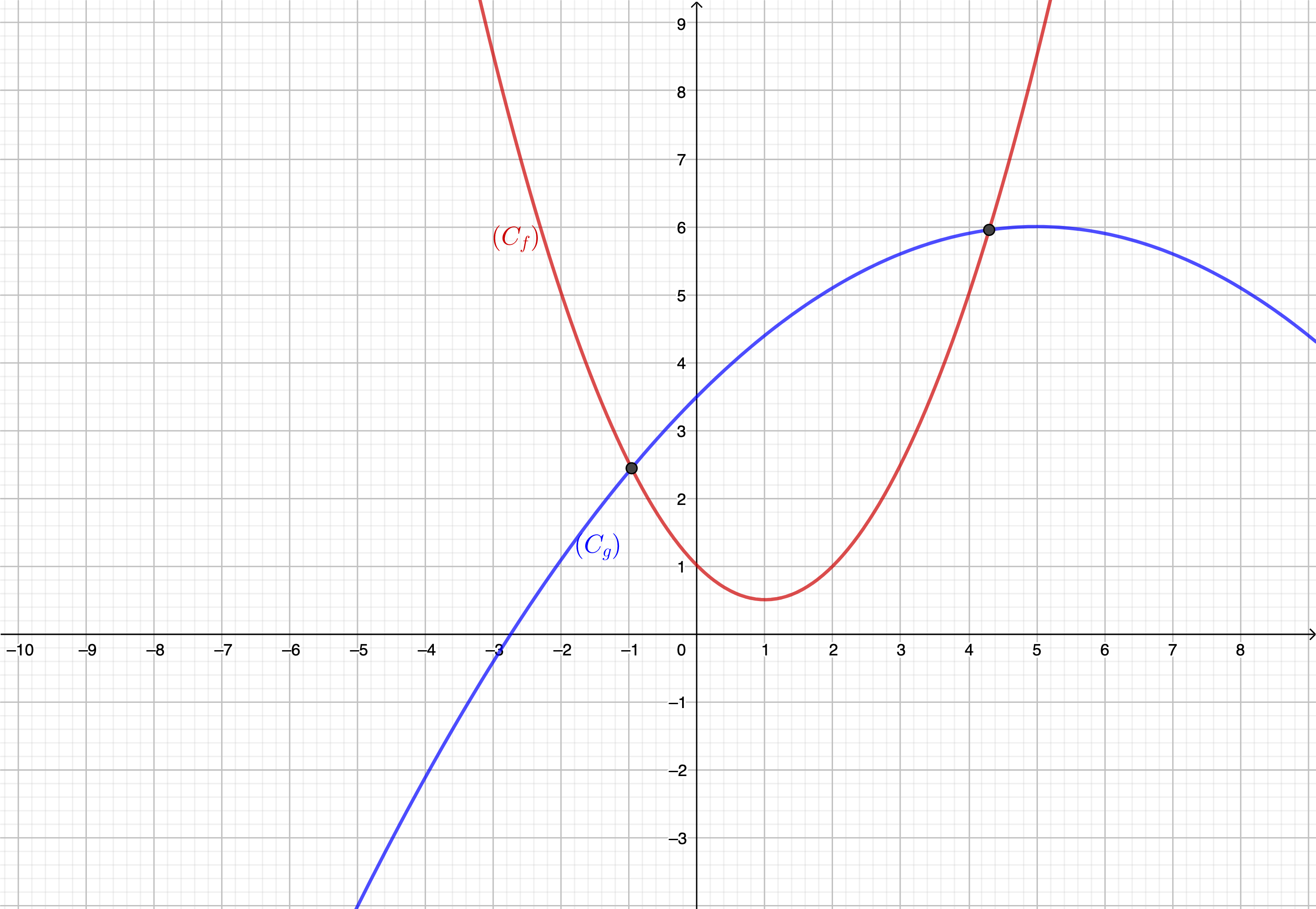
Graphiquement et avec la précision permise, on obtient \(\displaystyle x\in\left[-1;4,2\right]\).
IV) Résolution d'équations et d'inéquations par méthode algébrique
La résolution d'équations et d'inéquations par méthode algébrique repose sur les connaissances vues en classe de 3ème.
1) Rappels sur les équations du 1er degré
Pour résoudre une équation, il est nécessaire de connaitre la propriété suivante :
Propriété : Lorsqu'on développe, réduit, factorise chacun des membres d'une équation, les solutions ne changent pas.
Exemple : L'équation \(\displaystyle 7x-5=4\left(1-5x\right)\) est la même équation et donne les mêmes solutions que \(\displaystyle 7x-5=4-20x\).
Propriété : Lorsqu'on additionne ou on soustrait chacun des membres d'une équation par un même nombre, les solutions ne changent pas.
Exemple : L'équation \(\displaystyle 7x-5=4-20x\) est la même équation et donne les mêmes solutions que \(\displaystyle 7x-5+20x=4-20x+20x\).
Propriété : Lorsqu'on multiplie ou on divise chacun des membres d'une équation par un même nombre, les solutions ne changent pas.
Exemple : L'équation \(\displaystyle 27x=9\) est la même équation et donne les mêmes solutions que \(\displaystyle \frac{27x}{27}=\frac{9}{27}\).
2) Rappels sur les équations du type « produit nul »
Certaines équations peuvent s'écrire sous forme d'un produit du type « \(\displaystyle A\times B\) ». Il est dit nul lorsqu'on a \(\displaystyle A\times B=0\). On résoudre une telle équation, on utilise la propriété suivante :
Propriété : Un produit de facteurs est nul si au moins l'un des deux est nul.
Exemple : L'équation \(\displaystyle \left(3x-1\right)\left(2x+4\right)=0\) se résout de la façon suivante :
On cite la propriété : « Un produit de facteurs est nul si au moins l'un des deux est nul » :
\(\displaystyle \begin{align*} \text{D'une part } 3x-1&=0 & \text{ et d'autre part } 2x+4&=0 \\ 3x&=1 & 2x&=-4 \\ x&=\frac{1}{3} & x&=\frac{-4}{2} \\ & & x&=-2 \\ \end{align*} \)
Les solutions de l'équation sont \(\displaystyle x=\frac{1}{3}\) ou \(\displaystyle x=-2\). Ces solutions peuvent être notées aussi avec l'ensemble \(\displaystyle S=\left\{-2;\frac{1}{3}\right\}\).
3) Rappels sur les inéquations du 1er degré
Pour résoudre une inéquation, on utilise la définition et la propriété suivante :
Définition : Une inéquation est une inégalité dans laquelle figurent les nombres inconnus désignés par des lettres. Les solutions d'une inéquation sont les valeurs que l'on peut attribuer aux lettres pour que l'inégalité soit vraie. Résoudre une inéquation revient à trouver toutes les solutions.
Propriété : Lorsqu'on développe, réduit, factorise chacun des membres d'une inéquation, les solutions ne changent pas.
Exemple : L'équation \(\displaystyle 8\left(x+2\right)\geqslant9+10x\) est la même inéquation et donne les mêmes solutions que \(\displaystyle 8x+16\geqslant9+10x\).
Propriété : Lorsqu'on additionne ou on soustrait chacun des membres d'une inéquation par un même nombre, les solutions ne changent pas.
Exemple : L'équation \(\displaystyle 8x+16-10x\geqslant9+10x-10x\) est la même inéquation et donne les mêmes solutions que \(\displaystyle -2x+16\geqslant9\).
Propriété : Lorsqu'on multiplie ou on divise chacun des membres d'une équation par un même nombre positif non nul, les solutions ne changent pas.
Exemple : L'équation \(\displaystyle -2x\geqslant-7\) est la même équation et donne les mêmes solutions que \(\displaystyle -2x\times\frac{1}{2}\geqslant-7\times\frac{1}{2}\).
Propriété : Lorsqu'on multiplie ou on divise chacun des membres d'une équation par un même nombre négatif non nul, les solutions ne changent pas mais le signe de l'inéquation change.
Exemple : L'équation \(\displaystyle -2x\geqslant-7\) est la même équation et donne les mêmes solutions que \(\displaystyle -2x\times\frac{1}{-2}\leqslant-7\times\frac{1}{-2}\).
4) Les inéquations du type « produit nul »
Pour résoudre une telle inéquation, on déterminer le signe de chaque facteur puis on applique la règle des signes sur le produit. L'idéal est de réaliser l'étude à l'aide d'un tableau de signes :
Exemple : Considérons l'inéquation \(\displaystyle \left(x-5\right)\left(-2x+3\right) > 0\). L'étude se réalise de la façon suivante :
• le premier facteur \(\displaystyle x-5\) est une fonction affine qui s'annule en \(\displaystyle x=5\). Elle est croissante car \(\displaystyle m > 0\). Elle sera négative sur \(\displaystyle \left]-\infty;5\right]\) et positive sur \(\displaystyle \left[5;+\infty\right[\).
• le deuxième facteur \(\displaystyle -2x+3\) est une fonction affine qui s'annule en \(\displaystyle x=\frac{3}{2}\). Elle est décroissante car \(\displaystyle m < 0\). Elle sera positive sur \(\displaystyle \left]-\infty;\frac{3}{2}\right]\) et négative sur \(\displaystyle \left[\frac{3}{2};+\infty\right[\).
• les valeurs \(\displaystyle x=\frac{3}{2}\) et \(\displaystyle x=5\) sont appelées les valeurs charnières.
• On résulme l'étude avec l'application de la règle des signes par le tableau suivant :
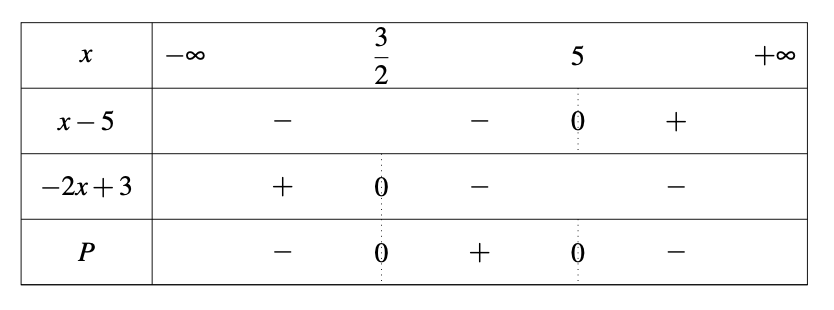
• Conclusion : puisque l'on veut que \(\displaystyle \left(x-5\right)\left(-2x+3\right) > 0\), les solutions sont dans l'intervalle \(\displaystyle \left]\frac{3}{2};5\right[\).
5) Les inéquations du type « quotient nul »
Pour résoudre une telle inéquation, on déterminer le signe du numérateur et du dénominateur puis on applique la règle des signes sur le quotient. L'idéal est de réaliser l'étude à l'aide d'un tableau de signes :
Exemple : Considérons l'inéquation \(\displaystyle \frac{-3x+6}{x-1} \leqslant 0\). L'étude se réalise de la façon suivante :
• le premier facteur \(\displaystyle -3x+6\) est une fonction affine qui s'annule en \(\displaystyle x=2\). Elle est décroissante car \(\displaystyle m < 0\). Elle sera positive sur \(\displaystyle \left]-\infty;2\right]\) et négative sur \(\displaystyle \left[2;+\infty\right[\).
• le deuxième facteur \(\displaystyle x-1\) est une fonction affine qui s'annule en \(\displaystyle x=1\). Elle est croissante car \(\displaystyle m > 0\). Elle sera négative sur \(\displaystyle \left]-\infty;1\right]\) et positive sur \(\displaystyle \left[1;+\infty\right[\).
• la valeur \(\displaystyle x=2\) est appelée la valeur charnière alors que la valeur \(\displaystyle x=1\) est appelée la valeur interdite car le dénominateur ne doit pas être nul.
• On résulme l'étude avec l'application de la règle des signes par le tableau suivant :
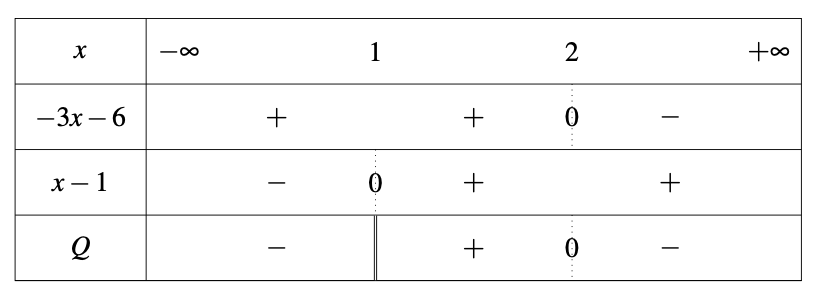
• Conclusion : puisque l'on veut que \(\displaystyle \frac{-3x+6}{x-1} \leqslant 0\), les solutions sont dans l'intervalle \(\displaystyle \left]-\infty;1\right[\cup\left[2;+\infty\right[\).