I) Mise en situation
Nous avons vu dans les séquences précédentes la nécessité d'étudier une situation à l'aide d'une fonction. Cette dernière était tracé dans un système de repérage que nous appelions un repère muni d'une origine et un système de graduation.
Dans la précédente séquence, nous avions démmaré avec la situation d'un lancé de projectile pour obtenir l'équation de la trajectoire à l'aide des lois de la physique. Cette étude peut être poussée en regardant plus particulièrement la vitesse en chaque point de la trajectoire.
Pour cela, il est utile de procéder à la géométrie dite analytique qui consister à utiliser les objets géométriques via un système de repérage. Nous devons alors concevoir par exemple le vecteur vitesse avec un système de repérage : les coordonnées, comme l'illustre la figure suivante :
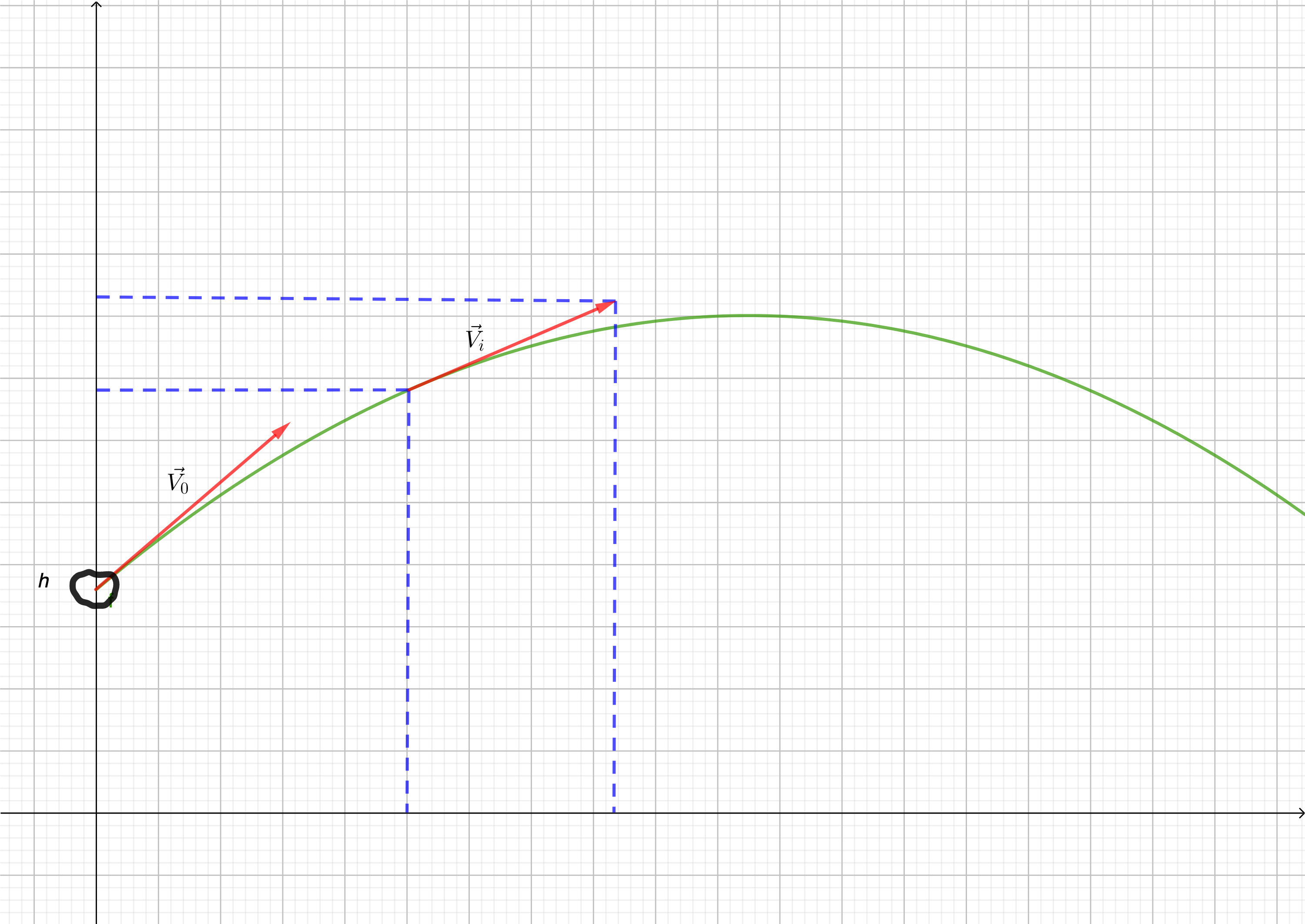
La projection du vecteur sur les deux axes nous donne les coordonnées du vecteur. Ainsi, des définitions et des propriétés s'imposent pour élaborer cette étude. C'est l'objectif de cette séquence.
On propose l'activité n°8 pour commencer la séquence.
II) Propriétés du vecteur par les coordonnées
Pour découvrir les propriétés d'un vecteur selon ses coordonnées, on définit d'abord le système de repérage.
1) Le système de repérage
Le système de repérage est déjà vu depuis la classe de 5ème. Il est construit avec deux axes sécants pour former l'origine. Le plus souvent, ces deux axes sont perpendiculaires. On dit alors que le repère formé est orthogonal.
A ce repère, on définit une base qui détermine les graduations. Pour cela, on utilise deux points \(\displaystyle I\) et \(\displaystyle J\) pour déterminer la première graduation censée représenter l'unité. Un tel repère est noté \(\displaystyle \left(O;I;J\right)\). Lorsque \(\displaystyle OI=OJ\), le repère est dit normé.
Ainsi, et ce sera souvent le cas, le repère le plus couramment employé est le repère orthonormé : deux axes perpendiculaires avec des graduations identiques.
2) Les coordonnées d'un vecteur
Les coordonnées d'un vecteur sont obtenues de la façon suivante :
Définition : Un vecteur \(\displaystyle \overrightarrow{AB}\) formé par les points \(\displaystyle A\) et \(\displaystyle B\) de coordonnées respectives \(\displaystyle A\left(x_A;y_A\right)\) et \(\displaystyle B\left(x_B;y_B\right)\) sont notées \(\displaystyle \overrightarrow{AB}\left(x_{AB};y_{AB}\right)\) ou \(\displaystyle \overrightarrow{AB}\begin{pmatrix} x_{AB} \\ y_{AB}\\ \end{pmatrix}\) telles que \(\displaystyle x_{AB}=x_B-x_A\) et \(\displaystyle y_{AB}=y_B-y_A\).
Exemple : Si un point \(\displaystyle A\) a pour coordonnées \(\displaystyle A\left(-3;4\right)\) et si un point \(\displaystyle B\) a pour coordonnées \(\displaystyle B\left(2;-1\right)\), alors le vecteur \(\displaystyle \overrightarrow{AB}\) formé par les deux points a pour coordonnées :
\(\displaystyle \begin{align*} \begin{pmatrix} x_{AB}&=x_B-x_A \\ y_{AB}&=y_B-y_A \\ \end{pmatrix} \\ \begin{pmatrix} x_{AB}&=2-\left(-3\right) \\ y_{AB}&=-1-4 \\ \end{pmatrix} \\ \begin{pmatrix} x_{AB}&=5 \\ y_{AB}&=-5 \\ \end{pmatrix} \\ \end{align*} \)
Remarque : En sciences, on a tendance de plus en plus d'écrire les coordonnées d'un vecteur sous forme de colonne plutôt qu'en ligne. On préfèrera donc la notation \(\displaystyle \overrightarrow{AB}\begin{pmatrix} 5 \\ -5\\ \end{pmatrix}\) plutôt que \(\displaystyle \overrightarrow{AB}\left(5;-5\right)\).
3) La norme d'un vecteur
La norme d'une vecteur est définie comme la distance entre les deux points d'extrémité du vecteur. Elle se calcule de la façon suivante :
Propriété : La norme d'un vecteur \(\displaystyle \overrightarrow{AB}\) est notée \(\displaystyle \left\|\overrightarrow{AB}\right\|\) et se calcule par \(\displaystyle \left\|\overrightarrow{AB}\right\|=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}\).
Exemple : Si un point \(\displaystyle A\) a pour coordonnées \(\displaystyle A\left(-3;4\right)\) et si un point \(\displaystyle B\) a pour coordonnées \(\displaystyle B\left(2;-1\right)\), alors le vecteur \(\displaystyle \overrightarrow{AB}\) formé par les deux points a pour norme :
\(\displaystyle \begin{align*} \left\|\overrightarrow{AB}\right\|&=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2} \\ &=\sqrt{\left(2+3\right)^2+\left(-1-4\right)^2} \\ &=\sqrt{5^2+\left(-5\right)^2} \\ &=\sqrt{25+25} \\ &=5\sqrt{2} \\ \end{align*} \)
Démonstration : Par définition, la norme d'un vecteur \(\displaystyle \overrightarrow{OM}\) de coordonnées \(\displaystyle \overrightarrow{OM}\begin{pmatrix} x_{OM} \\ y_{OM}\\ \end{pmatrix}\) est la longueur \(\displaystyle OM\).
En notant \(\displaystyle H\) le projeté orthogonal de \(\displaystyle M\) sur l'axe des abscisses et en notant \(\displaystyle P\), le projeté orthogonal de \(\displaystyle M\) sur l'axe des ordonnées, on obtient deux triangles rectangles \(\displaystyle OMH\) et \(\displaystyle OMP\).
A l'aide du théorème de Pythagore, on peut écrire que \(\displaystyle OM^2=OH^2+HM^2\). Ce qui devient \(\displaystyle OM^2=OH^2+OP^2\). Comme \(\displaystyle OH=x_{OM}\) et \(\displaystyle OP=y_{OM}\), alors on a \(\displaystyle OM^2=x_{OM}^2+y_{OM}^2\) d'où \(\displaystyle OM=\sqrt{x_{OM}^2+y_{OM}^2}\).
Ainsi, \(\displaystyle \left\|\overrightarrow{OM}\right\|=\sqrt{x_{OM}^2+y_{OM}^2}\)
4) Le milieu d'un segment
Les coordonnées du milieu d'un segment se calcule de la façon suivante :
Propriété : Les coordonnées du milieu \(\displaystyle I\) d'un segment \(\displaystyle \left[AB\right]\) se calculent par \(\displaystyle I\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right)\).
Exemple : Si un point \(\displaystyle A\) a pour coordonnées \(\displaystyle A\left(-3;4\right)\) et si un point \(\displaystyle B\) a pour coordonnées \(\displaystyle B\left(2;-1\right)\), alors le segment \(\displaystyle \left[AB\right]\) formé par les deux points a pour milieu le point \(\displaystyle I\) dont les coordonnées se calculent par :
\(\displaystyle \begin{align*} I&\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right) \\ I&\left(\frac{-3+2}{2};\frac{4-1}{2}\right) \\ I&\left(\frac{-1}{2};\frac{3}{2}\right) \\ \end{align*} \)
Démonstration : Le milieu \(\displaystyle I\) du segment \(\displaystyle \left[AB\right]\) est défini par \(\displaystyle \overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}\).
En écrivant l'égalité des coordonnées de ces vecteurs, on a : \(\displaystyle x_I-x_A=\frac{1}{2}\left(x_B-x_A\right)\) et \(\displaystyle y_I-y_A=\frac{1}{2}\left(y_B-y_A\right)\). Donc \(\displaystyle x_I=x_A+\frac{1}{2}\left(x_B-x_A\right)\) et \(\displaystyle y_I=y_A+\frac{1}{2}\left(y_B-y_A\right)\).
Ce qui donne finalement \(\displaystyle x_I=\frac{1}{2}\left(x_A+x_B\right)\) et \(\displaystyle y_I=\frac{1}{2}\left(y_A+y_B\right)\).
III Applications
Il existe une multitude d'applications qui font intervenir les coordonnées d'objets géométriques dans un repère. En classe de 2nde, nous en traitons quelques unes :
1) Le déterminant de deux vecteurs
Le déterminant de deux vecteurs est un nombre qui permet de déduire des résultats liés à la configuration géométrique. Il est définit de la façon suivante :
Définition : On considère deux vecteurs \(\displaystyle \overrightarrow{u}\begin{pmatrix} x \\ y\\ \end{pmatrix}\) et \(\displaystyle \overrightarrow{v}\begin{pmatrix} x' \\ y'\\ \end{pmatrix}\). Le déterminant de \(\displaystyle \overrightarrow{u}\) et \(\displaystyle \overrightarrow{v}\), noté \(\displaystyle \det\left(\overrightarrow{u};\overrightarrow{v}\right)\) est le nombre \(\displaystyle \det\left(\overrightarrow{u};\overrightarrow{v}\right)=\begin{vmatrix} x & x'\\ y & y'\end{vmatrix}\) avec \(\displaystyle \begin{vmatrix} x & x'\\ y & y'\end{vmatrix}=xy'-yx'\).
Exemple : Si un vecteur \(\displaystyle \overrightarrow{u}\) a pour coordonnées \(\displaystyle \overrightarrow{u}\begin{pmatrix} -1 \\ 3\\ \end{pmatrix}\) et si un vecteur \(\displaystyle \overrightarrow{v}\) a pour coordonnées \(\displaystyle \overrightarrow{v}\begin{pmatrix} 4 \\ 5\\ \end{pmatrix}\), alors le déterminant des deux vecteurs donne :
\(\displaystyle \begin{align*} det\left(\overrightarrow{u};\overrightarrow{v}\right)&=\begin{vmatrix}x&x'\\y&y'\end{vmatrix} \\ &=\begin{vmatrix}-1&4\\3&5\end{vmatrix} \\ &=-1\times5-4\times3 \\ &=-5-12 \\ &=-17 \end{align*} \)
Remarque : L'ordre des vecteurs est important : \(\displaystyle det\left(\overrightarrow{u};\overrightarrow{v}\right)=-det\left(\overrightarrow{v};\overrightarrow{u}\right)\).
2) La colinéarité
Dans la séquence sur les vecteurs, nous avions vu que deux vecteurs \(\displaystyle \overrightarrow{u}\) et \(\displaystyle \overrightarrow{v}\) sont colinéaires lorsqu'il existe un réel \(\displaystyle k\) tel que \(\displaystyle \overrightarrow{u}=k\overrightarrow{v}\). Avec le système de coordonnées, on obtient la propriété suivante :
Propriété : Deux vecteurs \(\displaystyle \overrightarrow{u}\) et \(\displaystyle \overrightarrow{v}\) sont colinéaires lorsque \(\displaystyle \det\left(\overrightarrow{u};\overrightarrow{v}\right)=0\).
Exemple : Si un vecteur \(\displaystyle \overrightarrow{u}\) a pour coordonnées \(\displaystyle \overrightarrow{u}\begin{pmatrix} -1 \\ 3\\ \end{pmatrix}\) et si un vecteur \(\displaystyle \overrightarrow{v}\) a pour coordonnées \(\displaystyle \overrightarrow{v}\begin{pmatrix} 4 \\ -12\\ \end{pmatrix}\), alors le déterminant des deux vecteurs donne :
\(\displaystyle \begin{align*} det\left(\overrightarrow{u};\overrightarrow{v}\right)&=\begin{vmatrix} x & x' \\ y & y' \end{vmatrix} \\ &=\begin{vmatrix}-1&4\\3&-12\end{vmatrix} \\ &=-1\times\left(-12\right)-4\times3 \\ &=12-12 \\ &=0 \end{align*} \)
On arrive bien à \(\displaystyle \det\left(\overrightarrow{u};\overrightarrow{v}\right)=0\) : les deux vecteurs \(\displaystyle \overrightarrow{u}\) et \(\displaystyle \overrightarrow{v}\) sont colinéaires.
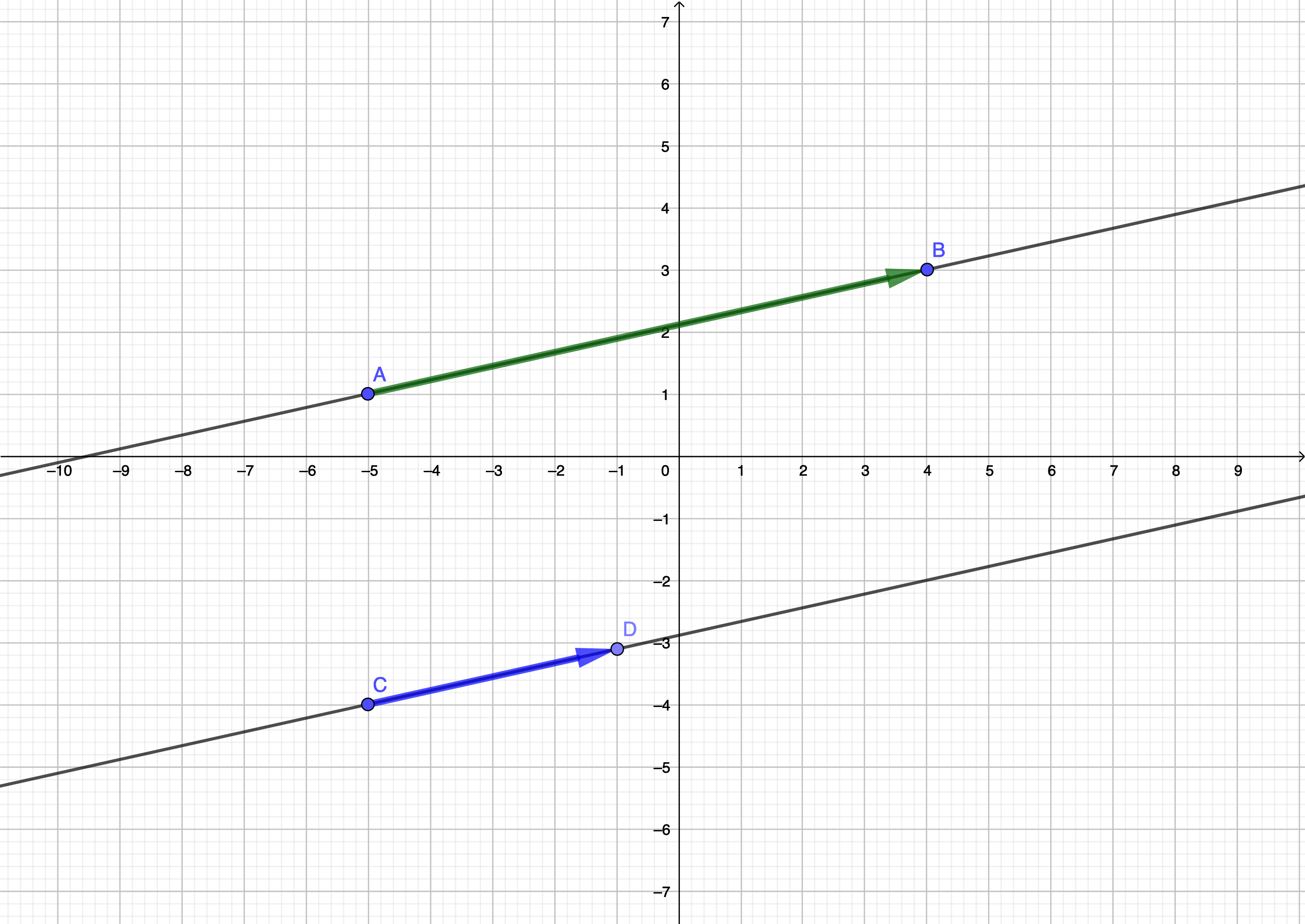
3) Le parallélisme
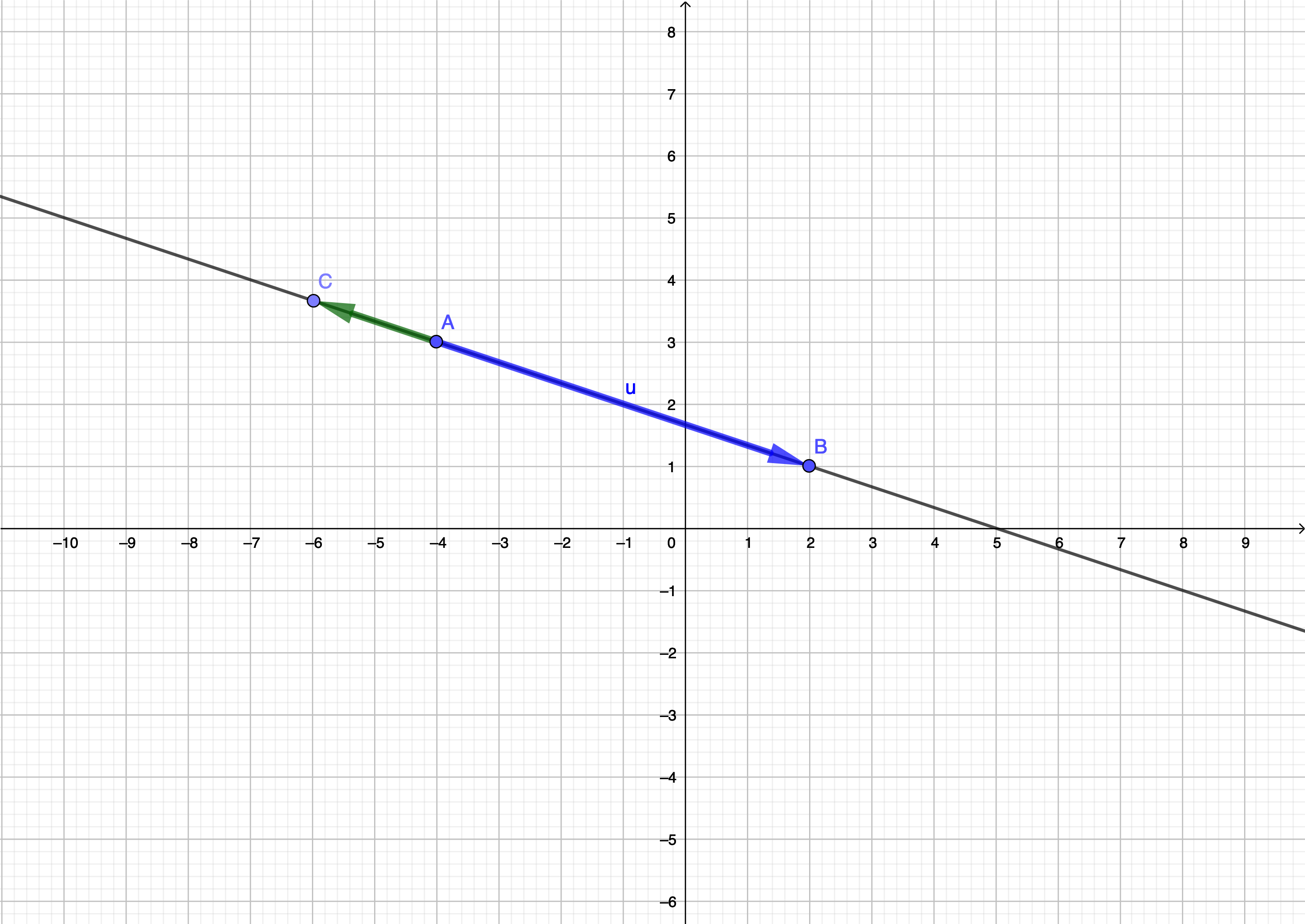
Le vecteur que deux vecteurs soient colinéaires impliquent que leur direction soient parallèles. Ainsi, deux droites \(\displaystyle \left(AB\right)\) et \(\displaystyle \left(CD\right)\) sont parallèles si et seulement si \(\displaystyle \overrightarrow{AB}\) et \(\displaystyle \overrightarrow{CD}\) sont colinéiares ou encore que \(\displaystyle \det\left(\overrightarrow{AB};\overrightarrow{CD}\right)=0\).
De la même façon, trois points \(\displaystyle A\) , \(\displaystyle B\) et \(\displaystyle C\) sont alignés si et seulement si \(\displaystyle \overrightarrow{AB}\) et \(\displaystyle \overrightarrow{AC}\) sont colinéaires avec le point \(\displaystyle A\) en commun, ou encore que \(\displaystyle \det\left(\overrightarrow{AB};\overrightarrow{AC}\right)=0\).