I) Mise en situation
Dans la séquence n°4, nous avons vu les fonctions dans ses généralités et en particulier les études de variations.
Les fonctions qui ont été aperçues sont toutes construites à partir de fonctions usuelles de base, appelées fonctions de référence. Ce sont des fonctions de base, simple à étudier, qui vont permettre de construire d'autres fonctions plus élaborées, de la même façon que les briques participent à la construction d'un édifice.
Au niveau de la classe de 2nde, on compte sept fonctions de référence. Elles vont être étudiées en détail dans cette séquence et feront l'objet d'un catalogue de fonctions de référence, qui sera complété ensuite en classe de première et de terminale.
Pour introduire l'étude d'une d'entre elles, on se propose d'étudier la trajectoire d'un projectile en fonction de l'angle de tir. L'activité n°7 permet de distinguer les différents cas.
II) La fonction constante
La fonction constante est définie de la façon suivante :
Définition : La fonction constante est définie sur \(\displaystyle \mathbb{R}\) par \(\displaystyle f\left(x\right)=c\), avec un \(\displaystyle c\) un nombre réel. Sa courbe représentative est une droite d'équation \(\displaystyle y=c\).
A titre d'exemple, on trace sur le graphique suivant deux fonctions constantes notées \(\displaystyle f\) et \(\displaystyle g\) telles que \(\displaystyle f\left(x\right)=2\) et \(\displaystyle g\left(x\right)=-3\) :
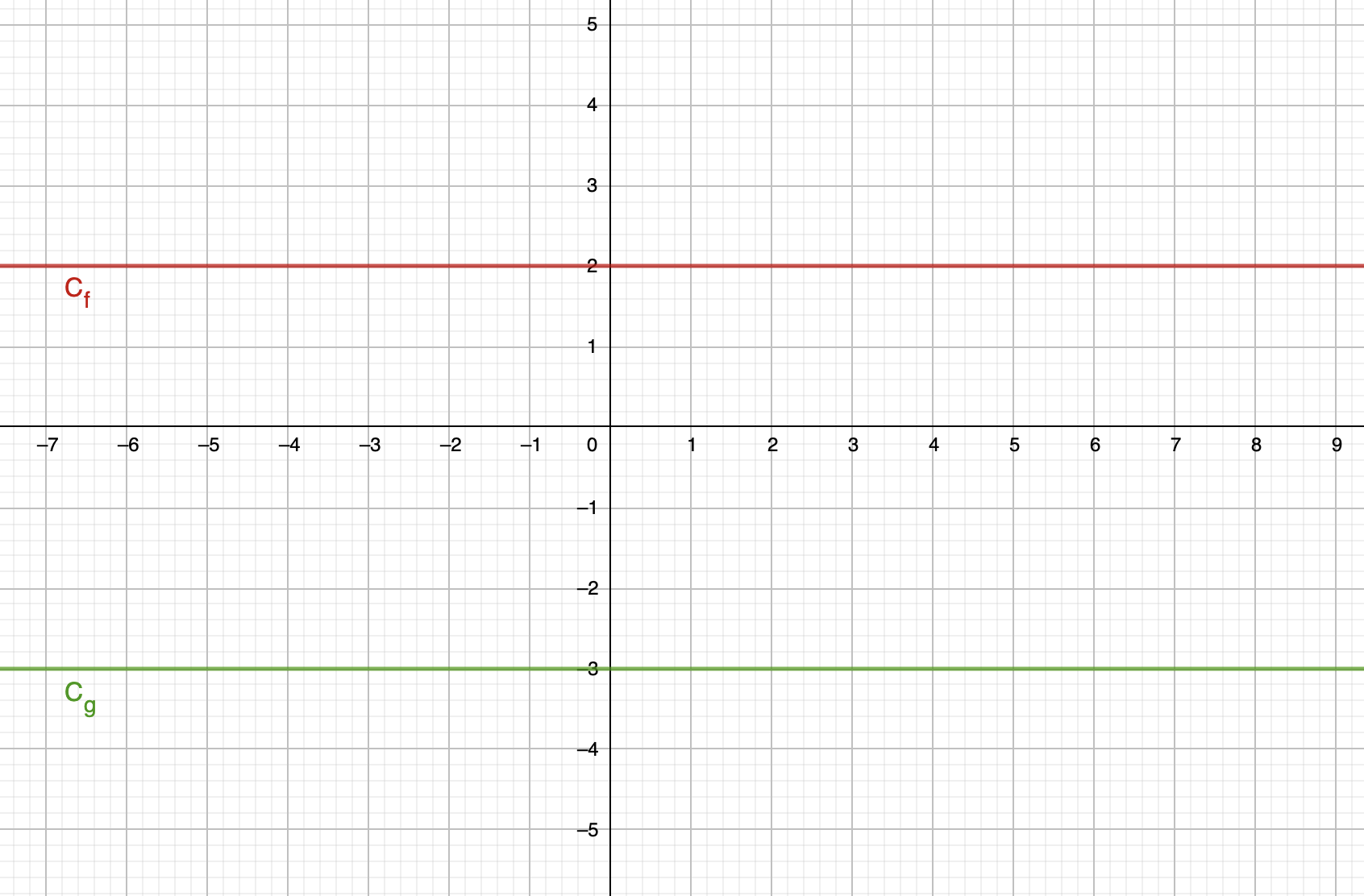
La fonction constante est paire sur un intervalle symétrique car quelques soient les valeurs de \(\displaystyle x\) sur cet intervalle, on a \(\displaystyle f\left(x\right)=f\left(-x\right)\).
III) La fonction linéaire
La fonction linéaire est définie de la façon suivante :
Définition : La fonction linéaire est définie sur \(\displaystyle \mathbb{R}\) par \(\displaystyle f\left(x\right)=mx\), avec un \(\displaystyle m\) un nombre réel. Sa courbe représentative est une droite d'équation \(\displaystyle y=mx\).
A titre d'exemple, on trace sur le graphique suivant deux fonctions liénaires notées \(\displaystyle f\) et \(\displaystyle g\) telles que \(\displaystyle f\left(x\right)=2x\) et \(\displaystyle g\left(x\right)=\frac{-1}{3}x\) :
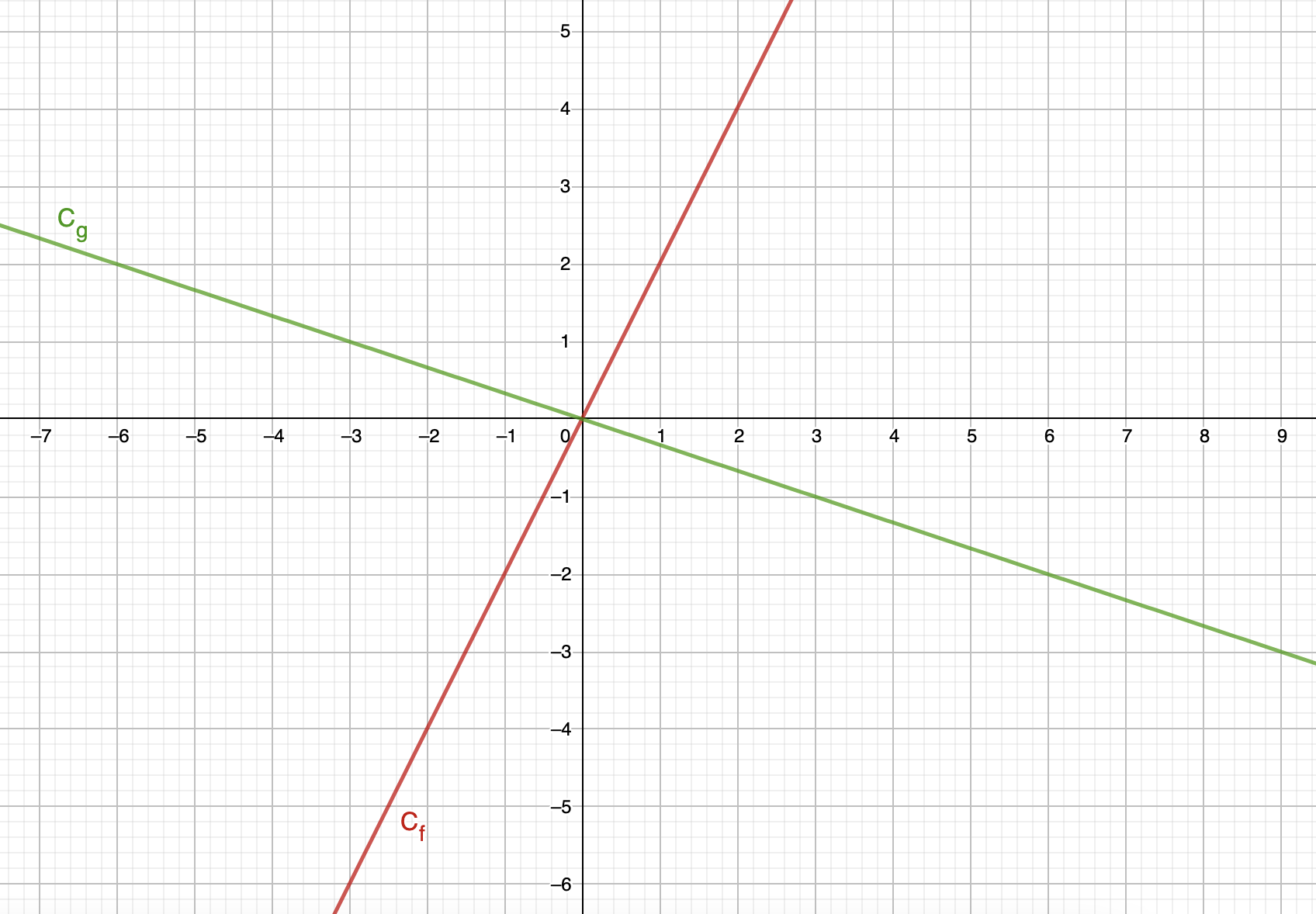
La fonction linéaire est impaire sur un intervalle symétrique car quelques soient les valeurs de \(\displaystyle x\) sur cet intervalle, on a \(\displaystyle f\left(x\right)=-f\left(-x\right)\).
La courbe représentative d'une fonction linéaire est une droite qui passe par l'origine du repère.
Pour une telle fonction, on définit le taux d'accroissement :
Définition : Soit une fonction \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\). Pour touts nombres réels \(\displaystyle x_1\) et \(\displaystyle x_2\) distincts dans \(\displaystyle I\), on appelle taux d'accroissement de \(\displaystyle f\) entre \(\displaystyle x_1\) et \(\displaystyle x_2\), le quotient \(\displaystyle \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}\).
Le calcul de ce taux de variations est similaire au calcul du coefficient directeur \(\displaystyle m\) de la droite. Si on a deux points de cette droite \(\displaystyle A\) et \(\displaystyle B\) tels que les coordonnées soient \(\displaystyle A\left(a;f\left(a\right)\right)\) et \(\displaystyle B\left(b;f\left(b\right)\right)\) alors le taux d'acroissement devient \(\displaystyle \frac{f\left(b\right)-f\left(a\right)}{b-a}\) ou encore \(\displaystyle \frac{y_B-y_A}{x_B-x_A}\) et ce n'est autre que le coefficient directeur \(\displaystyle m\) :
Propriété : Soit une fonction linéaire \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\) par \(\displaystyle f\left(x\right)=mx\). Le taux d'acroissement de la fonction est le réel \(\displaystyle m\), appelé le coefficient directeur de la droite \(\displaystyle \left(C_f\right)\) représentative de \(\displaystyle f\).
Propriété : Soit une fonction linéaire \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\) par \(\displaystyle f\left(x\right)=mx\). Si \(\displaystyle m > 0\) alors la fonction est croissante sur \(\displaystyle I\) et si \(\displaystyle m < 0\) alors \(\displaystyle f\) est décroissante sur \(\displaystyle I\).
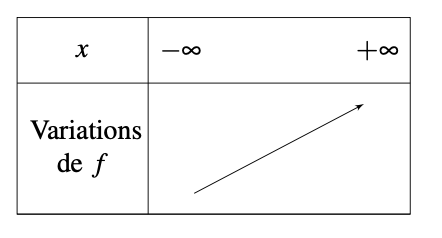
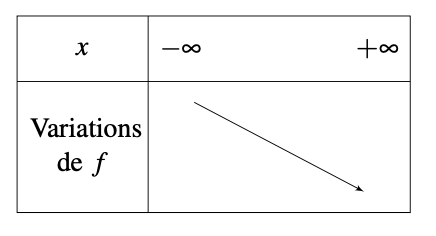
Démonstration : On considère une fonction linéaire \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\) telle que \(\displaystyle f\left(x\right)=mx\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle m\times a < m\times b\) dans le cas où \(\displaystyle m > 0\). Ce qui correspond à \(\displaystyle f\left(a\right) < f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) < f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est croissante sur \(\displaystyle I\). La démonstration est analogue avec \(\displaystyle m < 0\).
Remarque : Si \(\displaystyle m > 0\), \(\displaystyle f\left(x\right) < 0\) sur \(\displaystyle \left]-\infty;0\right]\) et \(\displaystyle f\left(x\right) > 0\) sur \(\displaystyle \left[0;+\infty\right[\). De la même façon, si \(\displaystyle m < 0\), \(\displaystyle f\left(x\right) > 0\) sur \(\displaystyle \left]-\infty;0\right]\) et \(\displaystyle f\left(x\right) < 0\) sur \(\displaystyle \left[0;+\infty\right[\).
IV) La fonction affine
La fonction affine est définie de la façon suivante :
Définition : La fonction affine est définie sur \(\displaystyle \mathbb{R}\) par \(\displaystyle f\left(x\right)=mx+p\), avec un \(\displaystyle m\) et \(\displaystyle p\) deux nombres réels. Sa courbe représentative est une droite d'équation \(\displaystyle y=mx+p\).
A titre d'exemple, on trace sur le graphique suivant deux fonctions liénaires notées \(\displaystyle f\) et \(\displaystyle g\) telles que \(\displaystyle f\left(x\right)=2x-3\) et \(\displaystyle g\left(x\right)=\frac{-1}{2}x+2\) :
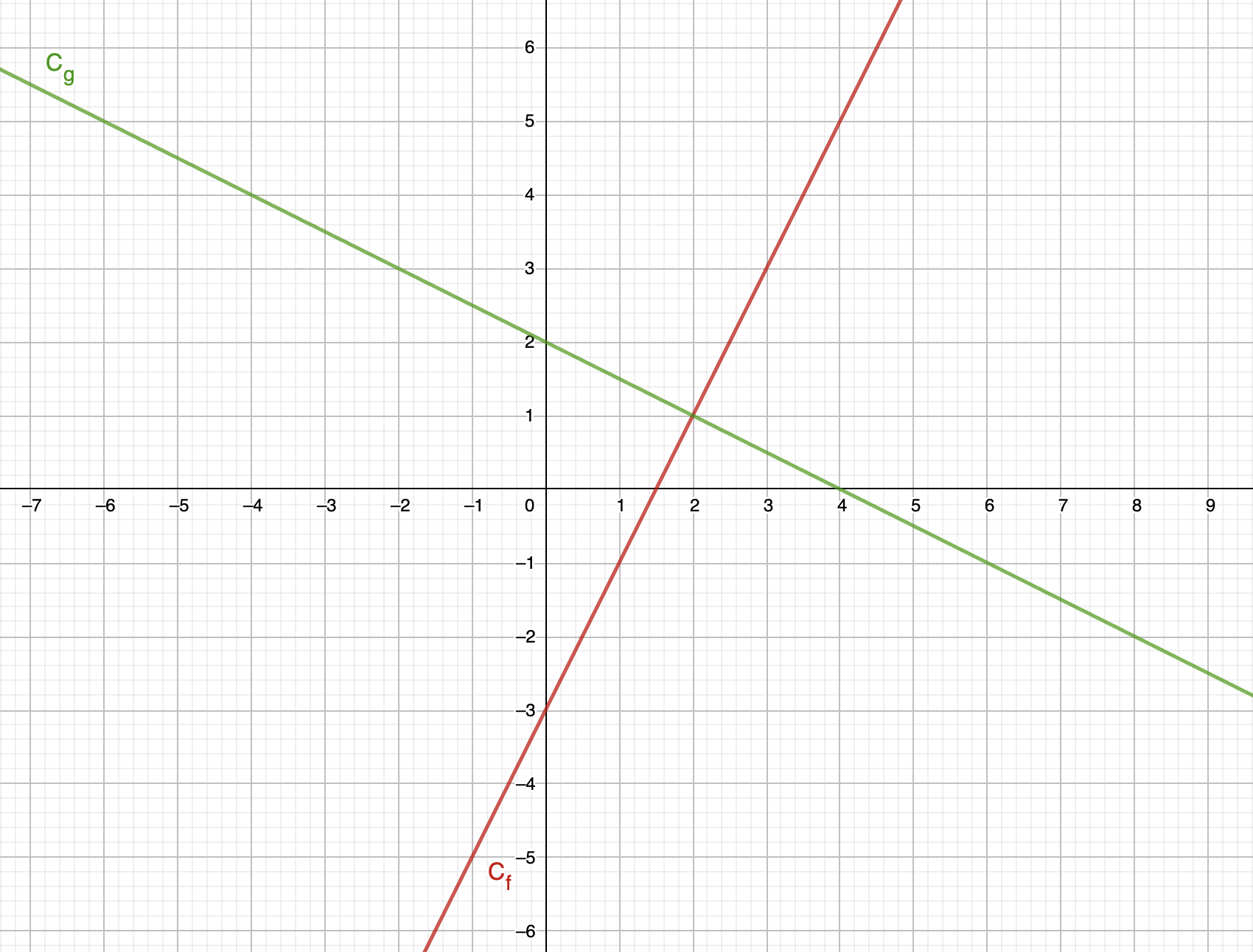
La fonction affine est ni paire, ni impaire.
La courbe représentative d'une fonction affine est une droite qui ne passe pas par l'origine du repère.
Pour une telle fonction, on définit le taux d'accroissement :
Définition : Soit une fonction \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\). Pour touts nombres réels \(\displaystyle x_1\) et \(\displaystyle x_2\) distincts dans \(\displaystyle I\), on appelle taux d'accroissement de \(\displaystyle f\) entre \(\displaystyle x_1\) et \(\displaystyle x_2\), le quotient \(\displaystyle \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}\).
Le calcul de ce taux de variations est similaire au calcul du coefficient directeur \(\displaystyle m\) de la droite. Si on a deux points de cette droite \(\displaystyle A\) et \(\displaystyle B\) tels que les coordonnées soient \(\displaystyle A\left(a;f\left(a\right)\right)\) et \(\displaystyle B\left(b;f\left(b\right)\right)\) alors le taux d'acroissement devient \(\displaystyle \frac{f\left(b\right)-f\left(a\right)}{b-a}\) ou encore \(\displaystyle \frac{y_B-y_A}{x_B-x_A}\) et ce n'est autre que le coefficient directeur \(\displaystyle m\) :
Propriété : Soit une fonction affine \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\) par \(\displaystyle f\left(x\right)=mx+p\). Le taux d'acroissement de la fonction est le réel \(\displaystyle m\), appelé le coefficient directeur de la droite \(\displaystyle \left(C_f\right)\) représentative de \(\displaystyle f\).
Propriété : Soit une fonction affine \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\) par \(\displaystyle f\left(x\right)=mx+p\). Si \(\displaystyle m > 0\) alors la fonction est croissante sur \(\displaystyle I\) et si \(\displaystyle m < 0\) alors \(\displaystyle f\) est décroissante sur \(\displaystyle I\).
Propriété : Soit une fonction affine \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\) par \(\displaystyle f\left(x\right)=mx+p\). Le réel \(\displaystyle p\) est l'ordonnée du point de la courbe d'abscisse \(\displaystyle x=0\). De ce fait, il est appelé l'ordonnée à l'origine.


Démonstration : On considère une fonction affine \(\displaystyle f\) définie sur un intervalle \(\displaystyle I\) telle que \(\displaystyle f\left(x\right)=mx+p\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle m\times a < m\times b\) dans le cas où \(\displaystyle m > 0\). Ensuite, \(\displaystyle m\times a +p < m\times b+p\). Ce qui correspond à \(\displaystyle f\left(a\right) < f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) < f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est croissante sur \(\displaystyle I\). La démonstration est analogue avec \(\displaystyle m < 0\).
Remarque : Si \(\displaystyle m > 0\), \(\displaystyle f\left(x\right) < 0\) sur \(\displaystyle \left]-\infty;\frac{-p}{m}\right]\) et \(\displaystyle f\left(x\right) > 0\) sur \(\displaystyle \left[\frac{-p}{m};+\infty;\frac{-p}{m}\right[\). De la même façon, si \(\displaystyle m < 0\), \(\displaystyle f\left(x\right) > 0\) sur \(\displaystyle \left]-\infty;\frac{-p}{m}\right]\) et \(\displaystyle f\left(x\right) < 0\) sur \(\displaystyle \left[\frac{-p}{m};+\infty;0\right[\).
V) La fonction carrée
La fonction carrée est définie de la façon suivante :
Définition : La fonction carrée est définie sur \(\displaystyle \mathbb{R}\) par \(\displaystyle f\left(x\right)=x^2\). Sa courbe représentative est une parabole qui a pour sommet l'origine du repère. La concavité de cette parabole est vers le haut.
La courbe représentative de la fonction carrée donne :
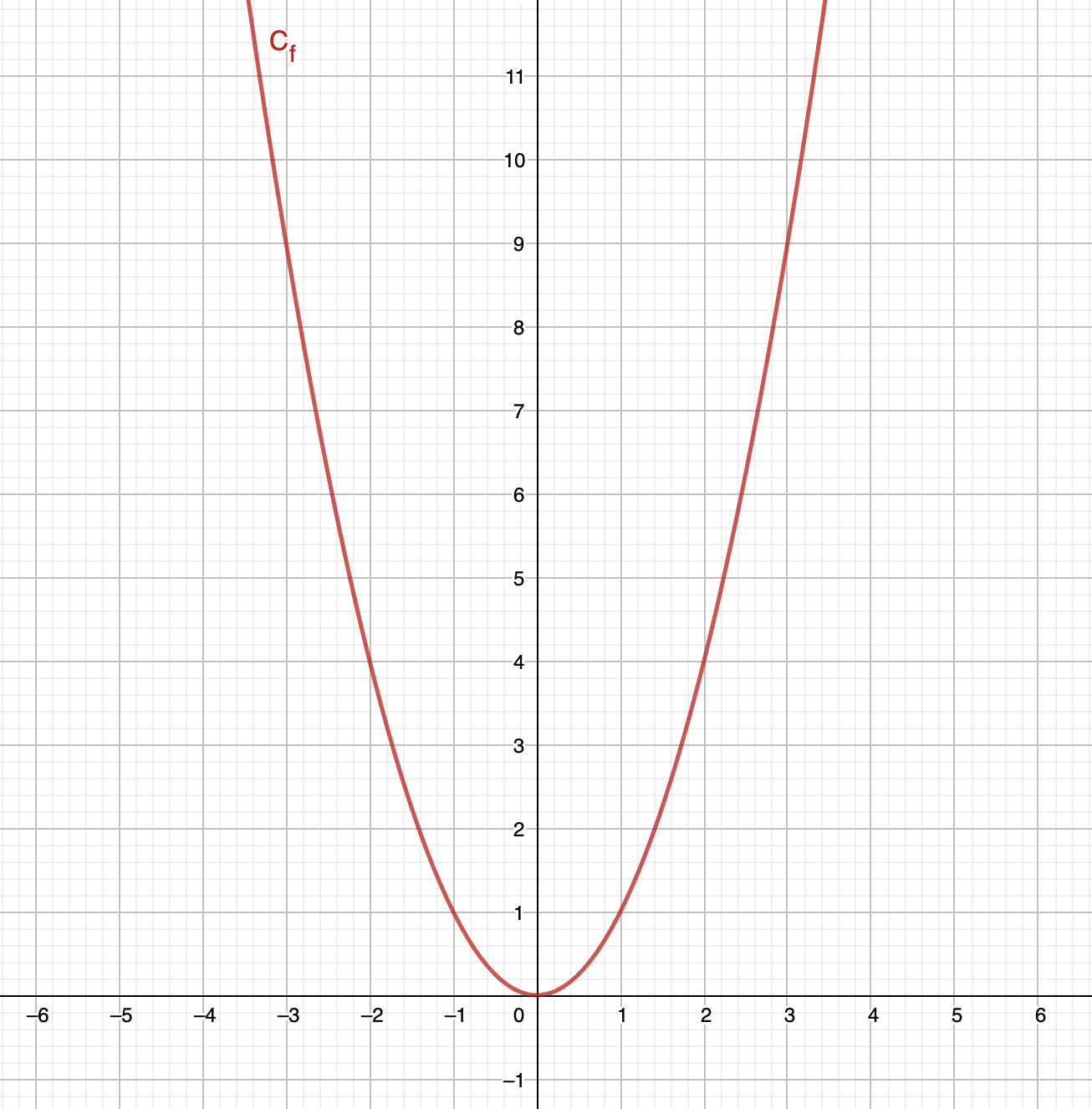
La fonction carrée est paire. Pour tout \(\displaystyle x\) d'un intervalle symétrique, on a \(\displaystyle x^2=\left(-x\right)^2\).
Propriété : La fonction carrée est strictement décroissante sur \(\displaystyle \left]-\infty;0\right]\) et strictement croissante sur \(\displaystyle \left[0;+\infty\right[\). Elle admet 0 comme minimum atteint en 0.
Les variations de la fonction carré sont résumées de la façon suivante :
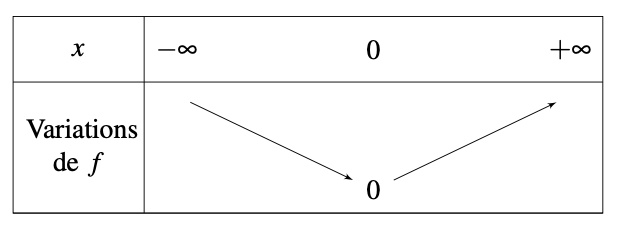
Démonstration : On considère la fonction carrée \(\displaystyle f\) définie sur un intervalle \(\displaystyle \left]-\infty;0\right]\) telle que \(\displaystyle f\left(x\right)=x^2\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle a^2 > b^2\) car \(\displaystyle a < b < 0\). Ce qui correspond à \(\displaystyle f\left(a\right) > f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) > f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est décroissante sur \(\displaystyle \left]-\infty;0\right]\).
Démonstration : On considère la fonction carrée \(\displaystyle f\) définie sur un intervalle \(\displaystyle \left[0;+\infty\right[\) telle que \(\displaystyle f\left(x\right)=x^2\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle a^2 < b^2\) car \(\displaystyle 0 < a < b \). Ce qui correspond à \(\displaystyle f\left(a\right) < f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) < f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est croissante sur \(\displaystyle \left[0;+\infty\right[\).
VI) La fonction cube
La fonction cube est définie de la façon suivante :
Définition : La fonction cube est définie sur \(\displaystyle \mathbb{R}\) par \(\displaystyle f\left(x\right)=x^3\).
La courbe représentative de la fonction cube donne :
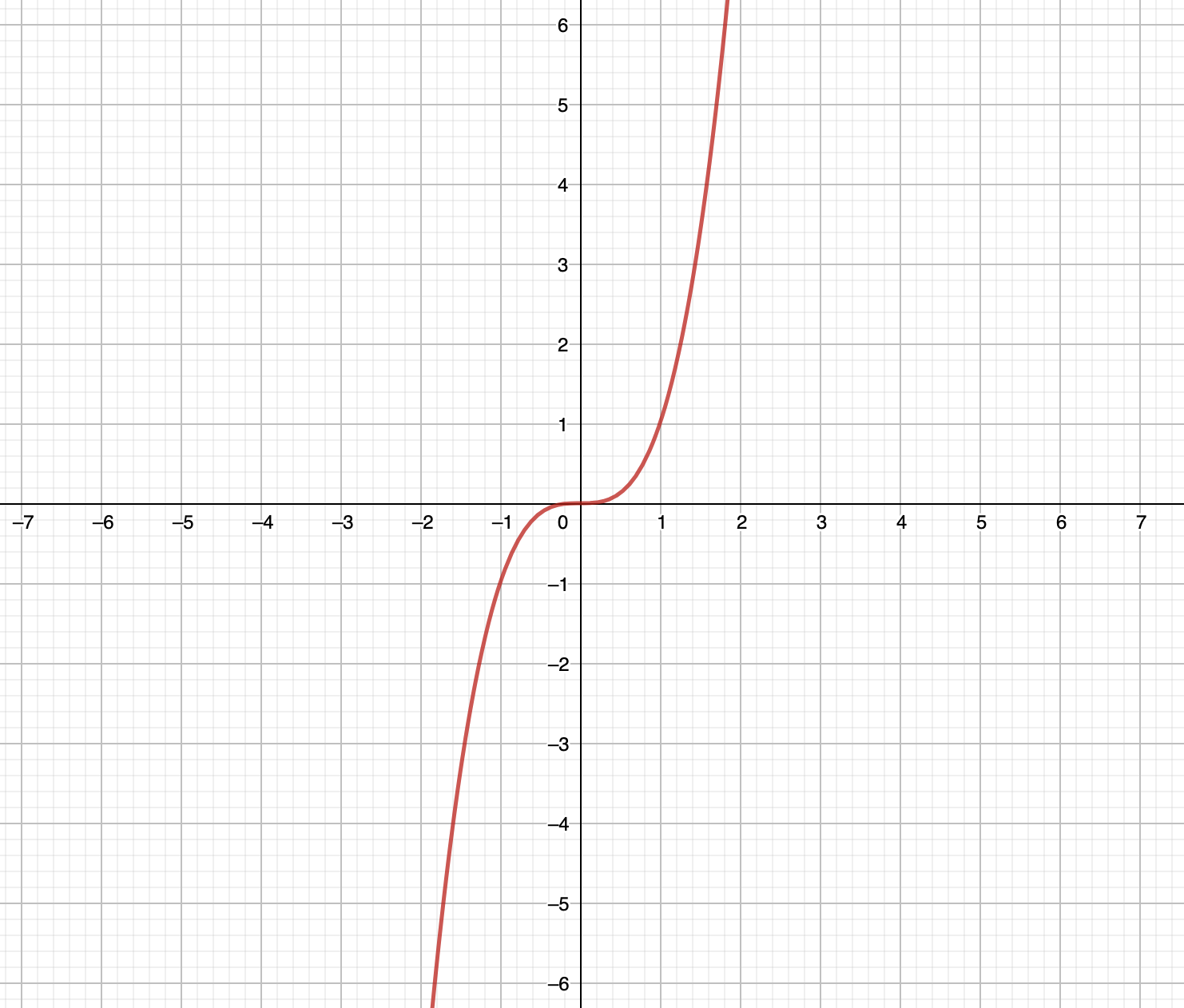
La fonction cube est impaire. Pour tout \(\displaystyle x\) d'un intervalle symétrique, on a \(\displaystyle x^3=-\left(-x\right)^3\).
Propriété : La fonction cube est strictement croissante sur \(\displaystyle \mathbb{R}\).
Les variations de la fonction cube sont résumées de la façon suivante :

Démonstration : On considère la fonction cube \(\displaystyle f\) définie sur un intervalle \(\displaystyle \left]-\infty;0\right]\) telle que \(\displaystyle f\left(x\right)=x^3\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle a^3 < b^3\) car \(\displaystyle a < b < 0\). Ce qui correspond à \(\displaystyle f\left(a\right) < f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) < f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est croissante sur \(\displaystyle \left]-\infty;0\right]\).
Démonstration : On considère la fonction cube \(\displaystyle f\) définie sur un intervalle \(\displaystyle \left[0;+\infty\right[\) telle que \(\displaystyle f\left(x\right)=x^3\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle a^3 < b^3\) car \(\displaystyle 0 < a < b \). Ce qui correspond à \(\displaystyle f\left(a\right) < f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) < f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est croissante sur \(\displaystyle \left[0;+\infty\right[\).
VII) La fonction inverse
La fonction inverse est définie de la façon suivante :
Définition : La fonction inverse est définie sur \(\displaystyle \left]-\infty;0\right[\cup\left]0;+\infty\right[\) noté aussi \(\displaystyle \mathbb{R}^{*}\) ou encore \(\displaystyle \mathbb{R} / \{0\}\)par \(\displaystyle f\left(x\right)=\frac{1}{x}\). La courbe représentative de la fonction inverse est une hyperbole qui admet pour centre, l'origine du repère.
La courbe représentative de la fonction inverse donne :
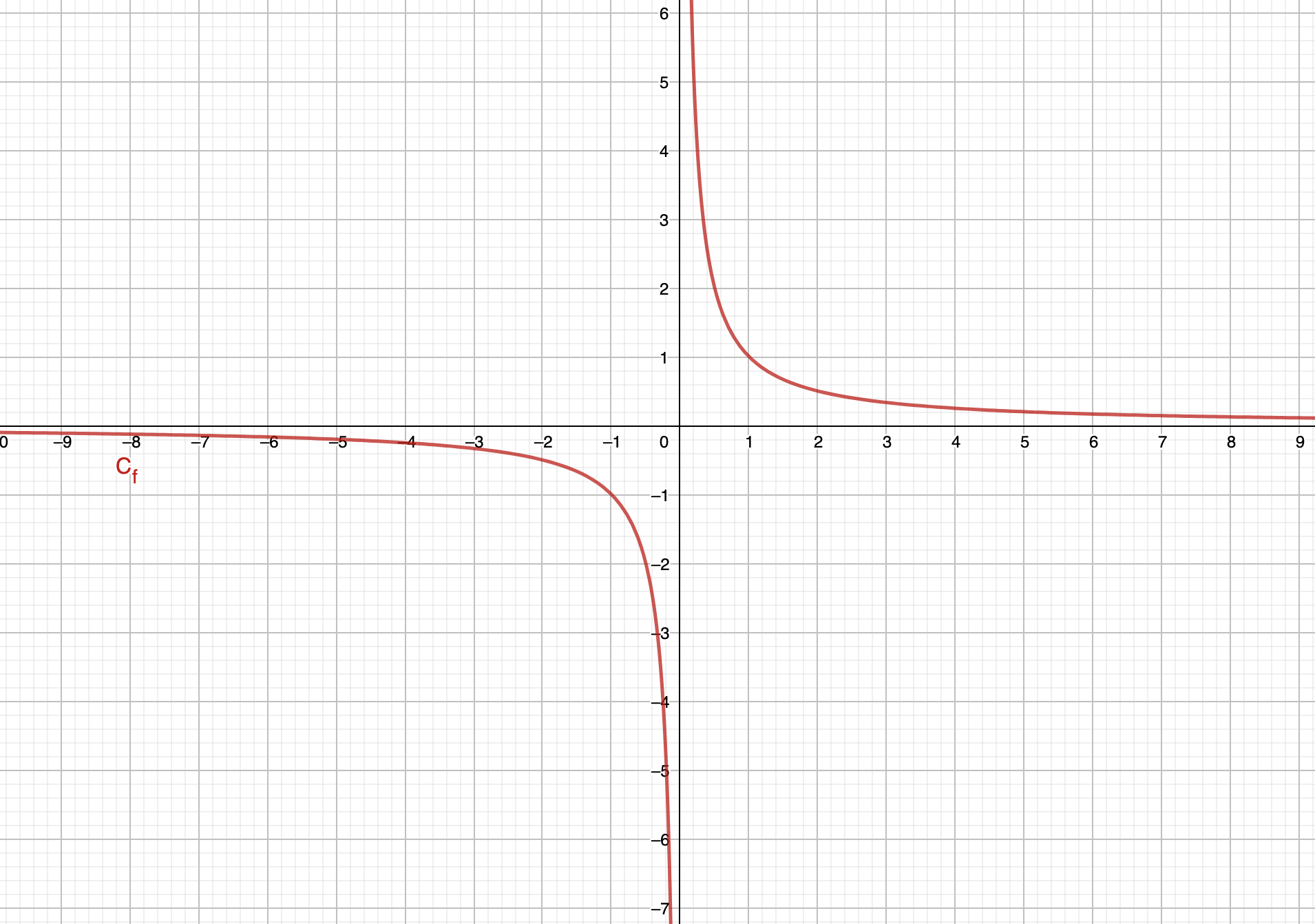
La fonction inverse est impaire. Pour tout \(\displaystyle x\) d'un intervalle symétrique, on a \(\displaystyle \frac{1}{x}=-\frac{1}{-x}\).
Propriété : La fonction inverse est strictement décroissante sur \(\displaystyle \left]-\infty;0\right[\) et strictement décroissante sur \(\displaystyle \left]0;+\infty\right[\).
Les variations de la fonction inverse sont résumées de la façon suivante :
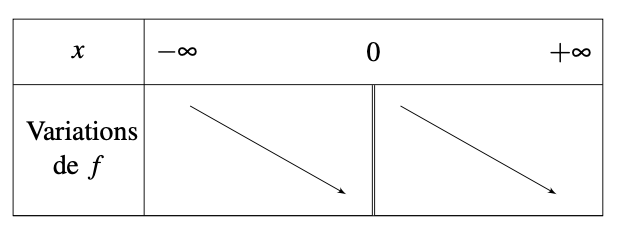
Le fait que la fonction admette la valeur interdite 0 est schématisé par une double bare verticale dans le tableau de variations.
Démonstration : On considère la fonction cube \(\displaystyle f\) définie sur un intervalle \(\displaystyle \left]-\infty;0\right[\) telle que \(\displaystyle f\left(x\right)=\frac{1}{x}\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle \frac{1}{a} > \frac{1}{b}\) car \(\displaystyle a < b < 0\). Ce qui correspond à \(\displaystyle f\left(a\right) > f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) > f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est décroissante sur \(\displaystyle \left]-\infty;0\right[\).
Démonstration : On considère la fonction cube \(\displaystyle f\) définie sur un intervalle \(\displaystyle \left]0;+\infty\right[\) telle que \(\displaystyle f\left(x\right)=\frac{1}{x}\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle \frac{1}{a} > \frac{1}{b}\) car \(\displaystyle 0 < a < b \). Ce qui correspond à \(\displaystyle f\left(a\right) > f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) > f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est décroissante sur \(\displaystyle \left]0;+\infty\right[\).
VIII) La fonction racine carrée
La fonction racine carrée est définie de la façon suivante :
Définition : La fonction racine carrée est définie sur \(\displaystyle \left[0;+\infty\right[\) noté aussi \(\displaystyle \mathbb{R}^{+}\)par \(\displaystyle f\left(x\right)=\sqrt{x}\).
La courbe représentative de la fonction racine carrée donne :
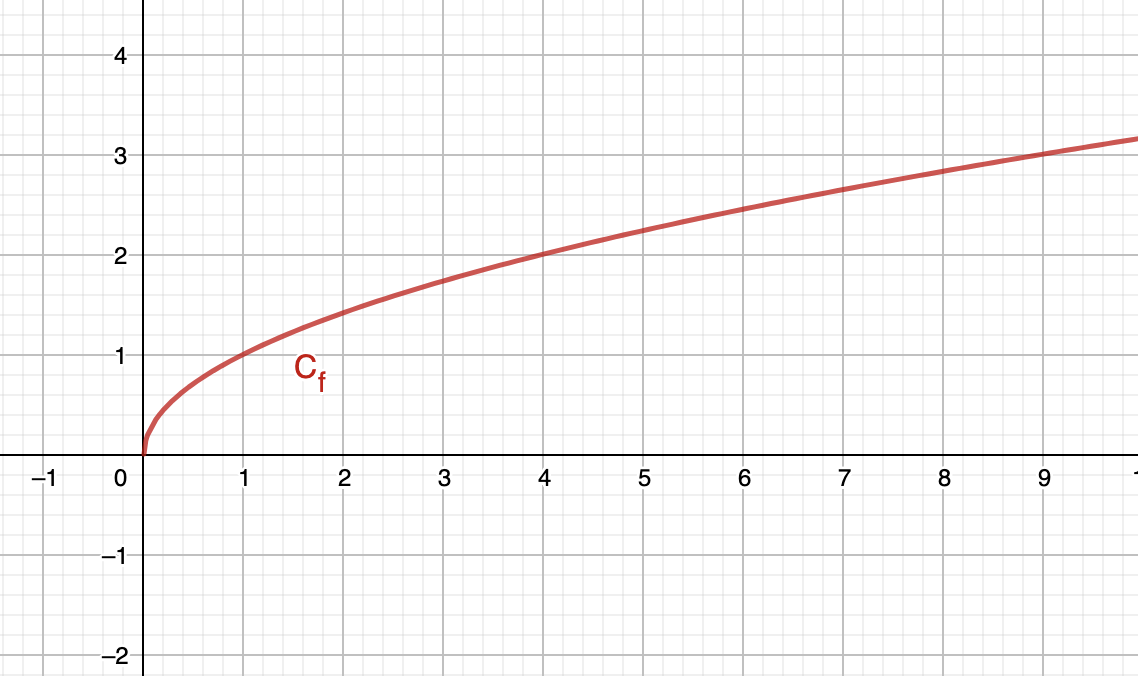
La fonction racine carrée est ni paire, ni impaire.
Propriété : La fonction racine carrée est strictement croissante sur \(\displaystyle \mathbb{R}^{+}\).
Les variations de la fonction racine carrée sont résumées de la façon suivante :
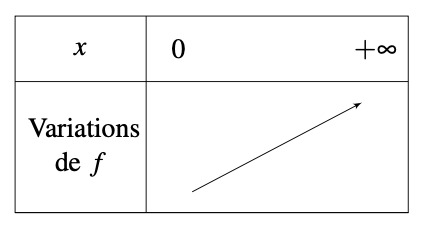
Démonstration : On considère la fonction cube \(\displaystyle f\) définie sur un intervalle \(\displaystyle \left[0;+\infty\right[\) telle que \(\displaystyle f\left(x\right)=\sqrt{x}\). On considère deux nombres \(\displaystyle a\) et \(\displaystyle b\) de \(\displaystyle I\) tels que \(\displaystyle a < b\). On a alors \(\displaystyle \sqrt{a} < \sqrt{b}\) car \(\displaystyle 0 < a < b \). Ce qui correspond à \(\displaystyle f\left(a\right) < f\left(b\right)\). Ainsi, comme \(\displaystyle f\left(a\right) < f\left(b\right)\) avec \(\displaystyle a < b\) alors la fonction \(\displaystyle f\) est croissante sur \(\displaystyle \left[0;+\infty\right[\).