I) Mise en situation
Dessiner un marteau écraser une ampoule est relativement facile. En revanche, il existe des phénomènes entre le marteau et l'ampoule qui sont difficiles à dessiner.

Par analogie avec une bande dessinée, la lecture ne peut pas donner toute l'information proposée par l'auteur. Par exemple, pour exprimer une joie, on va indiquer dans la bulle un Soleil, un coeur, des notes de musique, ... des symboles qui représentent cet état d'esprit. De la même façon, pour la colère, on verra apparaître des éclaires, des têtes de mort, etc.
Pour exprimer un mouvement, toujours sur un dessin, on peut simuler des traits qui permettent de simuler une vibration de l'objet ou du personnage qui bouge. On retrouve alors encore une fois toute une symbolique pour informer le lecteur d'une action.
En physique, on procède de la même façon. On utilise un symbole pour représenter une force. Ce symbole est un outil géométrique appelé vecteur. C'est un segment fléché :

Sur le plan mathématique, on peut aborder la notion de vecteur par la petite activité : activité n°6
II) La notion de vecteurs
A l'aide de ce qui précède, on peut définir le vecteur de la façon suivante :
1) Définition
On définit le vecteur de la façon suivante :
Définition : Un vecteur est un segment de droite orienté sur lequel on peut effectuer des opérations.
La représentation d'un vecteur est la suivante :
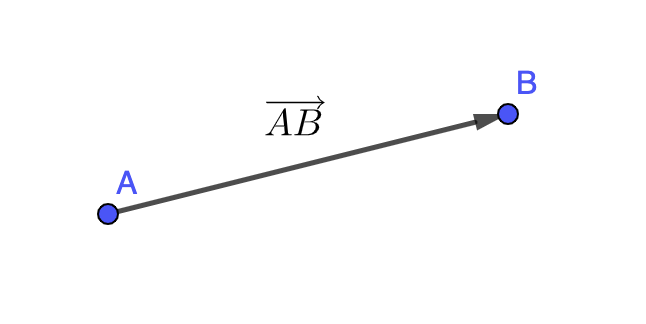
La notation du vecteur \(\displaystyle \overrightarrow{AB}\) se réalise en utilisant la lettre d'origine \(\displaystyle A\) et la lettre à l'extrémité \(\displaystyle B\). Il peut être noté aussi avec une simple lettre comme par exemple le vecteur \(\displaystyle \overrightarrow{u}\).
Le vecteur \(\displaystyle \overrightarrow{AB}\) est définit aussi selon une direction, un sens, une norme et son point d'application. Ce sont les caractéristiques du vecteurs.
Par convention, le vecteur \(\displaystyle \overrightarrow{AA}\) ayant une norme nulle, il est appelé vecteur nul et est noté \(\displaystyle \overrightarrow{0}\). Ce sont tous les vecteurs dont l'origine est confondue avec l'extrémité.
2) Les vecteurs dans la translation
La notion de vecteur apparait dans une transformation du plan : la translation.
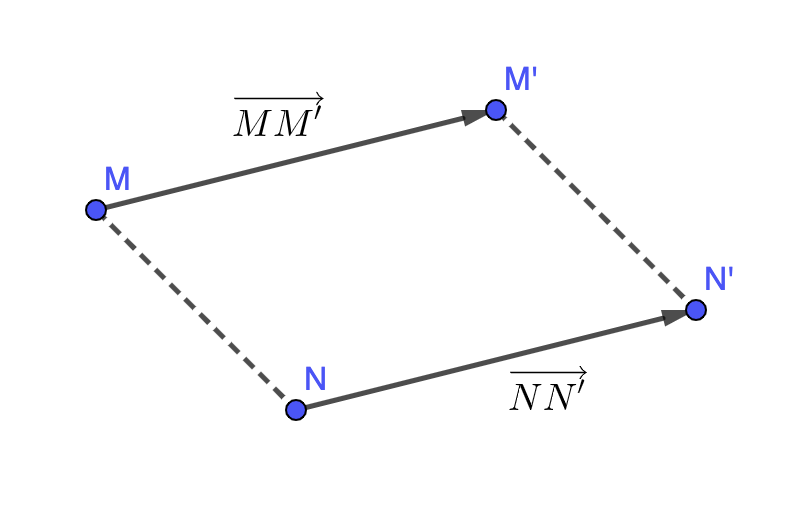
Définition : On considère deux points distincts du plan \(\displaystyle M\) et \(\displaystyle M'\). La translation qui transforme \(\displaystyle M\) en \(\displaystyle M'\) associe à tout point \(\displaystyle N\) du plan, l'unique point \(\displaystyle N'\) tel que \(\displaystyle MM’N’N\) soit un parallélogramme.
Cette transformation est caractérisée par un déplacement selon une direction, un sens et une longueur. Ici, la direction est la droite \(\displaystyle \left(MM'\right)\), le sens est de \(\displaystyle M\) vers \(\displaystyle M'\) et la la longueur est celle de \(\displaystyle MM'\).
Définition : La translation qui transforme \(\displaystyle M\) en \(\displaystyle M'\) est appelée la translation de vecteur \(\displaystyle \overrightarrow{MM'}\).
3) Les égalités de vecteurs
Une égalité de deux vecteurs amène aux deux définitions suivantes :
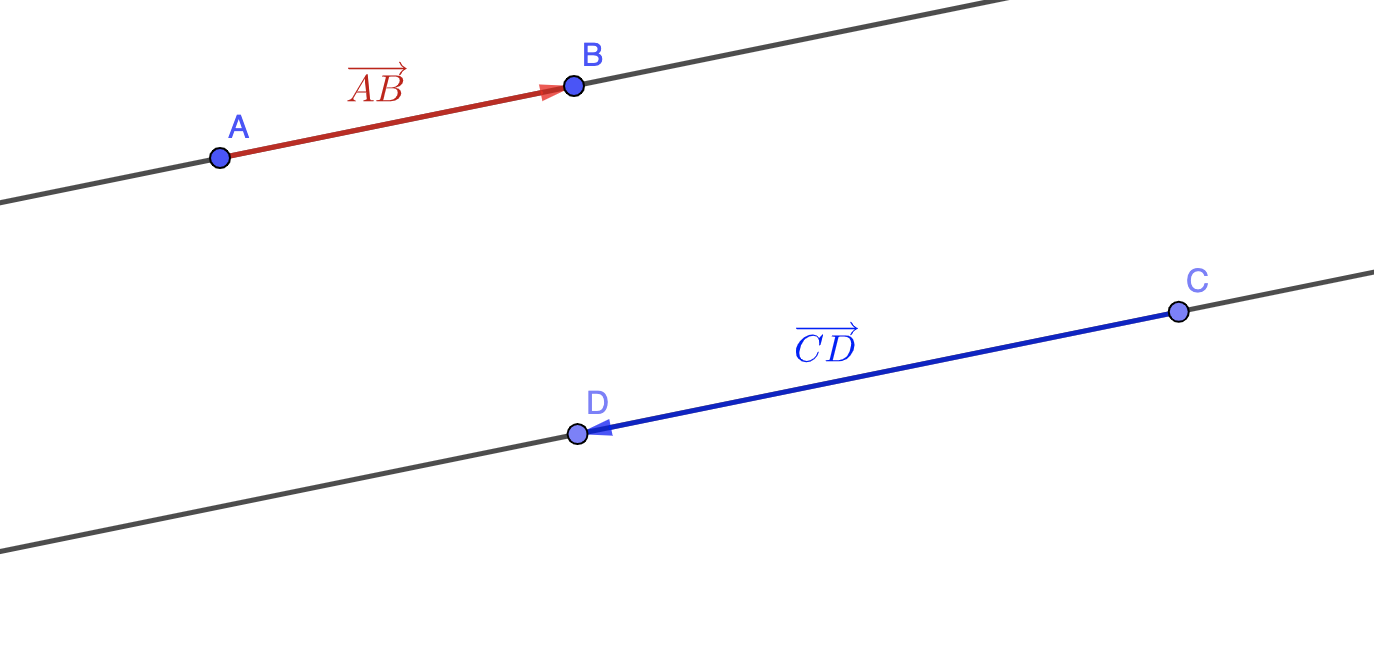
Définition : Deux vecteurs non nuls \(\displaystyle \overrightarrow{AB}\) et \(\displaystyle \overrightarrow{CD}\) sont égaux s'ils ont la même direction, le même sens et la même norme. On écrit alors \(\displaystyle \overrightarrow{AB}=\overrightarrow{CD}\).
Remarque : Cette égalité signifie que le point \(\displaystyle D\) est l'image du point \(\displaystyle C\) par la translation de vecteur \(\displaystyle \overrightarrow{AB}\).
Définition : Deux vecteurs non nuls \(\displaystyle \overrightarrow{AB}\) et \(\displaystyle \overrightarrow{CD}\) sont égaux si et seulement si le quadrilatère \(\displaystyle ABDC\) est parallélogramme.
Remarque 1 : L'égalité \(\displaystyle \overrightarrow{AB}=\overrightarrow{BC}\) équivaut à dire que \(\displaystyle B\) est le milieu de \(\displaystyle \left[AC\right]\).
Remarque 2 : Le vecteur \(\displaystyle \overrightarrow{AB}\) n'est pas unique. Il admet une infinité de représentants :
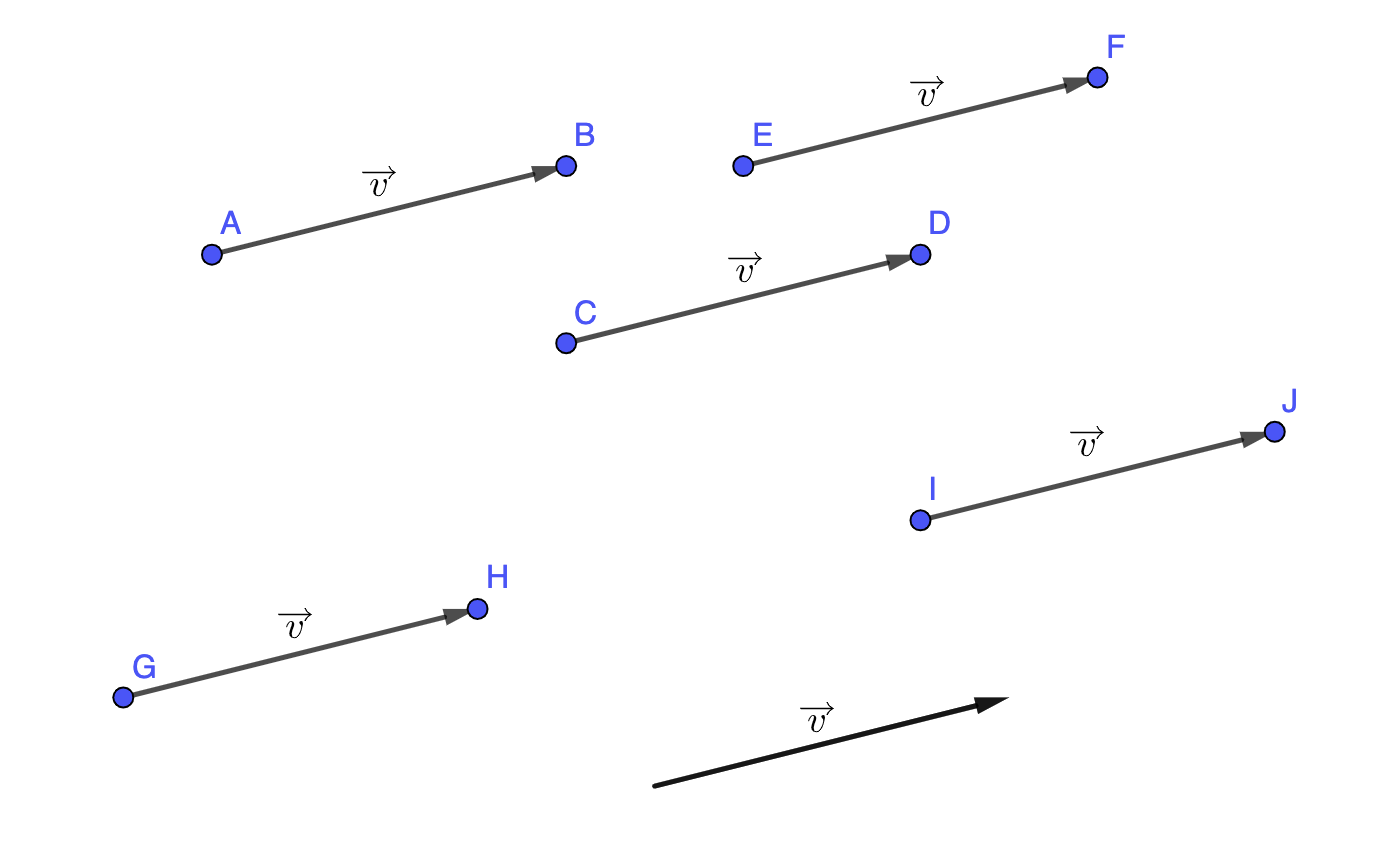
C'est aussi la raison pour laquelle nous n'utilisons qu'une seule lettre pour nommer le vecteur.
III) La somme de deux vecteurs
Pour effectuer la somme de deux vecteurs, il est nécessaires de connaitre les définitions et propriétés suivantes :
1) L'opposé d'un vecteur
On définit l'opposé d'un vecteur par :
Définition : L'opposé d'un vecteur \(\displaystyle \overrightarrow{v}\) du plan est le vecteur noté \(\displaystyle -\overrightarrow{v}\) tel que \(\displaystyle \overrightarrow{v}+\left(-\overrightarrow{v}\right)=\overrightarrow{0}\). Ainsi, un vecteur non nul et son opposé ont la même direction, la même norme, mais ont des sens contraires.
L'opposé du vecteur \(\displaystyle \overrightarrow{AB}\) se note \(\displaystyle -\overrightarrow{AB}\) mais peut s'écrire aussi \(\displaystyle \overrightarrow{BA}\).
2) La somme de deux vecteurs
On définit la somme de deux vecteurs de la façon suivante :
Définition : La somme de deux vecteurs \(\displaystyle \color{blue}{\overrightarrow{u}}\) et \(\displaystyle \color{orange}{\overrightarrow{v}}\) est le vecteur \(\displaystyle \color{red}{\overrightarrow{w}}\) associé à la translation qui résulte de l'enchainement des translations de vecteurs \(\displaystyle \color{blue}{\overrightarrow{u}}\) et de vecteur \(\displaystyle \color{orange}{\overrightarrow{v}}\). On écrira alors \(\displaystyle \color{blue}{\overrightarrow{u}}+\color{orange}{\overrightarrow{v}}=\color{red}{\overrightarrow{w}}\).
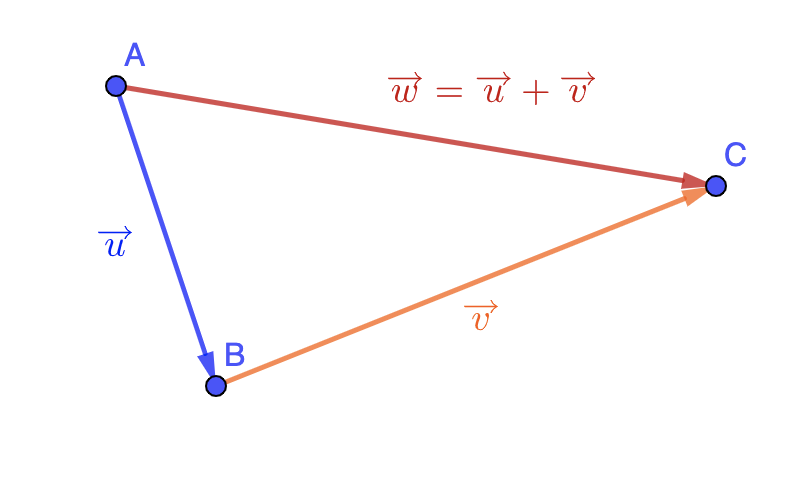
Propriété : On considère deux vecteurs \(\displaystyle \overrightarrow{u}\) et \(\displaystyle \overrightarrow{v}\) et trois points \(\displaystyle A\) , \(\displaystyle B\) et \(\displaystyle C\) tels que \(\displaystyle \overrightarrow{u}=\overrightarrow{AB}\) et \(\displaystyle \overrightarrow{v}=\overrightarrow{BC}\). On a alors \(\displaystyle \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\). Cette égalité s'appelle la relation de Chasles.
Exemple : En prenant trois points \(\displaystyle E\) , \(\displaystyle F\) et \(\displaystyle G\), on a \(\displaystyle \overrightarrow{EF}+\overrightarrow{FG}=\overrightarrow{EG}\).
Propriété : Pour tous vecteurs \(\displaystyle \overrightarrow{u}\) , \(\displaystyle \overrightarrow{v}\) et \(\displaystyle \overrightarrow{w}\), on a \(\displaystyle \overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u}\) ; \(\displaystyle \overrightarrow{u}+\overrightarrow{0}=\overrightarrow{u}\) et \(\displaystyle \overrightarrow{u}+\left(\overrightarrow{v}+\overrightarrow{w}\right)=\left(\overrightarrow{u}+\overrightarrow{v}\right)+\overrightarrow{w}\).
IV) Le produit d'un vecteur par un nombre réel
La multiplication existe avec des vecteurs. Au lycée, nous verrons le produit d'un vecteur par un nombre réel (en classe de 2nde), puis deux produits d'un vecteur par un vecteur : le produit scalaire et le produit vectoriel que nous verrons en 1ère et Tle.
1) Définition et proriété
Le produit d'un vecteur par un nombre se définit par la définition suivante :
Définition : On considère un vecteur \(\displaystyle \overrightarrow{AB}\) non nul du plan et un réel \(\displaystyle k\) non nul. Le produit \(\displaystyle k\overrightarrow{AB}\) est le vecteur qui a la même direction que \(\displaystyle \overrightarrow{AB}\), le même sens que \(\displaystyle \overrightarrow{u}\) lorsque \(\displaystyle k > 0\), un sens contraire lorsque \(\displaystyle k < 0 \) et pour norme \(\displaystyle \lvert k \rvert AB\). De plus, quelque soit le réel \(\displaystyle k\), \(\displaystyle k\overrightarrow{0}=\overrightarrow{0}\) et quelque soit le vecteur \(\displaystyle \overrightarrow{u}\), \(\displaystyle 0\overrightarrow{u}=\overrightarrow{0}\).
Exemple : En prenant l'exemple du milieu \(\displaystyle I\) d'un segment \(\displaystyle \left[AB\right]\), on a \(\displaystyle \overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}\).
Propriété : Pour tous vecteurs \(\displaystyle \overrightarrow{u}\) et \(\displaystyle \overrightarrow{v}\) et tous réels \(\displaystyle k\), on a : \(\displaystyle k\left(\overrightarrow{u}+\overrightarrow{v}\right)=k\overrightarrow{u}+k\overrightarrow{v}\). De même, on a \(\displaystyle k\left(\overrightarrow{u}-\overrightarrow{v}\right)=k\overrightarrow{u}-k\overrightarrow{v}\)
Propriété : Pour tous vecteurs \(\displaystyle \overrightarrow{u}\) et tous réels \(\displaystyle k\) et \(\displaystyle k'\), on a : \(\displaystyle \left(k+k'\right)\overrightarrow{u}=k\overrightarrow{u}+k'\overrightarrow{u}\). De même, on a \(\displaystyle \left(k-k'\right)\overrightarrow{u}=k\overrightarrow{u}-k'\overrightarrow{u}\)
Propriété : Pour tous vecteurs \(\displaystyle \overrightarrow{u}\) et tous réels \(\displaystyle k\) et \(\displaystyle k'\), on a : \(\displaystyle k\overrightarrow{u}=\overrightarrow{0}\)si et seulement si \(\displaystyle k=0\) ou \(\displaystyle \overrightarrow{u}=\overrightarrow{0}\).
2) La notion de colinéarité
La colinéarité de deux vecteurs est définie de la façon suivante :
Définition :Deux vecteurs \(\displaystyle \overrightarrow{u}\) et \(\displaystyle \overrightarrow{v}\) non nuls sont colinéaires lorsqu'il existe un nombre réel \(\displaystyle k\) non nul tel que \(\displaystyle \overrightarrow{u}=k\overrightarrow{v}\). Les vecteurs \(\displaystyle \overrightarrow{u}\) et \(\displaystyle \overrightarrow{v}\) étant colinéaires, cela signifie qu'ils ont la même direction.
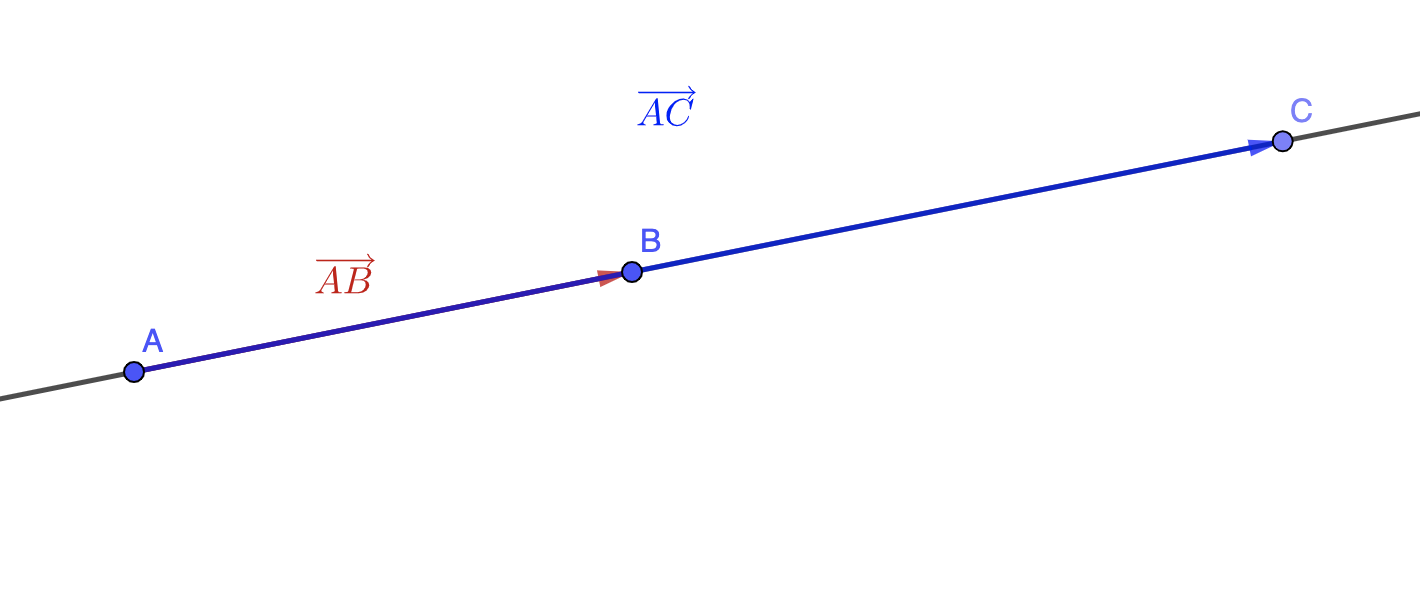
Propriété : Deux droites \(\displaystyle \left(AB\right)\) et \(\displaystyle \left(CD\right)\) sont parallèles si et seulement si les vecteurs \(\displaystyle \overrightarrow{AB}\) et \(\displaystyle \overrightarrow{CD}\) sont colinéaires.
Propriété : Trois points \(\displaystyle A\) , \(\displaystyle B\) et \(\displaystyle C\) sont alignés si et seulement si les vecteurs \(\displaystyle \overrightarrow{AB}\) et \(\displaystyle \overrightarrow{AC}\) sont colinéaires.