I) Mise en situation
Abordons la notion de fonction à l'aide d'un métier. Prenons celui d'enseignant. Le métier d'enseignant, comme beaucoup d'autres professions, sont pourvues de multi-fonctions, de multi-tâches. Une en particulier consiste à corriger une copie.
Pour ce faire, il procède en trois étapes :
- L'enseignant prend une copie au niveau de du tas de copies non corrigées.
- L'enseignant corrige, évalue et note la copie.
- L'enseignant la pose sur le tas de copies corrigées.
La situation peut être représentée de la façon suivante :
Ce schéma en trois parties peut se calquer sur plusieurs autres situations professionnelles. De manière générale, on retient la représentation suivante :
Il est possible aussi de le calquer sur des opérations mathématiques :
On imagine un ensemble de départ que l'on note \(\displaystyle D\) dans lequel se trouvent des nombres réels. On imagine un enchainement d'opérations qui consistera à prendre un nombre dans cet ensemble de départ, d'effectuer le calcul et de déposer ensuite le résultat dans un ensemble d'arrivé. On retrouve ici le schéma en trois étapes :
Il va falloir désormais utiliser un vocabulaire adéquat pour étudier une fonction en mathématiques.
II) Définitions
La fonction se définit de la façon suivante :
Définition : Soit \(\displaystyle D\) est intervalle ou une réunion d'intervalle de \(\displaystyle \mathbb{R}\). Une fonction notée \( \displaystyle f\) à valeurs réelles est un procédé qui associe à tout réel de \(\displaystyle D\), un unique réel noté \(\displaystyle f\left(x\right)\).
Exemple : Cette fonction traduit une relation de dépendance entre la variable de départ \(\displaystyle x\) et son résultat. On dit que \(\displaystyle f\left(x\right)\) est un résultat donné en fonction de \(\displaystyle x\).
Définition : L'ensemble de départ, \( \displaystyle D\) est appelé l'ensemble de définition de la fonction \( \displaystyle f\). Il est souvent noté aussi \(\displaystyle D_f\)
Définition : Les éléments \( \displaystyle x\) de \( \displaystyle D\) sont appelés les antécédents et le résultat \( \displaystyle f\left(x\right)\) est appelé l'image.
La notation de la fonction est : \(\displaystyle f:x\longmapsto f\left(x\right)\).
Exemple : La fonction \(\displaystyle f\) qui à chaque réel de \(\displaystyle D_f\) associe la fonction \(\displaystyle 3x+1\) s'écrit \(\displaystyle f:x\longmapsto 3x+1\).
Si on prend par exemple le nombre \(\displaystyle x=7\), alors il a pour image par la fonction \(\displaystyle f\), le nombre \(\displaystyle f\left(7\right)\). Par le calcul, on obtient \(\displaystyle f\left(7\right)=3\times7+1\), c'est-à-dire \(\displaystyle f\left(7\right)=22\).
7 est appelé l'image de 3 par la fonction \(\displaystyle f\) et 3 est appelé l'antécédent de 7 par la fonction \(\displaystyle f\).
III) Représentation graphique d'une fonction
La représentation graphique d'une fonction \(\displaystyle f\) se définit de la façon suivante :
Définition : Dans un repère du plan, on appelle courbe représentative ou représentation graphique de la fonction \(\displaystyle f\), notée \(\displaystyle C_f\), l'ensemble des points \(\displaystyle M\) de coordonnées \(\displaystyle (x;y)\) tels que \(\displaystyle x\in D_f\) et \(\displaystyle y=f\left(x\right)\).
La courbe \(\displaystyle C_f\) est ainsi formée de tous les points dont l'ordonnée est l'image \(\displaystyle y\) de l'abscisse \(\displaystyle x\) par la fonction \(\displaystyle f\).
Exemple : La courbe représentative de la fonction \(\displaystyle f\) définie par \(\displaystyle f\left(x\right)=x^2-1\) donne :
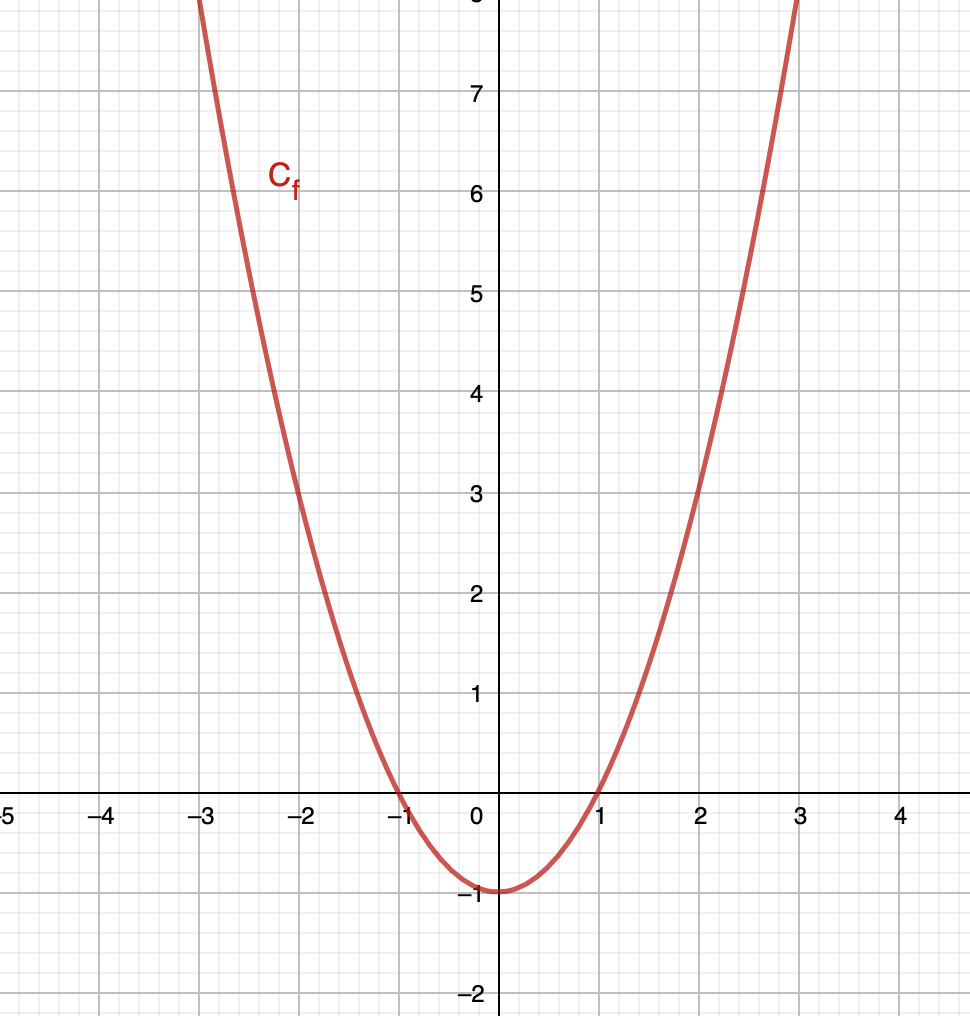
Il est ainsi possible de lire l'antécédent à partir d'une image, et une image à partir d'un antécédent.
IV) Variations d'une fonction
A partir d'une fonction, il est possible d'étudier ses variations ; c'est-à-dire connaître les valeurs de \(\displaystyle x\) pour lesquelles les valeurs de \(\displaystyle f\left(x\right)\) évoluent. On retient alors les définitions suivantes :
Définition : Soit deux nombres \(\displaystyle a\) et \(\displaystyle b\) d'un intervalle \(\displaystyle I\) tels que \(\displaystyle a < b \). Si \(\displaystyle f\left(a\right) < f\left(b\right)\) alors La fonction \(\displaystyle f\) est strictement croissante sur l'intervalle \(\displaystyle I\).
Exemple : La courbe représentative suivante montre une fonction croissante : quand \(\displaystyle x\) augmente, \(\displaystyle f\left(x\right)\) augemnte aussi :
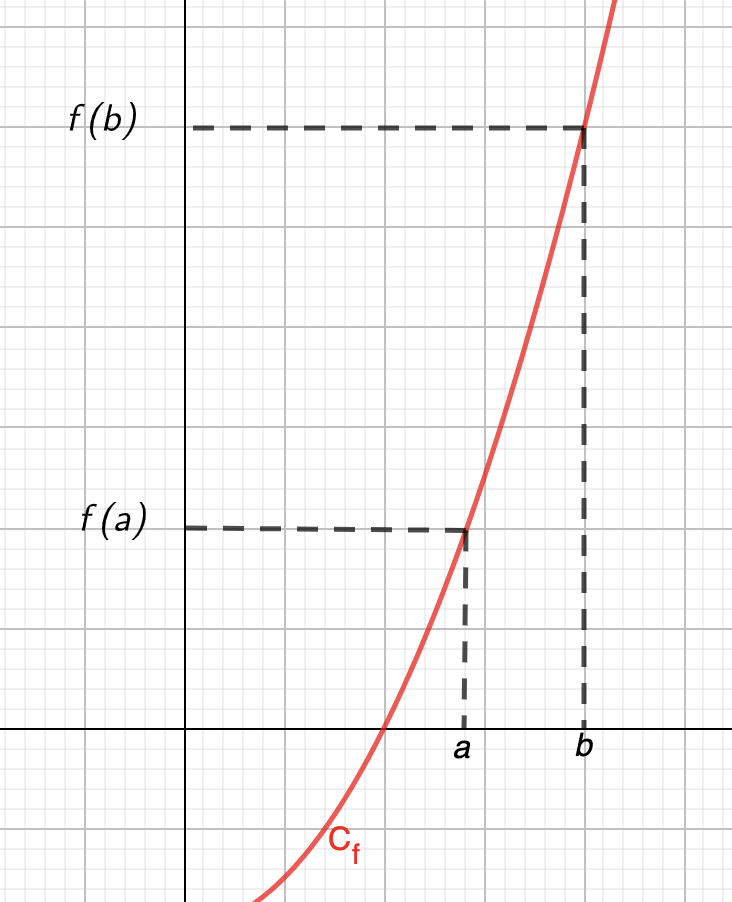
Définition : Soit deux nombres \(\displaystyle a\) et \(\displaystyle b\) d'un intervalle \(\displaystyle I\) tels que \(\displaystyle a < b \). Si \(\displaystyle f\left(a\right) > f\left(b\right)\) alors La fonction \(\displaystyle f\) est strictement décroissante sur l'intervalle \(\displaystyle I\).
Exemple : La courbe représentative suivante montre une fonction décroissante : quand \(\displaystyle x\) augmente, \(\displaystyle f\left(x\right)\) diminue :
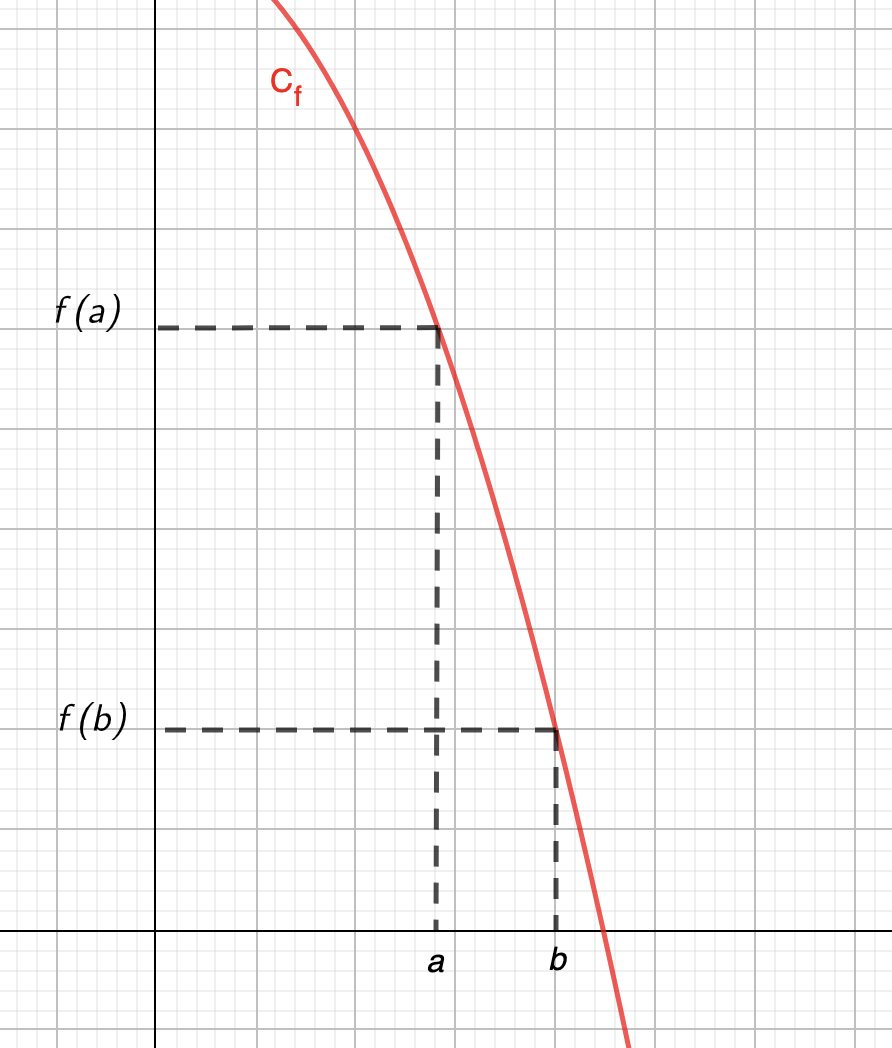
Définition : Lorsque sur un intervalle \(\displaystyle I\), la fonction est soit strictement croissante sur \(\displaystyle I\) ou soit strictement décroissante sur \(\displaystyle I\), la fonction est strictement monotone.
Définition : Soit deux nombres \(\displaystyle a\) et \(\displaystyle b\) d'un intervalle \(\displaystyle I\) tels que \(\displaystyle a < b \). Si \(\displaystyle f\left(a\right) = f\left(b\right)\) alors La fonction \(\displaystyle f\) est constante sur l'intervalle \(\displaystyle I\).
Exemple : La courbe représentative suivante montre une fonction constante : quand \(\displaystyle x\) augmente, \(\displaystyle f\left(x\right)\) n'évolue pas :
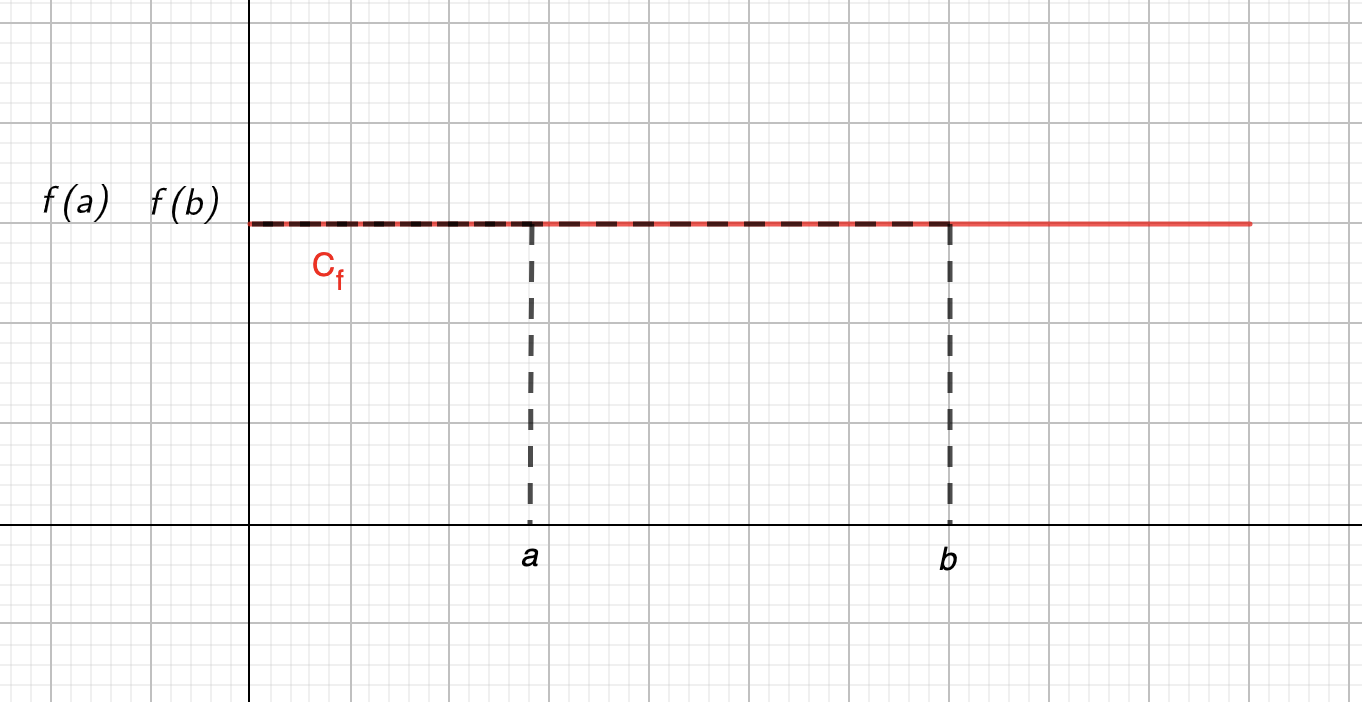
Les variations d'une fonction peuvent être résumées dans un tableau de variation. Celui-ci est composé de deux lignes. En réalité, il est composé de trois lignes mais cette troisième ligne ne sera étudiée qu'à partir de la classe de 1ère. C'est la raison pour laquelle il n'est précisé en classe de 2nde que deux lignes.
La première ligne concerne les valeurs de \(\displaystyle x\). Si la fonction \(\displaystyle f\) est étudiée sur l'intervalle \(\displaystyle I=\left[a;b\right]\), alors la première ligne fera état des valeurs comprises entre \(\displaystyle a\) et \(\displaystyle B\).
La deuxième ligne indique les variations de la fonction par des flèches montantes pour un état de croissance, et/ou par des flèches déscendantes pour un état de décroissance. Aux extrémités de ces flêches, sont indiquées les images qui correspondent aux valeurs de la première ligne.
Exemple : On propose dans un premier temps la courbe représéntative d'une fonction \(\displaystyle f\) définie sur un intervalle \(\displaystyle I=\left[1;9\right]\) :
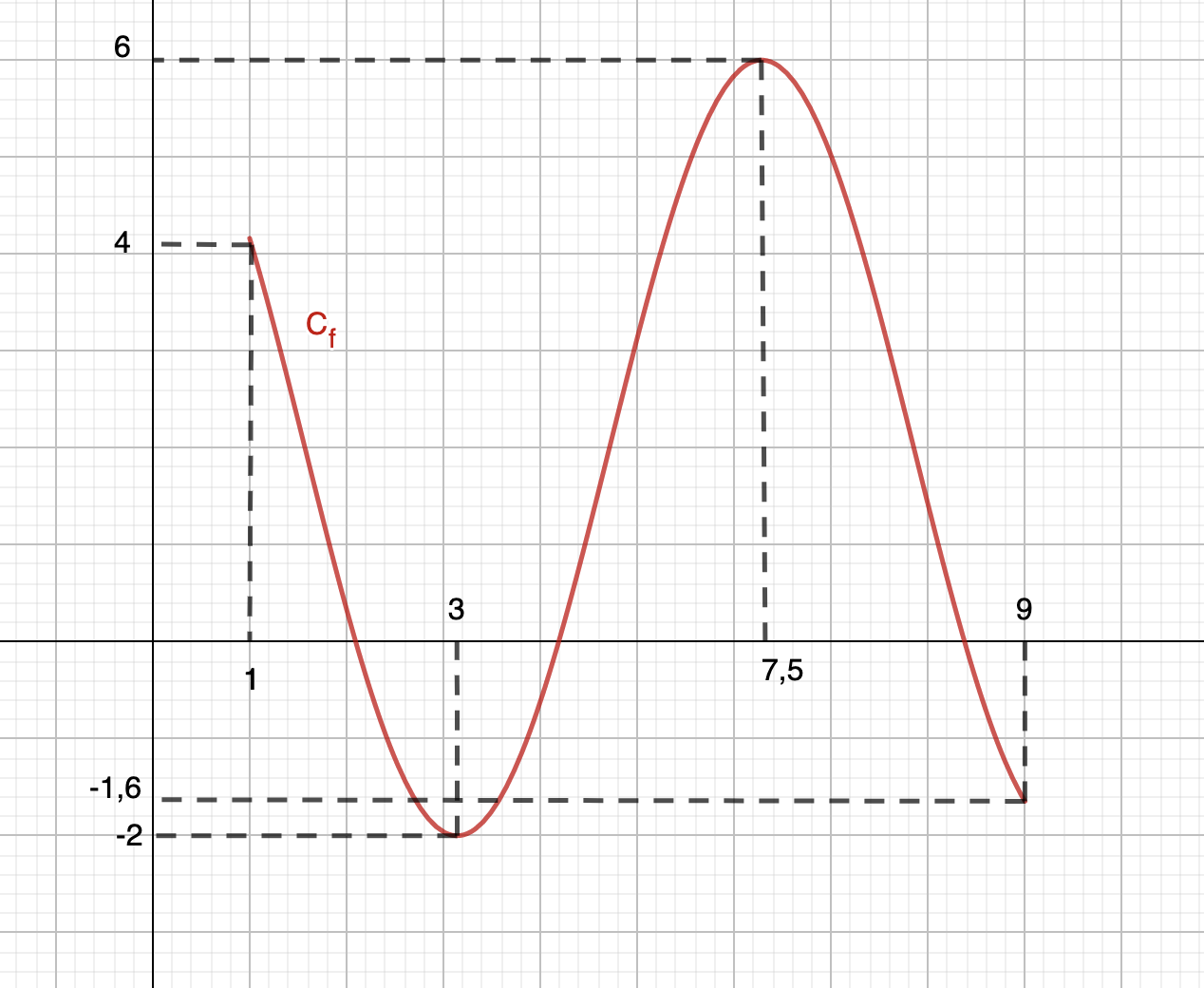
Son tableau de variation donne :
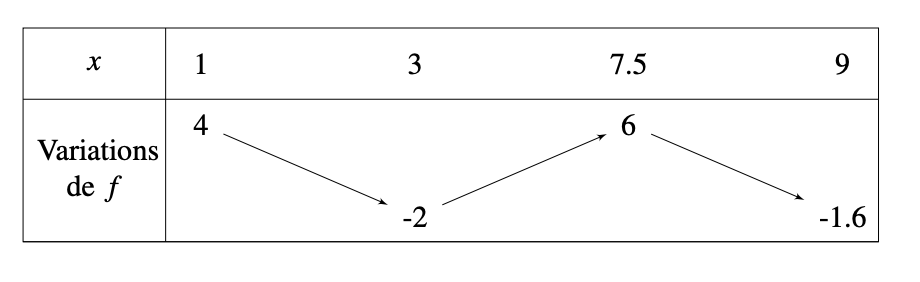
V) Notion d'extremum
On définit un ou plusieurs extremums d'une fonction de la façon suivante :
Définition : Rechercher les extremums de la fonction \(\displaystyle f\) sur un intervalle \(\displaystyle I\), c'est déterminer le minimum et le maximum de \(\displaystyle f\) sur \(\displaystyle I\) (lorsqu'ils existent).
Définition : Le minimum, noté \(\displaystyle m\) de la fonction \(\displaystyle f\) sur l'intervalle \(\displaystyle I\) (lorsqu'il existe) est égal à la plus petite image possible par \(\displaystyle f\) pour un nombre appartenant à \(\displaystyle I\). DAns ce cas, pour tout nombre \(\displaystyle x\) de \(\displaystyle I\), on a \(\displaystyle f\left(x\right) \geqslant m\).
Définition : Le maximum, noté \(\displaystyle M\) de la fonction \(\displaystyle f\) sur l'intervalle \(\displaystyle I\) (lorsqu'il existe) est égal à la plus grande image possible par \(\displaystyle f\) pour un nombre appartenant à \(\displaystyle I\). DAns ce cas, pour tout nombre \(\displaystyle x\) de \(\displaystyle I\), on a \(\displaystyle f\left(x\right) \leqslant M\).
Exemple : Dans l'exemple du paragraphe précédent, sur l'intervalle \(\displaystyle I=\left[1;9\right]\), le minimum est atteint à \(\displaystyle m=-2\) pour \(\displaystyle x=3\). Le maximum est atteint à \(\displaystyle M=6\) pour \(\displaystyle x=7,5\).
VI) Parité d'une fonction
On définit la parité d'une fonction de la façon suivante :
Définition : On considère une fonction \(\displaystyle f\) définie sur \(\displaystyle D_f\). On dit que \(\displaystyle f\) est paire si \(\displaystyle D_f\) est centré en 0 et si pour tout réel \(\displaystyle x\) de \(\displaystyle D_f\), on a \(\displaystyle f\left(-x\right)=f\left(x\right)\).
Définition : On considère une fonction \(\displaystyle f\) définie sur \(\displaystyle D_f\). On dit que \(\displaystyle f\) est impaire si \(\displaystyle D_f\) est centré en 0 et si pour tout réel \(\displaystyle x\) de \(\displaystyle D_f\), on a \(\displaystyle f\left(-x\right)=-f\left(x\right)\).
Exemple graphique d'une fonction paire : La courbe \(\displaystyle \left(C_f\right)\) est symétrique par rapport à l'axe des ordonnées :
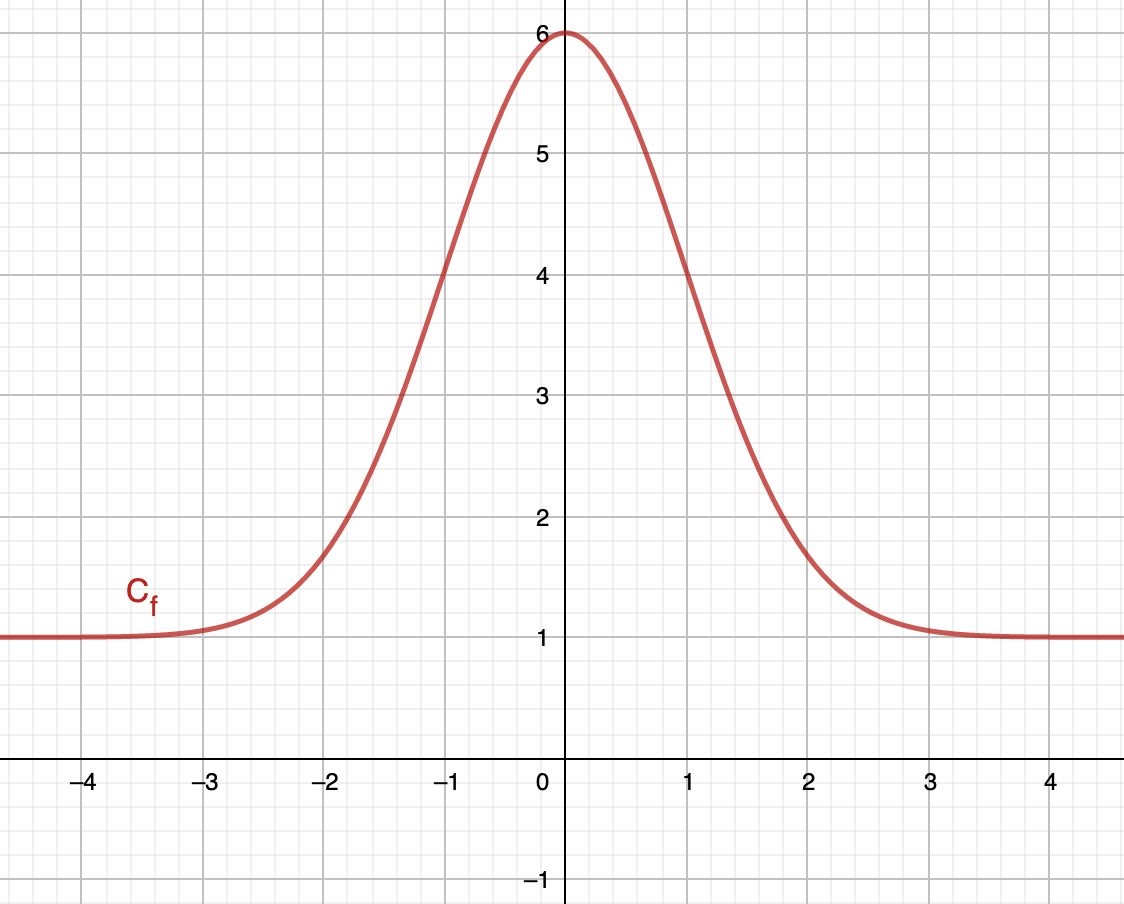
Exemple graphique d'une fonction impaire : La courbe \(\displaystyle \left(C_f\right)\) est symétrique par rapport à l'origine du repère :