I) Mise en situation
L'Egypte est un pays d'Afrique connu pour son histoire et les edifices magnifiques qui y ont été construits il y a -2500 ans comme par exemple les pyramides. Dans la région de Gizeh, on en compte 3 célèbres : la pyramide de Mykérinos, celle de Képhren et la plus connue : celle de Khéops.
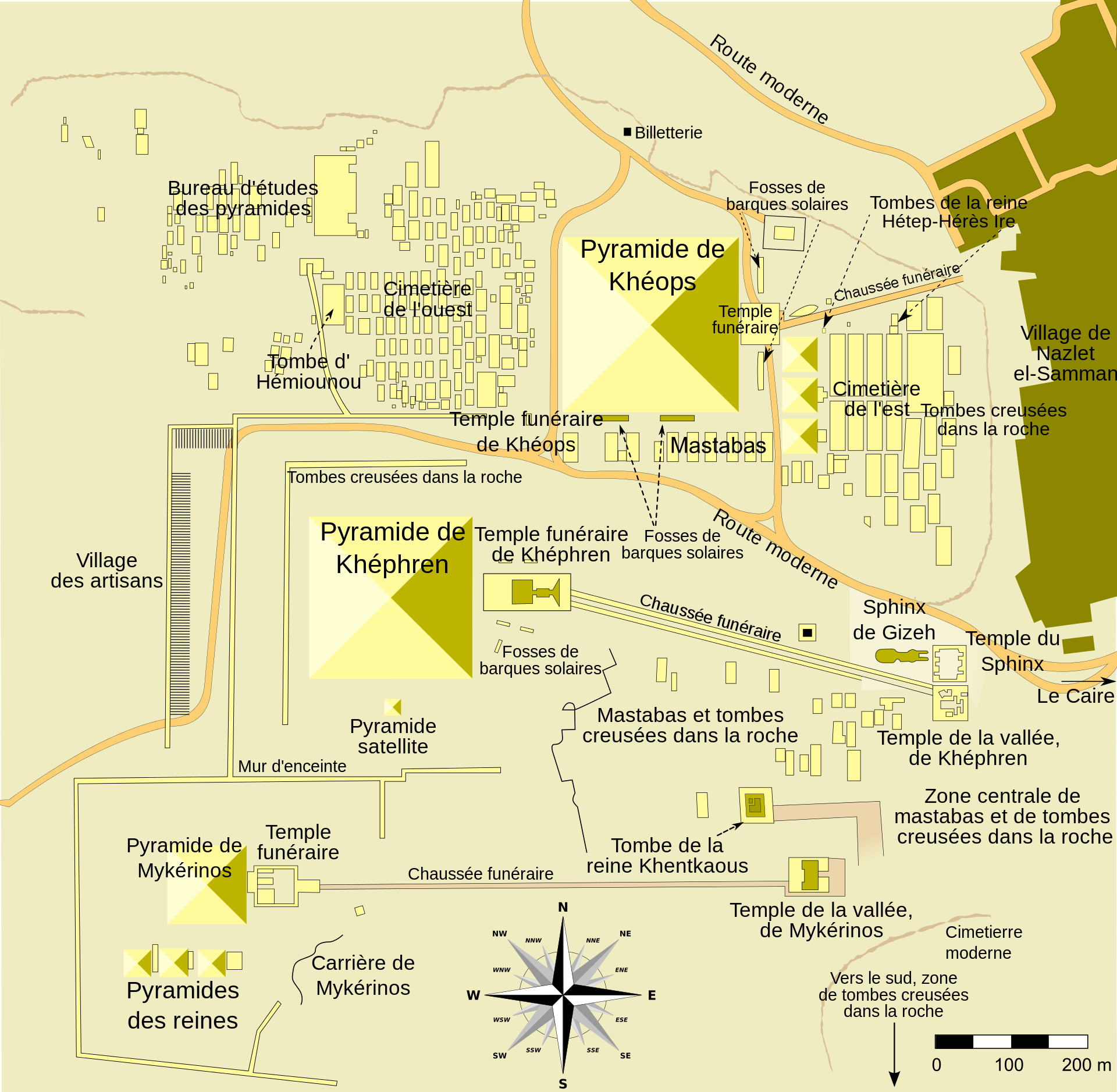
Cette dernière possède une hauteur \(\displaystyle h=148,2\)m et un côté \(\displaystyle c=232,8\)m de sa base carrée.
Pour calculer la longueur de son apothème, nous nous plaçons dans la situation suivante en utilisant le théorème de Pythagore :
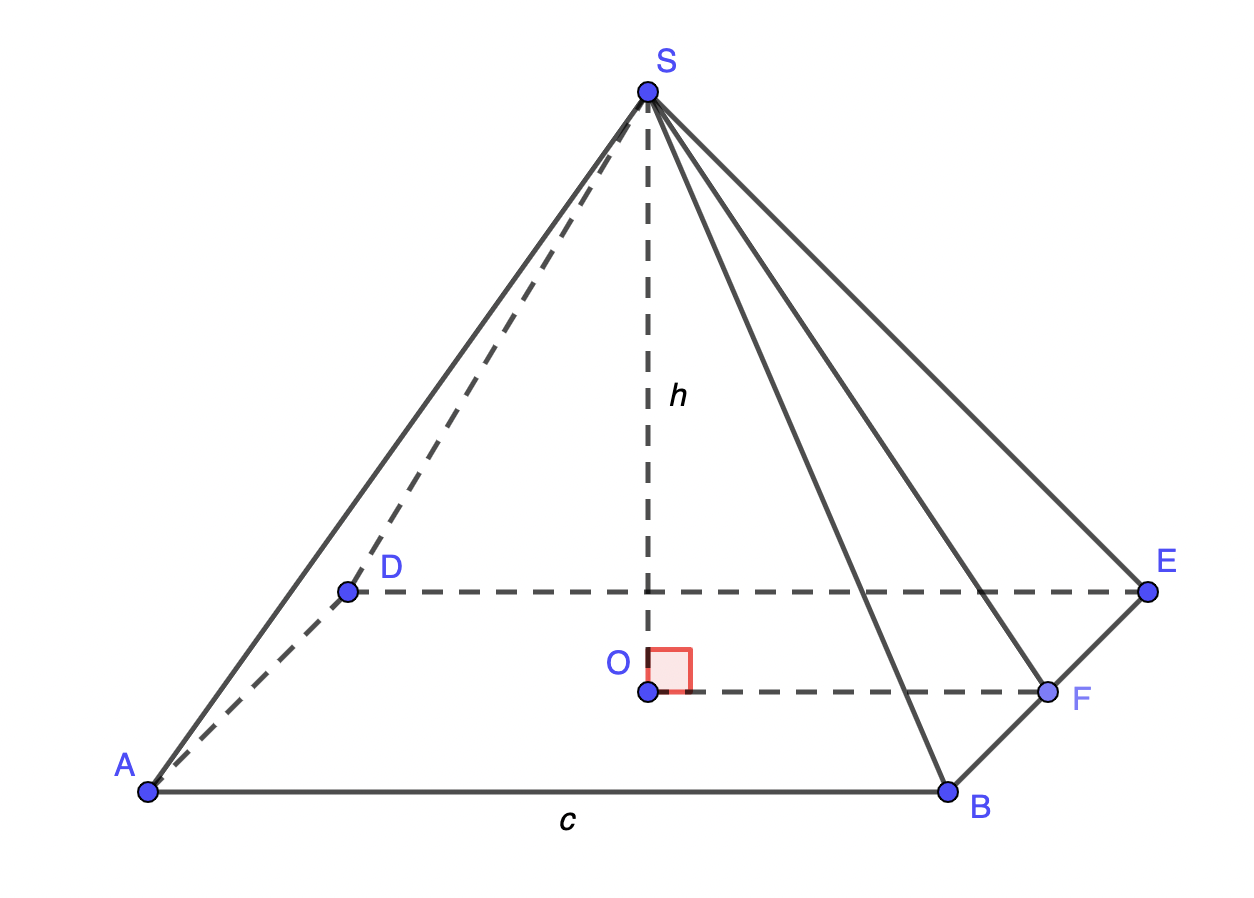
Sur la figure, l'apothème est représentée par le segment \(\displaystyle \left[SF\right]\).
On souhaite ici calculer le rapport qui existe entre la longueur de cette apothème et celle de la base, par l'activité suivante : activité n°1.
Pour calculer sa longueur, nous nous plaçons dans le triangle rectangle \(\displaystyle SOF\) rectangle en \(\displaystyle O\). Nous pouvons ainsi utiliser le théorème de Pythagore en écrivant la relation \(\displaystyle SF^2=OF^2+OS^2\). Elle peut s'écrire aussi \(\displaystyle SF^2=h^2+\left(\frac{c}{2}\right)^2\) et on obtient \(\displaystyle SF=\sqrt{h^2+\left(\frac{c}{2}\right)^2}\).
Avec les valeurs de \(\displaystyle h\) et de \(\displaystyle c\), à l'aide de la calculatrice, on arrive au résultat \(\displaystyle SF\simeq188,44\)m.
Une fois ce résultat obtenu, amusons-nous à créer le rapport de cette apothème par la moitié du côté de la base, à savoir le rapport \( \displaystyle \frac{SF}{OF}\). Nous obtenons la valeur 1,61803.... (un nombre très particulier que nous retrouverons très prochainement)
Je réalise ce petit exercice sur la pyramide pour montrer que j'ai utilisé différents nombres. J'ai utilisé en effet le nombre 3 ; le nombre -2500 ; le nombre 148,2 ; le nombre 232,8 ; une fraction et enfin le nombre 1,61803...
Ces nombres se classent dans différents ensembles :
• Depuis les classes de maternelle jusqu'à aujourd'hui, nons utilisons les nombres pour compter. Il s'agit des nombres 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; 10 ; 11 ; 12 ; etc. Nous les utilisons nautrellement dans la vie quotidienne. Ce sont des entiers naturels et font parties de l'ensemble des entiers naturels que l'on note \(\displaystyle \mathbb{N}\).
• Il nous est arrivé aussi de placer un signe + ou un signe - devant les nombres entiers. Il s'agit ici des nombres entiers relatifs. Ils font partie de l'ensemble des entiers relatifs que l'on note \(\displaystyle \mathbb{Z}\).
• N'oublions pas aussi les nombres décimaux relatifs : ces nombres avec une virgule et une quantité finie de chiffres derrière la virgule. Ils font partie de l'ensemble des décimaux relatifs que l'on note \(\displaystyle \mathbb{D}\).
• Il existe des nombres à virgule avec une quantité de chiffres infinie derrière la virgule. Parmi ces nombres, certains peuvent s'écrire sous forme d'une fraction représentant une ration. Ils sont appelés les rationnels. Ils font partie de l'ensemble des rationnels que l'on note \(\displaystyle \mathbb{Q}\).
• Ensuite, parmi ces nombres qui ne peuvent pas s'écrire sous forme de fraction, quelques-uns peuvent s'écrire à l'aide d'une formule et d'autres non. Ceux qui ne peuvent pas s'écrire sous forme d'une formule sont appelés les nombres transcendants, comme par exemple le nombre \(\displaystyle \pi\). Ceux qui peuvent s'écrire sous forme d'une formule ne portent pas de nom et nous pouvons citer en exemple le nombre d'or. Il se note \( \displaystyle \phi\) et se définit par la formule \( \displaystyle \phi=\frac{1+\sqrt{5}}{2}\). Comment alors classer ces autres nombres à virgule qui ne peuvent pas s'écrire sous forme d'une fraction de nombres entiers ? Ils sont appelés les irrationnels. Ainsi, l'ensemble des rationnels et des irrationnels forment l'ensemble des réels que l'on note \(\displaystyle \mathbb{R}\).
Il existe d'autres ensembles de nombres comme les nombres complexes, les quaternions, etc. Ces ensembles seront vus en classe de terminale ou dans les niveaux d'études post-bac.
II) L'ensemble des réels \(\displaystyle \mathbb{R}\)
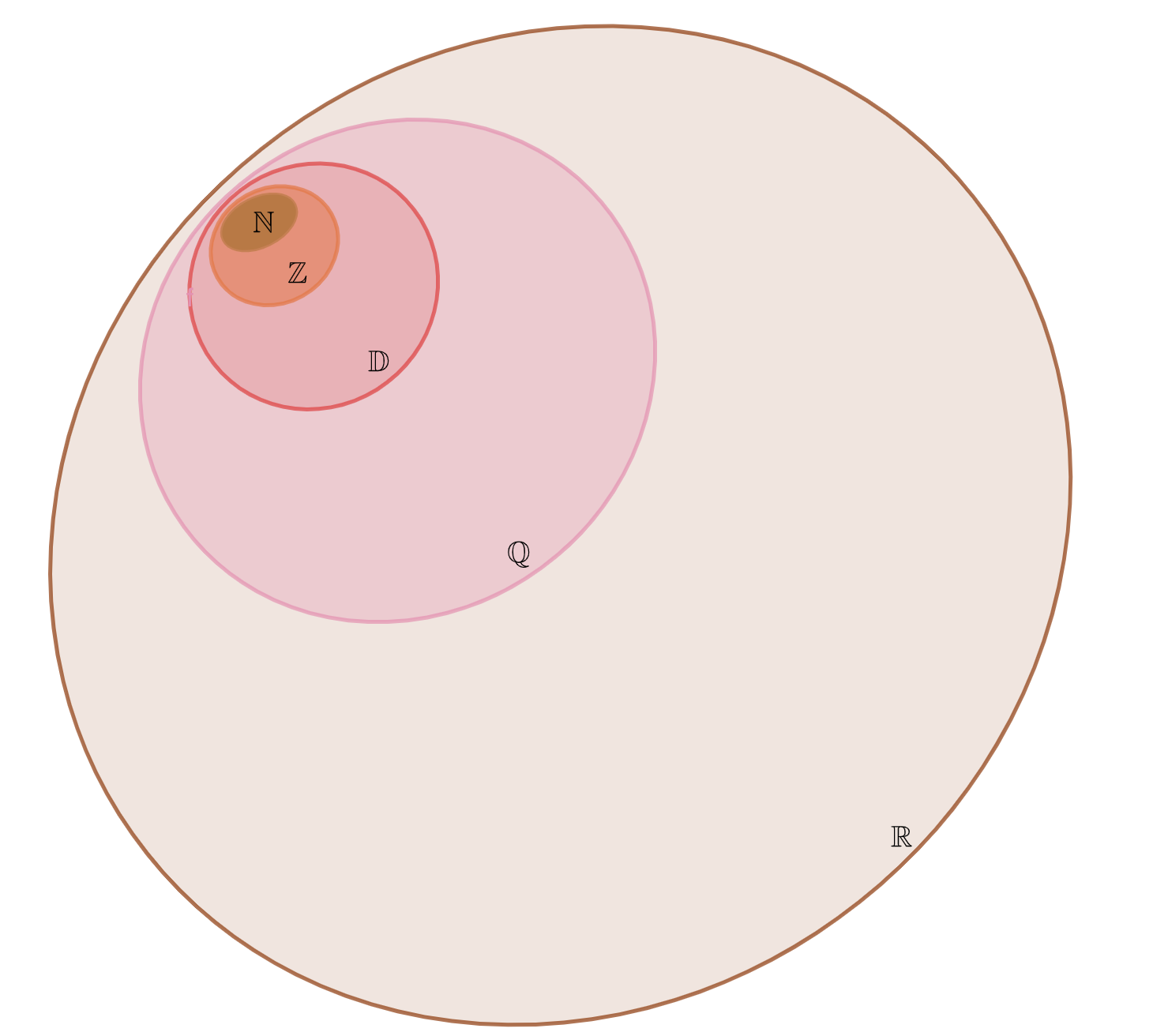
Nous pouvons remarquer que les nombres réels incluent tous les nombres que nous avons rencontrés depuis que nous sommes à l'école. Ainsi, nous pouvons écrire une relation du type \(\displaystyle \mathbb{N}\subset\mathbb{Z}\subset\mathbb{D}\subset\mathbb{Q}\subset\mathbb{R}\). Cet enchainement d'inclusion se shématise de la façon suivante :
1) La droite des réels
Généralement, l'ensemble des réels est représenté par une droite graduée sur laquelle sont représentés des points et leur abscisse respectif. Elle est appelée la droite des réels. A chaque point de cette droit est associé un unique rée représentant son abscisse. Ainsi, à chaque réel est associé un unique point de cette droite.
2) La notion d'intervalle
Nous définissons un intervalle de la façon suivante :
Définition : Soient \( \displaystyle a\) et \( \displaystyle b\) deux nombres réels tels que \( \displaystyle a < b\). L'intervalle \( \displaystyle \left[a;b\right] \) est l'ensemble des réels tels que \( \displaystyle a\leqslant x \leqslant b\).
Sur la droite des réels, cet intervalle est représenté de la façon suivante :

Nous définissons aussi un intervalle de la façon suivante :
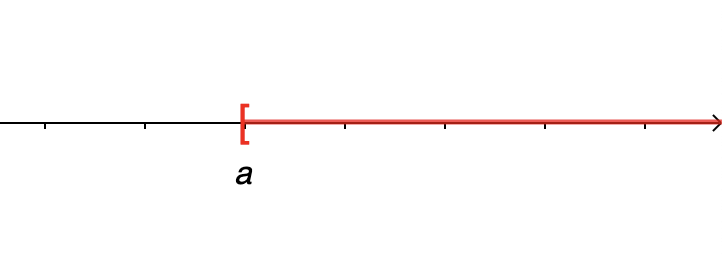
Définition : L'intervalle \( \displaystyle \left[a;+\infty\right[ \) est l'ensemble des réels tels que \( \displaystyle x \geqslant a\).
Sur la droite des réels, cet intervalle est représenté de la façon suivante :
Le sens du crochet dans l'écriture de l'intervalle est important. Nous distinguerons le crochet ouvert pour exclure la borne de l'intervalle et le crochet fermé pour inclure la borne de l'intervalle. Par exemple, dans l'ecriture \( \displaystyle \left[a;b\right[\), le crochet est fermé pour la borne \( \displaystyle a\) : le réel \( \displaystyle a\) est inclu dans l'intervalle. En revanche, le crochet est ouvert pour la borne \( \displaystyle b\) : le réel \( \displaystyle b\) est exclu de l'intervalle.
Il est possible de manipuler les intervalles ont les unissant de deux façons suivantes :
Définition : L'intersection de deux intervalles \( \displaystyle I\) et \( \displaystyle J\) est notée \( \displaystyle I\cap J\) et se définie par l'ensemble des réels \( \displaystyle x\) appartenant à \( \displaystyle I\) et à \( \displaystyle J\). Le symbole \( \displaystyle \cap\) se lit « inter ».
Exemple : Dans le schéma suivant, si \( \displaystyle I=\left[-3;3\right]\) et \( \displaystyle J=\left[0;7\right]\) alors \( \displaystyle I\cap J=\left[1;6\right]\).

Définition : L'union de deux intervalles \( \displaystyle I\) et \( \displaystyle J\) est notée \( \displaystyle I\cup J\) et se définie par l'ensemble des réels \( \displaystyle x\) appartenant à \( \displaystyle I\) ou à \( \displaystyle J\). Le symbole \( \displaystyle \cup\) se lit « union ».
Exemple : Dans le schéma suivant, si \( \displaystyle I=\left[-3;3\right]\) et \( \displaystyle J=\left[0;7\right]\) alors \( \displaystyle I\cup J=\left[-3;7\right]\).

Remarque : Qu'entendons-nous par « ou » ? En mathématiques, le « ou » n'est pas inclusif. Cela signifie que nous incluons la possibilité du « et ». Autrement dit, lorsqu'un nombre réel \( \displaystyle x\) appartient à \( \displaystyle I\cup J\), cela signifie qu'il appartient à \( \displaystyle I\) ou à \( \displaystyle J\), mais que l'appartenance aux deux ensembles à la fois est aussi possible.
3) La notion de valeur absolue
Considérons ici deux points \( \displaystyle A\) et \( \displaystyle B\) placé sur la droite des réels donc les absicesses respectives sont \( \displaystyle a\) et \( \displaystyle b\). Si la distance mesurée entre les points \( \displaystyle A\) et \( \displaystyle B\) s'écrit \( \displaystyle AB\), elle peut aussi s'écrire à l'aide des abscisses \( \displaystyle a\) et \( \displaystyle b\) à l'aide de la notion de valeur absolue, définie de la façon suivante :
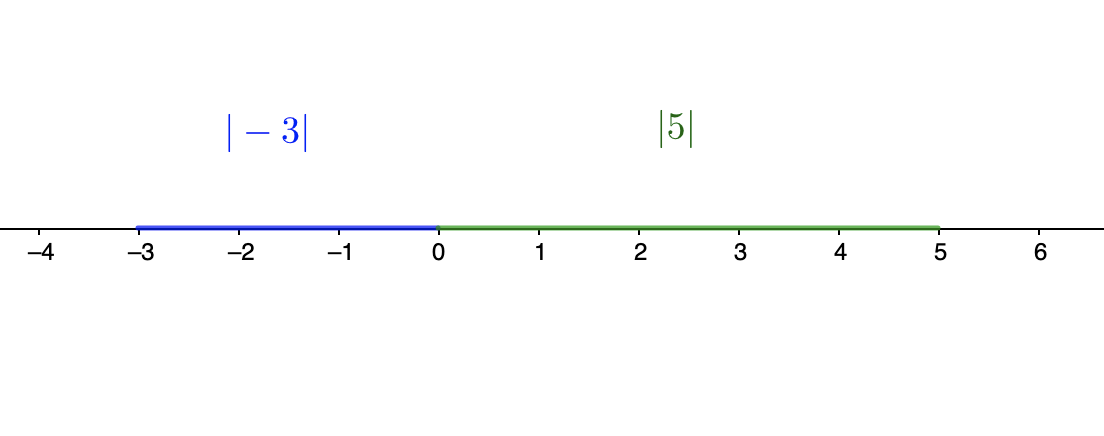
Définition : Soit un point \( \displaystyle M\) d'abcisses \( \displaystyle x\) placé sur la droite des réels. La valeur absolue de \( \displaystyle x\), notée \( \displaystyle \lvert x \rvert\) est égale à la distance \( \displaystyle OM\).
Exemple : Dans le schéma suivant, nous pouvons écrire \( \displaystyle \lvert -3 \rvert =3\) et \( \displaystyle \lvert 5 \rvert=5\)
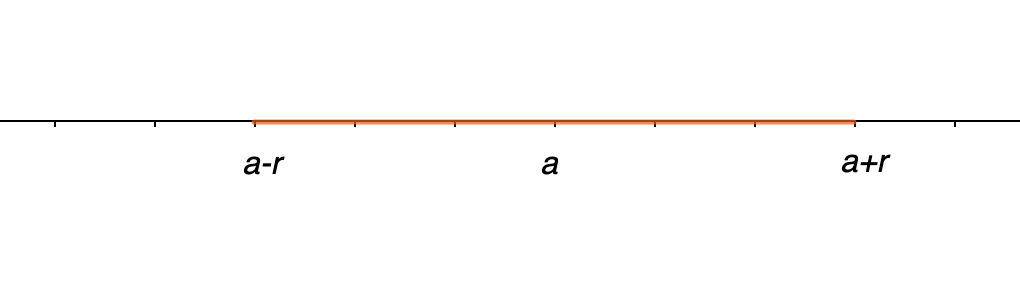
Nous serons souvent amenés à utiliser des intervalles construits à partir d'une valeur réelle de départ notée \( \displaystyle a\). L'intervalle est ensuite construit avec une autre valeur réelle notée \( \displaystyle r\) telles que l'intervalle s'écrive \( \displaystyle \left[a-r;a+r\right]\). Ainsi, les valeurs de \( \displaystyle x\) vérifient l'inégalité \( \displaystyle a-r\leqslant x \leqslant a+r\). Avec la notion de valeur absolue, nous pouvons alors écrire \( \displaystyle \lvert x-a \rvert \leqslant r\). Le principe est schématisé de la façon suivante :
III) L'ensemble des décimaux \(\displaystyle \mathbb{D}\)
Les nombres décimaux sont définis de la façon suivante :
Définition : Un nomnbre \(\displaystyle d\) est un nombre décimal s'il existe un entier relatif \(\displaystyle a\) et un entier naturel \(\displaystyle n\) tel que \(\displaystyle d=\frac{a}{10^n}\).
A partir de cette définition, nous pouvons écrire deux propriétés suivantes :
Propriété (admise) : Un nombre décimal admet une partie décimale qui peut s'écrire avec une quantité finie de chiffres.
Propriété (admise) : Pour tout réel \(\displaystyle x\) et tout entier naturel \(\displaystyle n\), il existe un nombre décimal \(\displaystyle d\) tle que \(\displaystyle \lvert x-d \rvert\leqslant \frac{1}{10^n}\). Le nombre \(\displaystyle d\) est alors appelé valeur approchée de \(\displaystyle x\) à \(\displaystyle 10^{-n}\) près.
Remarque : Les nombres écrits sous forme de fraction, sont-ils tous des décimaux ? Quand est-il du nombre \(\displaystyle \frac{1}{3}\) ?
Démonstration à savoir : Démontrons que \(\displaystyle\frac{1}{3}\) n'est pas un nombre décimal :
Pour cela, on raisonne par l'absurde en supposant que \(\displaystyle\frac{1}{3}\) est un nombre décimal. Dans ce cas, il existe un entier relatif \(\displaystyle a\) et un entier naturel \(\displaystyle n\) tel que \(\displaystyle\frac{1}{3}=\frac{a}{10^n}\).
Alors, \(\displaystyle a=\frac{10^n}{3}\).
Or, une puissance de 10 n'est jamais divisible par 3. la fraction \(\displaystyle\frac{10^n}{3}\) n'est donc pas entière.
Ainsi, le nombre \(\displaystyle a\) ne peut pas être entier, ce qui contredit l'hypothèse. On en déduit que \(\displaystyle\frac{1}{3}\) n'est pas un nombre décimal.
IV) L'ensemble des rationnels \(\displaystyle \mathbb{Q}\)
Les nombres rationnels sont définis de la façon suivante :
Définition : Un nomnbre \(\displaystyle q\) est un nombre rationnel s'il existe deux entiers relatifs \(\displaystyle a\) et \(\displaystyle b\) avec \(\displaystyle b\neq0\), tels que \(\displaystyle q=\frac{a}{b}\).
Remarque : Les nombres réels, sont-ils tous des rationnels ? Quand est-il du nombre \(\displaystyle \sqrt{2}\) ?
Démonstration à savoir : Démontrons que \(\displaystyle\sqrt{2}\) n'est pas un nombre rationnel :
Pour cela, on raisonne par l'absurde en supposant que \(\displaystyle\sqrt{2}\) puisse s'écrire sous la forme \(\displaystyle\sqrt{2}=\frac{a}{b}\).
Alors \(\displaystyle\left(\sqrt{2}\right)^2=\left(\frac{a}{b}\right)^2\), soit \(\displaystyle\left(\frac{a}{b}\right)^2=2\) ou encore \(\displaystyle a^2=2b^2\).
Puisque ces nombres sont égaux, ils ont le même chiffre des unités. On en déduit que le chiffre des unités de \(\displaystyle a^2\) et de \(\displaystyle 2b^2\) soit égal à 0. (voir tableau ci-dessous).
Le chiffre des unités de \(\displaystyle a^2\) étant 0, celui de \(\displaystyle a\) est aussi 0 ce qui implique que \(\displaystyle a\) est un multiple de 10. Ensuite, le chiffre des unités de \(\displaystyle 2b^2\) étant 0, celui de \(\displaystyle b\) est 0 ou 5. Ce qui implique que \(\displaystyle b\) est un multiple de 5. Ainsi, la fraction \(\displaystyle \frac{a}{b}\) peut être simplifiée par 5 : elle n'est pas irréductible, ce qui contredit l'hypothèse de départ.
On en conclut que \(\displaystyle \sqrt{2}\) n'est pas rationnel.
| \(\displaystyle a\) | \(\displaystyle b\) | \(\displaystyle a^2\) | \(\displaystyle 2b^2\) |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 2 |
| 2 | 2 | 4 | 8 |
| 3 | 3 | 9 | 18 |
| 4 | 4 | 16 | 32 |
| 5 | 5 | 25 | 50 |
| 6 | 6 | 36 | 72 |
| 7 | 7 | 49 | 98 |
| 8 | 8 | 64 | 128 |
| 9 | 9 | 81 | 162 |
V) L'ensemble des entiers relatifs \(\displaystyle \mathbb{Z}\)
Revoyons ici quelques notions déjà apperçues au collège.
1) Les quatre opérations dans \(\displaystyle \mathbb{Z}\)
Rappelons ici que l'ensemble des entiers naturels est noté \(\displaystyle \mathbb{N}\) et que celui des entiers relatifs est noté \(\displaystyle \mathbb{Z}\).
La somme, la différence et la multiplication de deux nombres relatifs sont des entiers relatifs. Concernant la division, nous utilisons la division euclidienne : si pour deux entiers relatifs \(\displaystyle a\) et \(\displaystyle b\), avec \(\displaystyle b\) non nul, nous pouvons écrire \(\displaystyle a\) sous la forme \(\displaystyle a=bq+r\), où \(\displaystyle q\) est un entier relatif et \(\displaystyle r\), un entier naturel tel que \(\displaystyle 0\leqslant r < \lvert b \rvert q\). Le nombre \(\displaystyle q\) est appelé le quotient et le nomnbre \(\displaystyle r\) est appelé le reste de la division.
2) La notion de multiple dans \(\displaystyle \mathbb{Z}\)
Un multiple d'un nombre relatif se définit de la façon suivante :
Définition : On considère deux entiers relatifs \(\displaystyle n\) et \(\displaystyle p\). Si le reste de la division euclidienne de \(\displaystyle n\) par \(\displaystyle p\) est égal à 0, alors \(\displaystyle p\) est un diviseur de \(\displaystyle n\) et \(\displaystyle n\) est un multiple de \(\displaystyle p\).
Quand on dit que \(\displaystyle p\) est un diviseur de \(\displaystyle n\), on dit aussi que \(\displaystyle n\) est divisible par \(\displaystyle p\).
Aussi, tout nombre entier relatif non nul \(\displaystyle n\) admet une infinité de multiples qui s'écrivent sous la forme \(\displaystyle kn\) où \(\displaystyle k\) est un entier relatif.
Propriété (démontrée) : On considère trois entiers relatifs \(\displaystyle a\), \(\displaystyle n\) et \(\displaystyle m\). Si les entiers \(\displaystyle n\) et \(\displaystyle m\) sont deux multiples de \(\displaystyle a\), alors la somme \(\displaystyle n+m\) , la différence \(\displaystyle n-m\) et le produit \(\displaystyle nm\) sont aussi des multiples de \(\displaystyle a\).
Démonstration à savoir : Démontrons la propriété précédente pour la somme.
Comme \(\displaystyle n\) est un multiple de \(\displaystyle a\), on peut écrire \(\displaystyle a=k_1n\) où \(\displaystyle k_1\) est un entier relatif. De même, on peut écrire \(\displaystyle m=k_2a\) où \(\displaystyle k_2\) est aussi un entier relatif, car \(\displaystyle m\) est un multiple de \(\displaystyle a\).
On en déduit que \(\displaystyle n+m=k_1a+k_2a\) soit encore \(\displaystyle n+m=\left(k_1+k_2\right)a\).
Or, \(\displaystyle k_1+k_2\) est la somme de deux entiers relatifs, elle est donc aussi un entier relatif.
Ainsi, par définition, \(\displaystyle a\) est un diviseur de \(\displaystyle n+m\).
Autrement dit, la somme \(\displaystyle n+m\) est un multiple de \(\displaystyle a\).
V) L'ensemble des entiers naturels \(\displaystyle \mathbb{N}\)
Revoyons ici quelques notions déjà apperçues au collège.
1) La notion de nombre premier
Un nombre premier se définit de la façon suivante :
Définition : Un nombre entier naturel est dit premier s'il admet que deux diviseurs positifs distincts : 1 et lui-même.
Remarque : Le nombre 1 est-il un nombre premier ? Il n'est divisible que par 1 et lui-même, mais ces deux diviseurs ne sont pas distintcs. 1 n'est donc pas un nombre premier.
Les nombres premiers peuvent être considérés comme les nombres élémentaires des entiers naturels et des entiers relatifs car chaque entier naturel s'écrit de façon unique sous la forme d'un enchainement de produits de nombres premiers. Ce principe repose sur le théorème fondamentale de l'arithmétique.
2) Les nombres pairs et impairs
Bien que cette notion de parité soit vue depuis la classe de primaire, elle se définit désormais de la façon suivante :
Définition : On considère un entier relatif \(\displaystyle n\). Si \(\displaystyle n\) est divisible par 2 ou si \(\displaystyle n\) est un multiple de 2, on dit que \(\displaystyle n\) est pair. Sinon, on dit que \(\displaystyle n\) est impair.
Si \(\displaystyle n\) est pair, il existe un entier relatif \(\displaystyle k\) tel que \(\displaystyle n=2k\). Si \(\displaystyle n\) est impair, il existe un entier relatif \(\displaystyle k\) tel que \(\displaystyle n=2k+1\).
Propriété (admise) : La somme de deux nombres pairs est un nombre pair. La somme de deux nombres impairs est un nombre pair. La somme d'un nombre pair et d'un nombre impair est un nombre impair.
Propriété (démontrée) : Si \(\displaystyle n\) est un nombre pair, alors \(\displaystyle n^2\) est pair. Si \(\displaystyle n\) est un nombre impair, alors \(\displaystyle n^2\) est impair.
Démonstration à savoir : Démontrons la propriété précédente.
Si \(\displaystyle n\) est pair, on peut écrire \(\displaystyle n=2k\) avec \(\displaystyle k\) étant un entier relatif. Alors \(\displaystyle n^2=\left(2k\right)^2=2k\times2k=2\times2k^2\).
Donc 2 divise \(\displaystyle n^2\), d'où \(\displaystyle n^2\) est pair. Si \(\displaystyle n\) est impair, on peut écrire \(\displaystyle n=2k+1\) avec \(\displaystyle k\) étant un entier relatif. Alors \(\displaystyle n^2=\left(2k+1\right)^2=\left(2k\right)^2+2\times2k\times1+1^2\), ou encore \(\displaystyle n^2=4k^2+4k+1\).
Ainsi, \(\displaystyle n^2=2\left(2k^2+2k\right)+1\). On en déduit que \(\displaystyle n^2\) est impair.
Réciproquement, si \(\displaystyle n^2\) est pair alors \(\displaystyle n\) est pair. Et si \(\displaystyle n^2\) est impair, alors \(\displaystyle n\) est impair.