I) Mise en situation
Chaque jour, que ce soit dans la vie personnelle ou professionnelle, nous sommes confrontés aux mouvements de quelques objets qui nous entourent. La Terre elle-même est en mouvement.
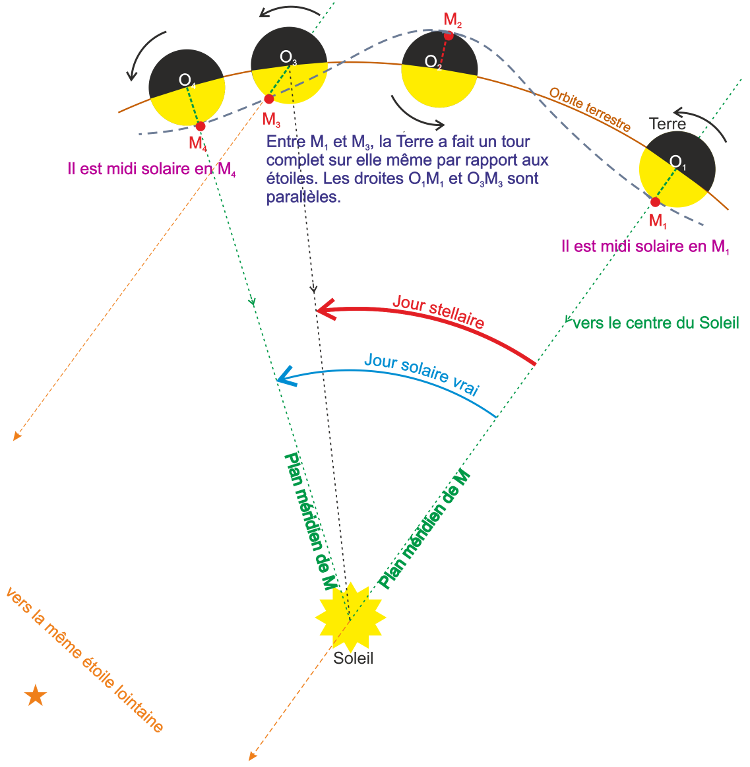
Les études des mouvements font appels aux lois de la physique et sont accompagnées par des calculs et schémas géométriques.
Ces derniers demandent des connaissances particulières qui sont apprises dés les premières années du collège. On parle des symétries axiales et centrales.
D'autres transformations sont nécessaires et vont s'ajouter à notre catalogue. Ce qui fait l'objet de cette séquence.
Pour entamer ce catalogue, nous proposons ici l'activité n°8 : activité n°8 et son annexe.
II) La symétrie axiale
La symétrie axiale peut être définie de la façon suivante :
Définition : Transformer une figure par symétrie axiale revient à créer l'image de cette figure par rapport à un axe.
Définition : Le symétrique d'un point \(\displaystyle A\) par une symétrie axiale d'axe \(\displaystyle \left(D\right)\) est le point \(\displaystyle A'\) tel que la droite \(\displaystyle \left(D\right)\) soit la médiatrice du segment \(\displaystyle \left[AA'\right]\).
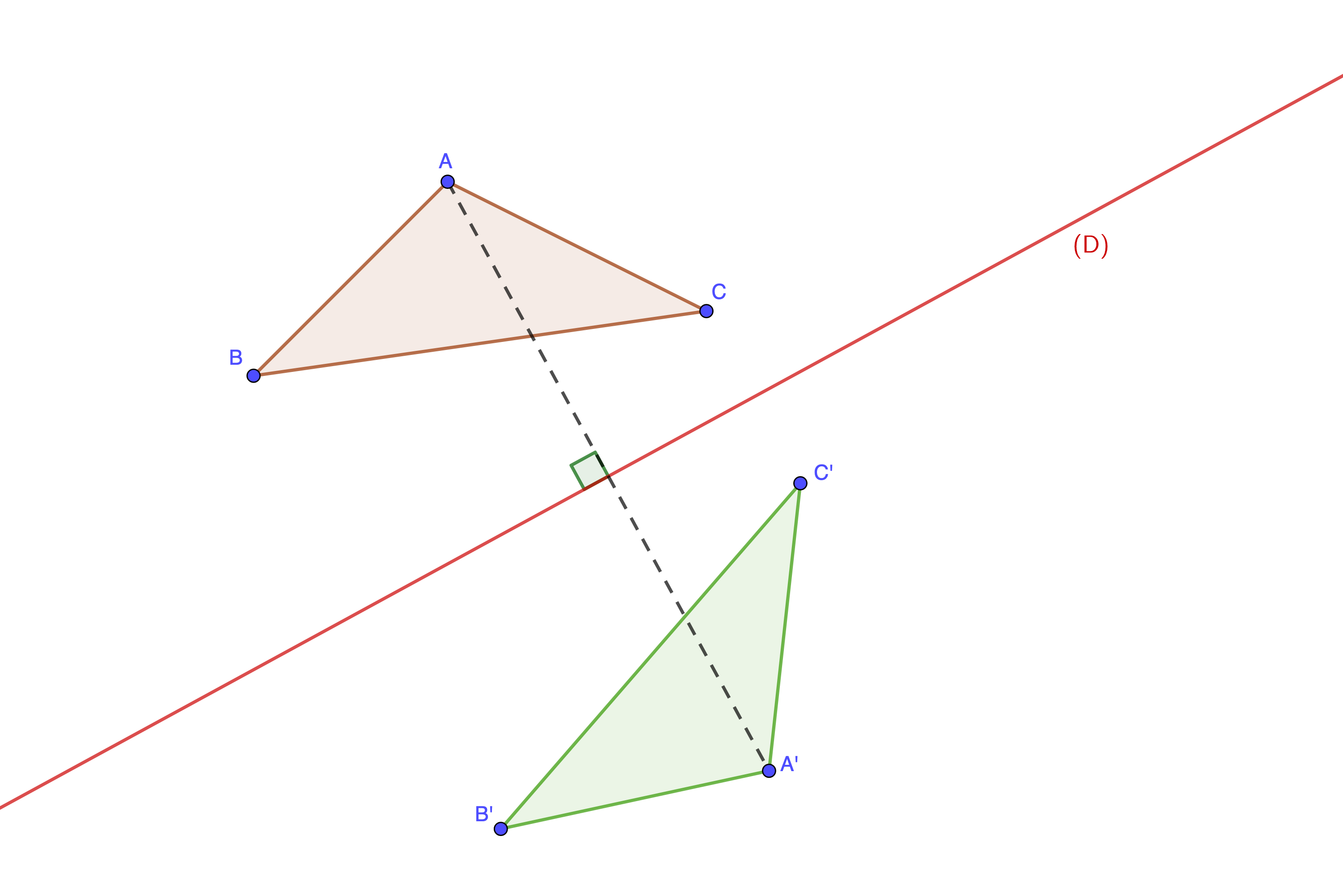
On rappelle ensuite les différentes propriétés liées à la symétrie axiale :
Propriété : Dans une symétrie axiale, le symétrique d'une droite est une droite. On dit que la symétrie axiale conserve l'alignement et le parallélisme.
Propriété : Dans une symétrie axiale, le symétrique d'un segment est un segment de même longueur. On dit que la symétrie axiale conserve les distances.
Propriété : Dans une symétrie axiale, le symétrique d'un angle est un angle de même mesure. On dit que la symétrie axiale conserve les angles.
Propriété : Dans une symétrie axiale, deux figures symétriques sont superposables et ont donc la même aire. On dit que la symétrie axiale conserve les aires.
III) La symétrie centrale
La symétrie centrale peut être définie de la façon suivante :
Définition : Deux figures sont symétriques par rapport à un point \( \displaystyle O\) lorsqu'elles se superposent en effectuant un demi-tour autour de ce point. Le point \( \displaystyle O\) est appelé le centre de la symétrie.
Définition : Par la symétrie de centre \( \displaystyle O\), le symétrique d'un point \( \displaystyle M\) distinct de \( \displaystyle O\) est le point \( \displaystyle M'\) tel que \( \displaystyle O\) soit le milieu du segment \( \displaystyle \left[MM'\right]\). Le symétrique du point \( \displaystyle O\) est le point \( \displaystyle O\).
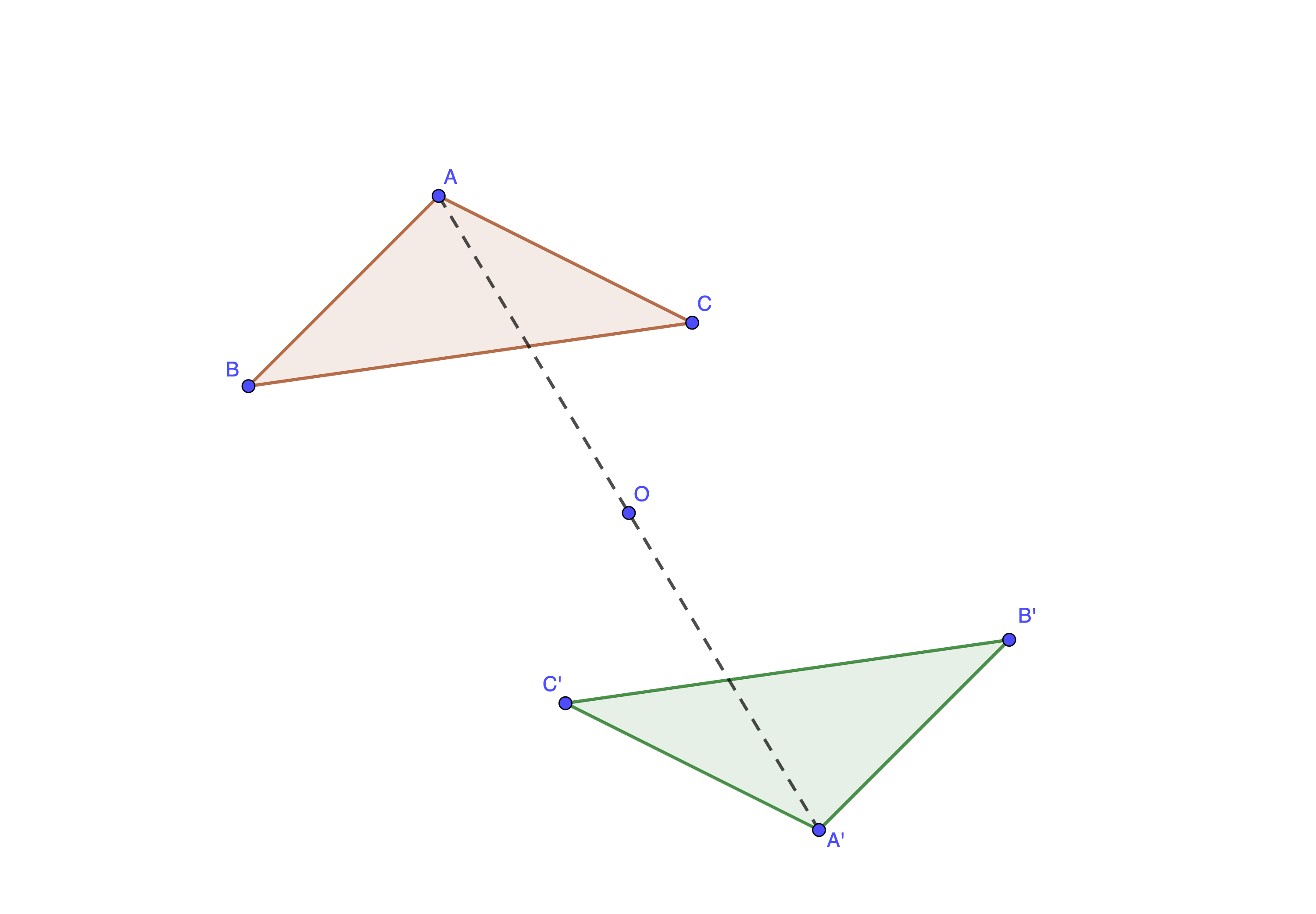
On rappelle ensuite les différentes propriétés liées à la symétrie centrale :
Propriété : Dans une symétrie centrale, le symétrique d'une droite est une droite. On dit que la symétrie centrale conserve l'alignement et le parallélisme
Propriété : Dans une symétrie centrale, le symétrique d'un segment est un segment de même longueur. On dit que la symétrie centrale conserve les distances.
Propriété : Dans une symétrie centrale, le symétrique d'un angle est un angle de même mesure. On dit que la symétrie centrale conserve les angles.
Propriété : Dans une symétrie centrale, deux figures symétriques sont superposables et ont donc la même aire. On dit que la symétrie centrale conserve les aires.
IV) La translation
La translation peut être définie de la façon suivante :
Définition : Transformer une figure par translation, c'est créer l'image de cette figure par déplacement, selon deux points donnés.
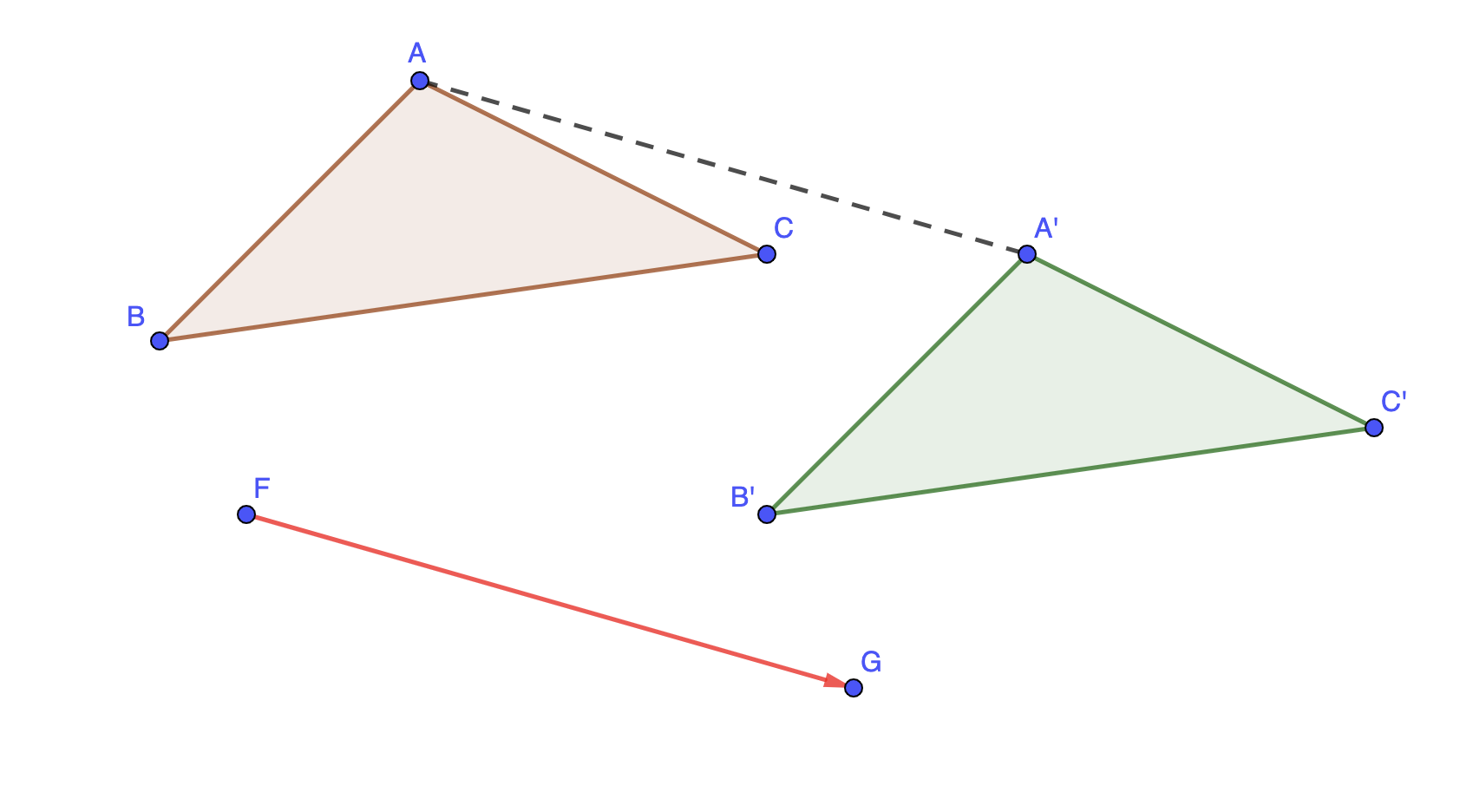
On rappelle ensuite les différentes propriétés liées à la translation :
Propriété : L’image du point \(\displaystyle M\) par la translation qui transforme \(\displaystyle A\) en \(\displaystyle B\) est le point \(\displaystyle M’\), tel que les segments \(\displaystyle \left[MB\right]\) et \(\displaystyle \left[AM’\right]\) ont le même milieu. Si les points ne sont pas alignés, alors \(\displaystyle ABM’M\) est un parallélogramme.
Propriété : Dans une translation, l'image d'une droite est une droite. On dit que la translation conserve l'alignement et le parallélisme.
Propriété : Dans une translation, l'image d'un segment est un segment de même longueur. On dit que la translation conserve les distances.
Propriété : Dans une translation, l'image d'un angle est un angle de même mesure. On dit que la translation conserve les angles.
Propriété : Dans une translation, deux figures symétriques sont superposables et ont donc la même aire. On dit que la translation conserve les aires.
V) La rotation
La rotation peut être définie de la façon suivante :
Définition : Transformer une figure par rotation, c'est créer l'image de cette figure en la tournant, selon un centre, un angle et un sens.
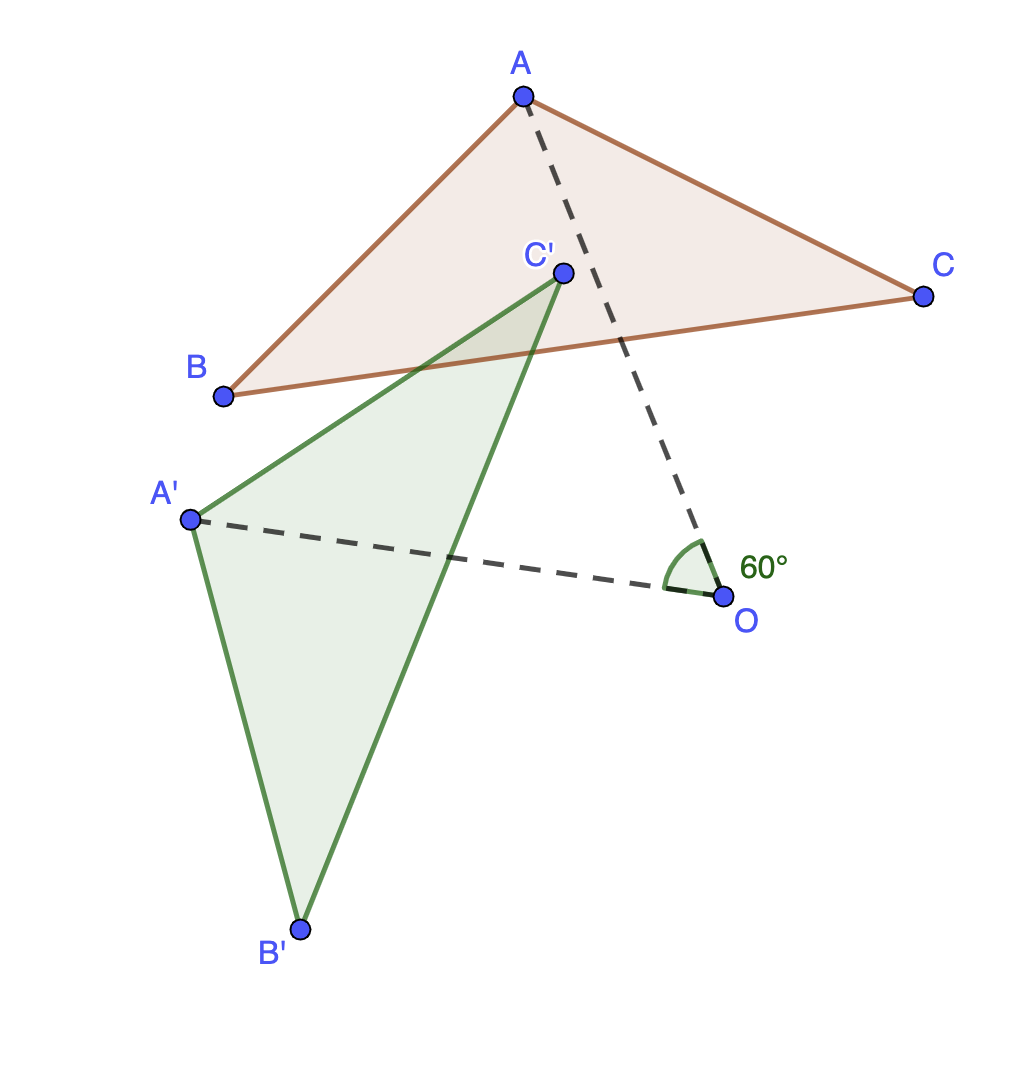
On rappelle ensuite les différentes propriétés liées à la rotation :
Propriété : On considère deux points distincts \(\displaystyle O\) et \(\displaystyle M\). L’image du point \(\displaystyle M\) par la rotation de centre \(\displaystyle O\) et d’angle \(\displaystyle \alpha\) est le point \(\displaystyle M’\) tel que \(\displaystyle OM’=OM\) et \(\displaystyle \widehat{MOM'}=\alpha\).
Propriété : Dans une rotation, l'image d'une droite est une droite. On dit que la rotation conserve l'alignement et le parallélisme.
Propriété : Dans une rotation, l'image d'un segment est un segment de même longueur. On dit que la rotation conserve les distances.
Propriété : Dans une rotation, l'image d'un angle est un angle de même mesure. On dit que la rotation conserve les angles.
Propriété : Dans une rotation, deux figures symétriques sont superposables et ont donc la même aire. On dit que la rotation conserve les aires.
VI) L'homothétie
L'homothétie peut être définie de la façon suivante :
Définition : Transformer une figure par homothétie, c'est créer l'image de cette figure en la déplaçant par rapport à un centre et en modifiant les longueurs selon un rapport \(\displaystyle k\).
Définition : L'image d'un point \(\displaystyle M\) par une homothétie de centre \(\displaystyle O\) et de rapport \(\displaystyle k > 0\) est le point \(\displaystyle M'\) tel que \(\displaystyle OM'=kOM\).
Définition : L'image d'un point \(\displaystyle M\) par une homothétie de centre \(\displaystyle O\) et de rapport \(\displaystyle k < 0\) est le point \(\displaystyle M'\) (du côté opposé à \(\displaystyle M\) par rapport à \(\displaystyle O\)) tel que \(\displaystyle OM'=-kOM\).
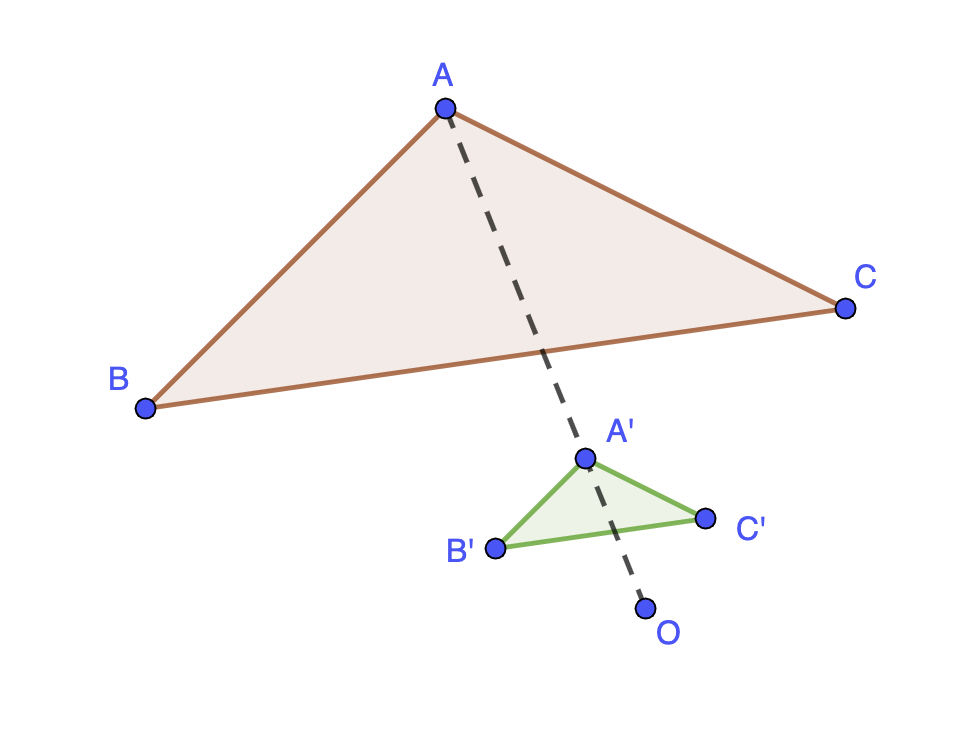
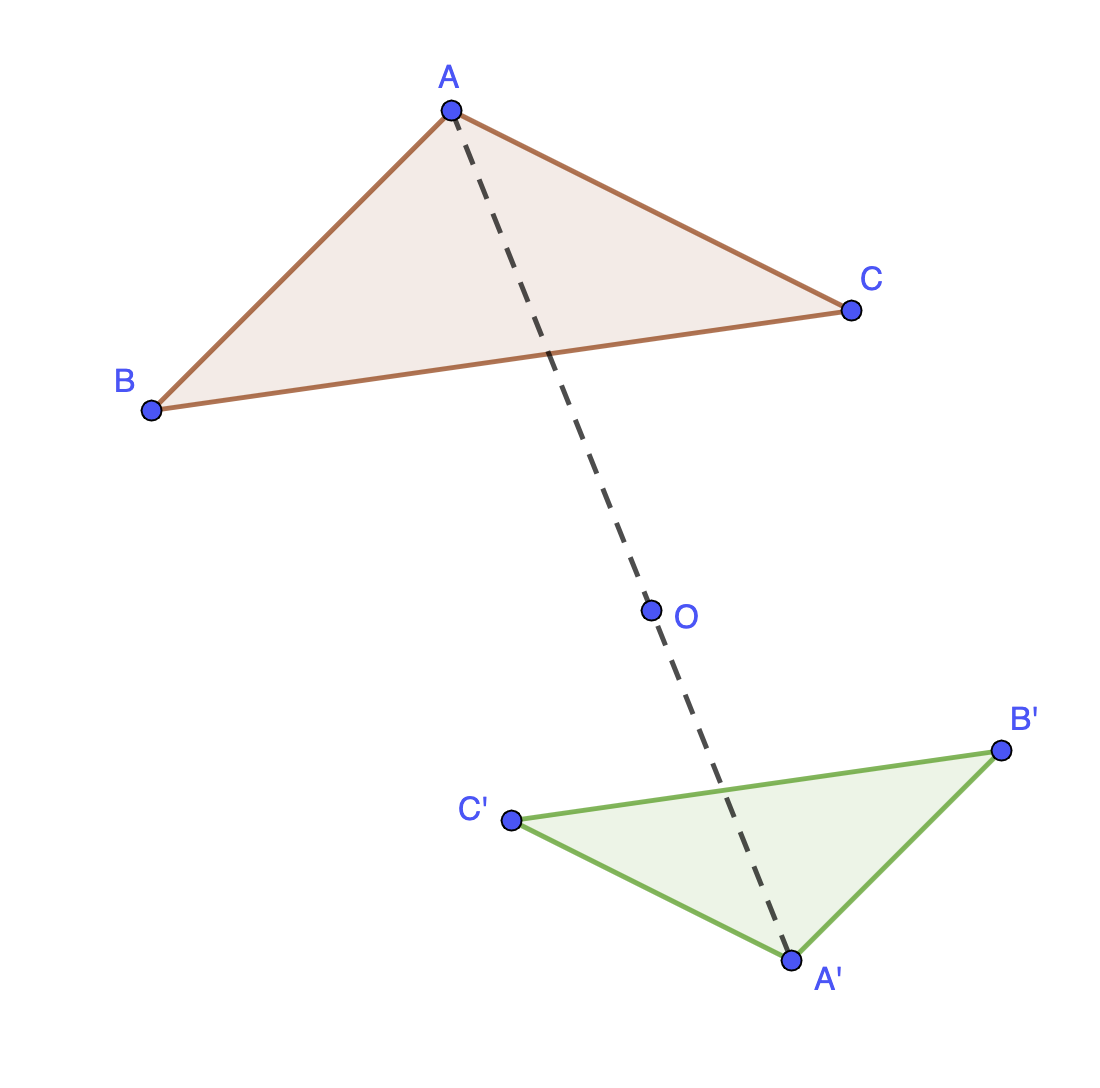
Remarque : Lorsque \(\displaystyle k > 1\) (ou \(\displaystyle k < -1\)), l'homothétie est un agrandissement. Lorsque \(\displaystyle 0 < k < 1\) (ou \(\displaystyle -1 < k < 0\)), l'homothétie est une réduction.
On donne les différentes propriétés liées à l'homothétie :
Propriété : L'image \(\displaystyle M'\) par une homothétie de centre \(\displaystyle O\) d'un point \(\displaystyle M\) est aligné avec \(\displaystyle O\) et \(\displaystyle M\).
Propriété : Dans une homothétie de rapport \(\displaystyle k=1\), aucune transformation n'est effectuée.
Propriété : Réaliser une homothétie de rapport \(\displaystyle k=-1\) revient à effectuer une symétrie centrale.