I) Mise en situation
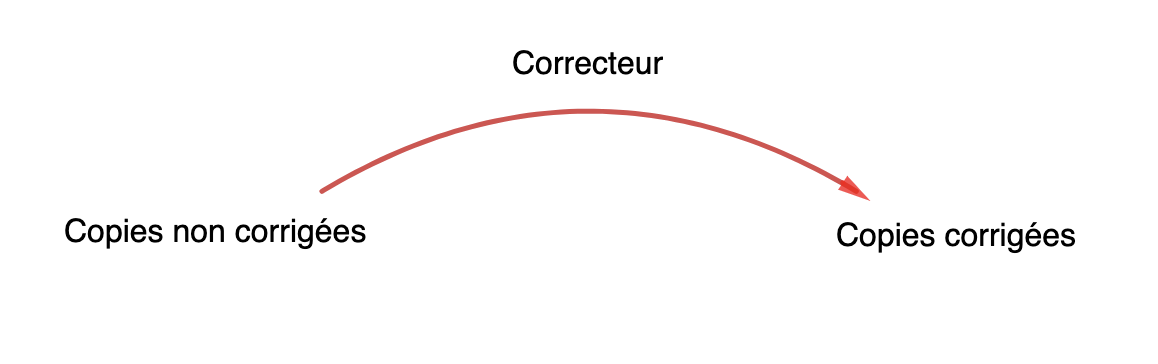
Abordons la notion de fonction à l'aide d'un métier. Prenons celui d'enseignant. Le métier d'enseignant, comme beaucoup d'autres professions, sont pourvues de multi-fonctions, de multi-tâches. Une en particulier consiste à corriger une copie.
Pour ce faire, il procède en trois étapes :
- L'enseignant prend une copie au niveau du tas de copies non corrigées.
- L'enseignant corrige, évalue et note la copie.
- L'enseignant la pose sur le tas de copies corrigées.
La situation peut être représentée de la façon suivante :
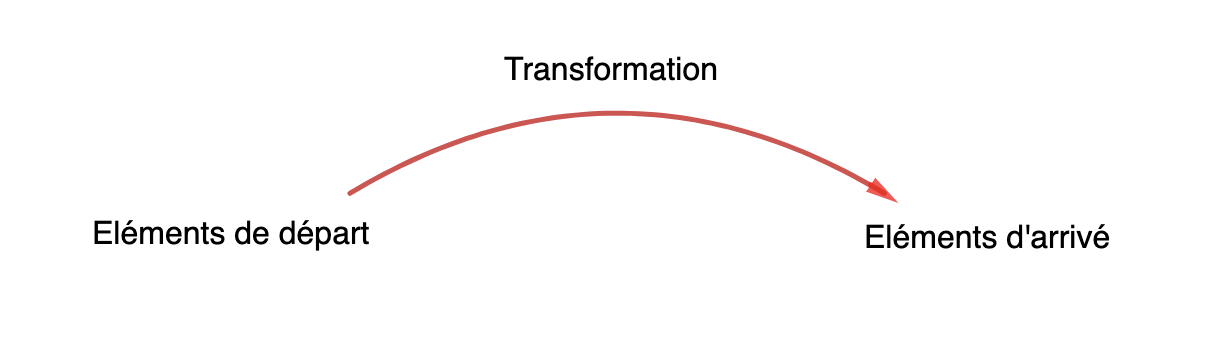
Ce schéma en trois parties peut se calquer sur plusieurs autres situations professionnelles. De manière générale, on retient la représentation suivante :
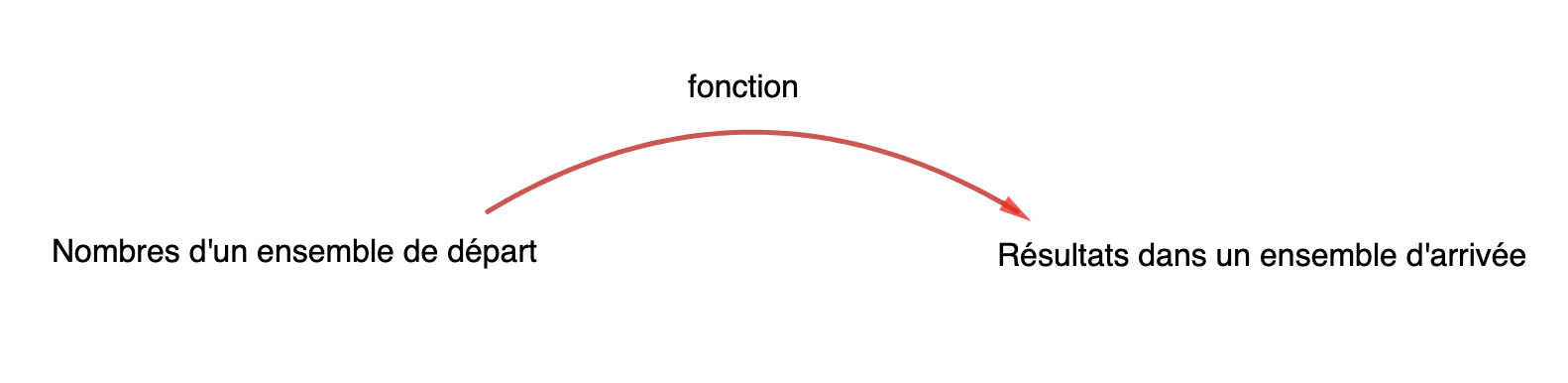
Il est possible aussi de le calquer sur des opérations mathématiques :
On imagine un ensemble de départ que l'on note \(\displaystyle D\) dans lequel se trouvent des nombres réels. On imagine un enchainement d'opérations qui consistera à prendre un nombre dans cet ensemble de départ, d'effectuer le calcul et de déposer ensuite le résultat dans un ensemble d'arrivé. On retrouve ici le schéma en trois étapes :
Il va falloir désormais utiliser un vocabulaire adéquat pour étudier une fonction en mathématiques.
II) Définitions et notations
La fonction se définit de la façon suivante :
Définition : Une fonction est le processus qui, à un nombre, fait correspondre un autre nombre unique.
Cette fonction est souvent nommée \(\displaystyle f\).
Le nombre de départ choisi est souvent représenté par la lettre \(\displaystyle x\). Comme c'est un nombre qui peut varier, on appele cela une variable. On dit ainsi que \(\displaystyle f\) dépend de la variable \(\displaystyle x\).
Exemple : Supposons que la fonction demande d'élever au carré le nombre de départ et de soustraire ensuite le résultat par 1. La fonction \(\displaystyle f\) se définit alors par \( \displaystyle f:x\longmapsto x^2-1\) ou encore \( \displaystyle f\left(x\right)=x^2-1\)
Pour chaque valeur de \(\displaystyle x\), on associe le résultat par la fonction \(\displaystyle f\). Les résultats peuvent être indiqués dans un tableau, appelé tableau de valeurs. Pour notre exemple, cela donne :
| \(\displaystyle x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| \(\displaystyle f\left(x\right)\) | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 | 24 |
Les résultats peuvent être aussi représentés sous forme d'un graphique. Dans un repère, on considère tous les points \(\displaystyle M\) de coordonnées \(\displaystyle \left(x;y\right)\) tels que pour chaque \(\displaystyle x\) on associe le résultat \(\displaystyle f\left(x\right)\). L'ensemble de tous ces points donne la courbe représentative de \(\displaystyle f\). Pour l'exemple, on aura :
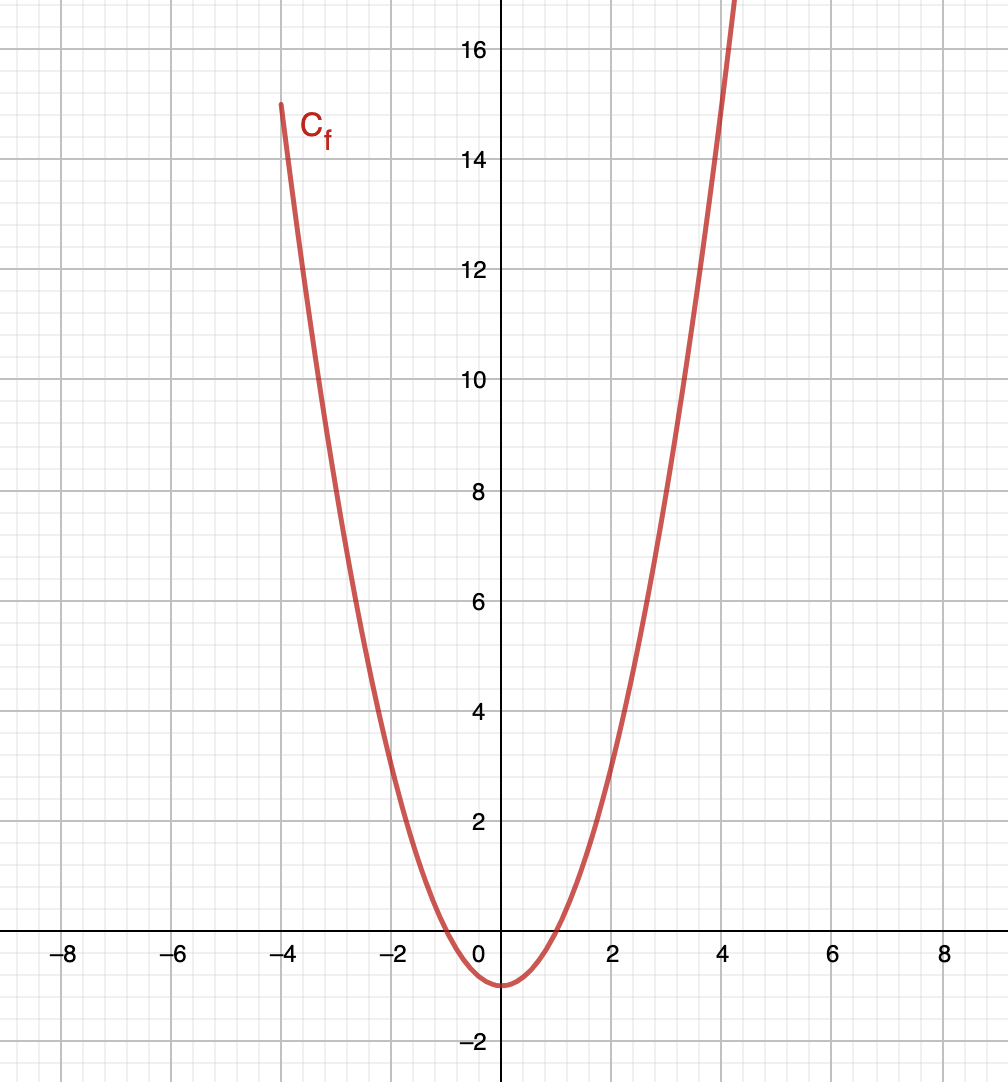
III) La notion d'image
L'image d'un nombre par une fonction se définit de la façon suivante :
Définition : Le résultat par la fonction \(\displaystyle f\) d'un nombre \(\displaystyle a\) correspond un nombre \(\displaystyle b\) et s'appelle l'image du nombre \(\displaystyle a\).
Il existe deux méthodes pour obtenir l'image d'un nombre par une fonction \(\displaystyle f\). Il existe la méthode algébrique et la méthode graphique.
La méthode algébrique consiste à effectuer le calcul. Si on a par exemple la fonction \(\displaystyle f\) définie par \(\displaystyle f\left(x\right)=x^3+2x-1\), et qu'on veuille l'image du nombre -3 par la fonction \(\displaystyle f\), alors cette image se note \(\displaystyle f\left(3\right)\) et se calcule par :
\(\displaystyle \begin{align*} f\left(x\right)&=x^3+2x-1 \\ f\left(3\right)&=3^3+2\times3-1 \\ &=27+6-1 \\ &=33-1 \\ &=32 \end{align*} \)
On a ainsi l'image de 3 par la fonction \(\displaystyle f\) est \(\displaystyle f\left(3\right)=32\).
La méthode graphique consiste à lire directement le résultat sur le graphique. Si on a par exemple la fonction \(\displaystyle f\) représentée par sa courbe \(\displaystyle \left(C_f\right)\) de la façon suivante :
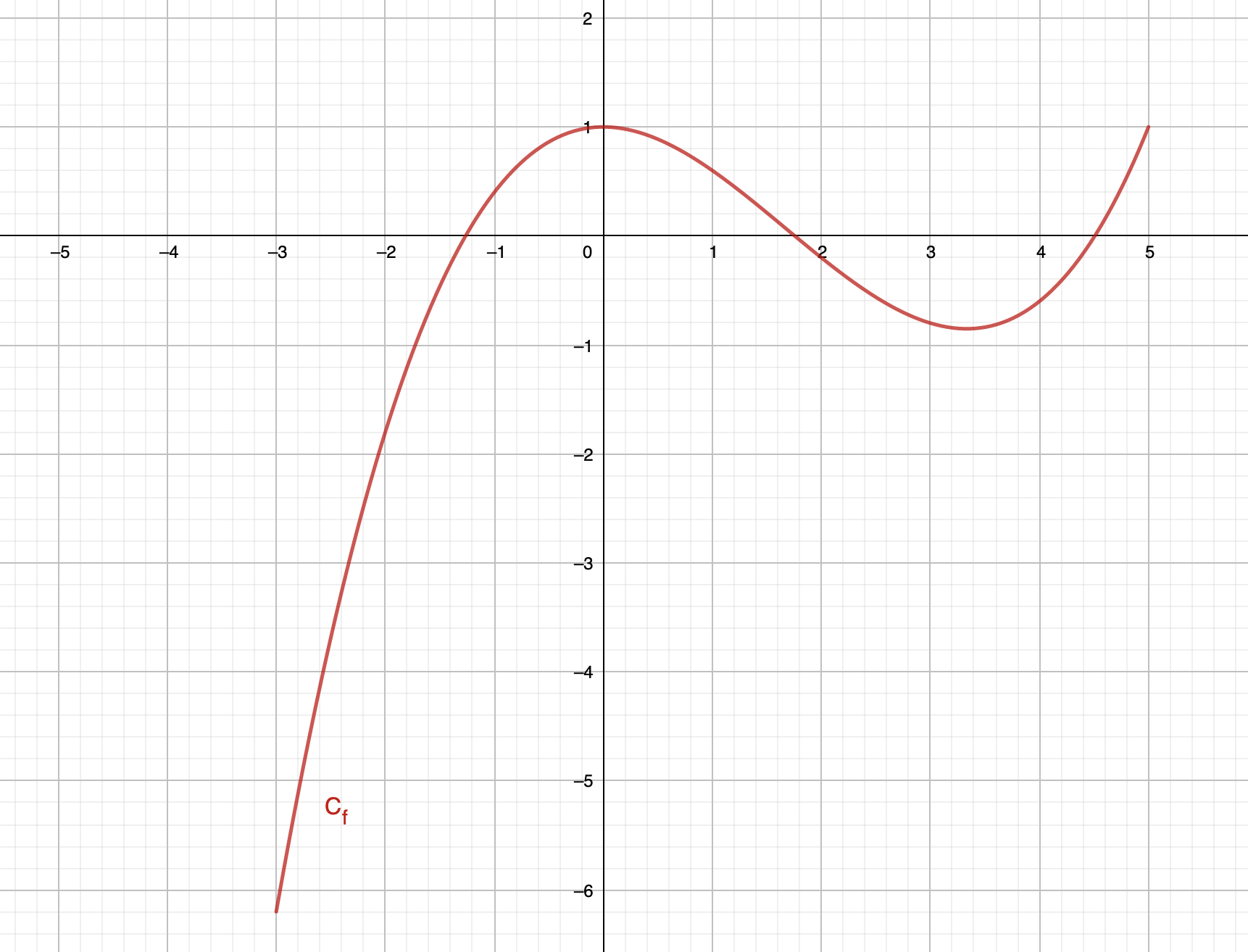
Si on veut lire l'image de 0 par la fonction \(\displaystyle f\), alors cela revient à lire graphiquement l'ordonnée du point \(\displaystyle M\) de la courbe \(\displaystyle \left(C_f\right)\) telle que l'abscisse du point est 0. Graphiquement, cela donne \(\displaystyle f\left(0\right)=1\).
IV) La notion d'antécédent
L'antécédent d'un nombre par une fonction se définit de la façon suivante :
Définition : Les nombres dont l'image est \(\displaystyle b\) par une fonction \(\displaystyle f\) s'appellent les antécédents de cette image.
Il existe deux méthodes pour obtenir l'image d'un nombre par une fonction \(\displaystyle f\). Il existe la méthode algébrique et la méthode graphique.
La méthode algébrique consiste à effectuer le calcul. Si on a par exemple la fonction \(\displaystyle f\) définie par \(\displaystyle f\left(x\right)=3x-1\), et qu'on veuille l'antécédent du nombre 4 par la fonction \(\displaystyle f\), alors cet antécédent se note \(\displaystyle x\) et se calcule par :
\(\displaystyle \begin{align*} f\left(x\right)&=3x-1 \\ 4&=3x-1 \\ -3x&=-4-1 \\ x&=\frac{5}{3} \end{align*} \)
On a ainsi l'antécédent de 4 par la fonction \(\displaystyle f\) est \(\displaystyle x=\frac{5}{3}\).
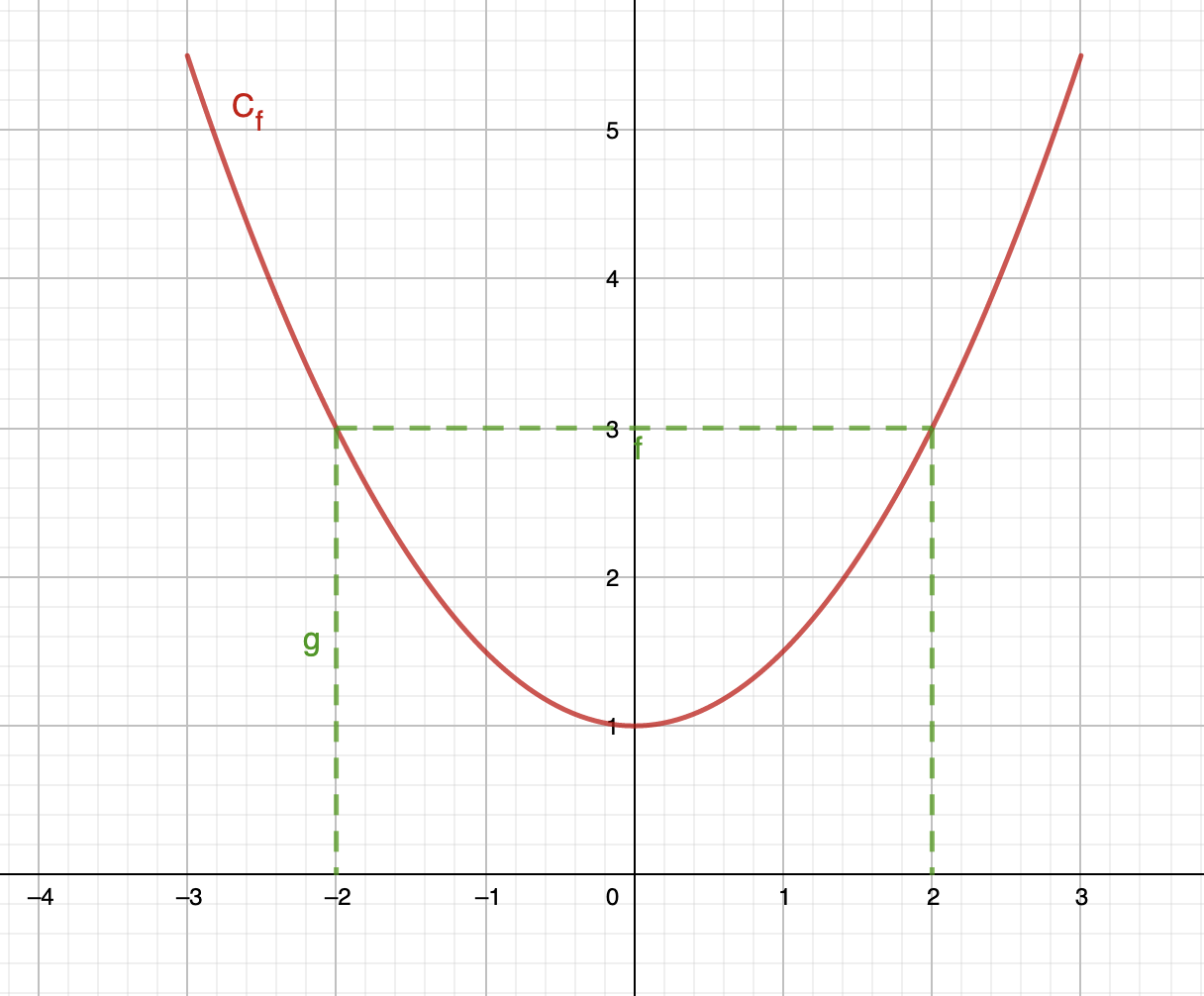
La méthode graphique consiste à lire directement le résultat sur le graphique. Si on a par exemple la fonction \(\displaystyle f\) représentée par sa courbe \(\displaystyle \left(C_f\right)\) de la façon suivante :

Si on veut lire les antécédents de 3 par la fonction \(\displaystyle f\), alors cela revient à lire graphiquement les abscisses des points \(\displaystyle M\) de la courbe \(\displaystyle \left(C_f\right)\) telle que les ordonnées soient 3. Graphiquement, cela donne \(\displaystyle x=-2\) et \(\displaystyle x=2\) :