I) Mise en situation
Pour introduire la notion d'agrandissement et de réduction, on considère le principe de fonctionnement de l'oeil à partir de l'activité suivante : activité n°4.
La notion d'agrandissement et de réduction est issue des configurations de Thalès. Elles seront rappelées très brièvement danc cette séquence.
II) Les configurations de Thalès
La configuration de Thalès la plus souvent rencontrée est proposée dans le schéma ci-dessous. On y apperçoit deux triangles.
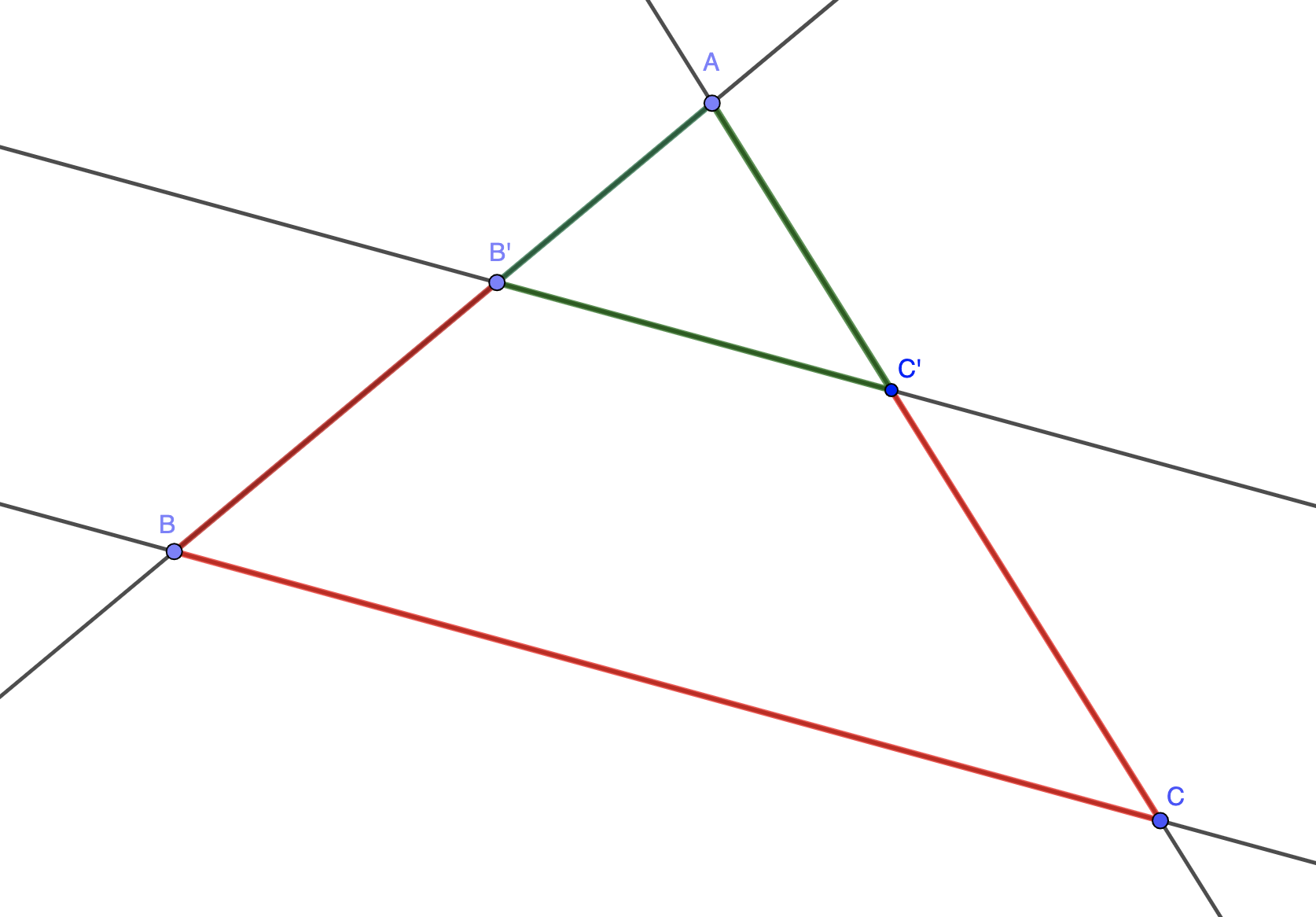
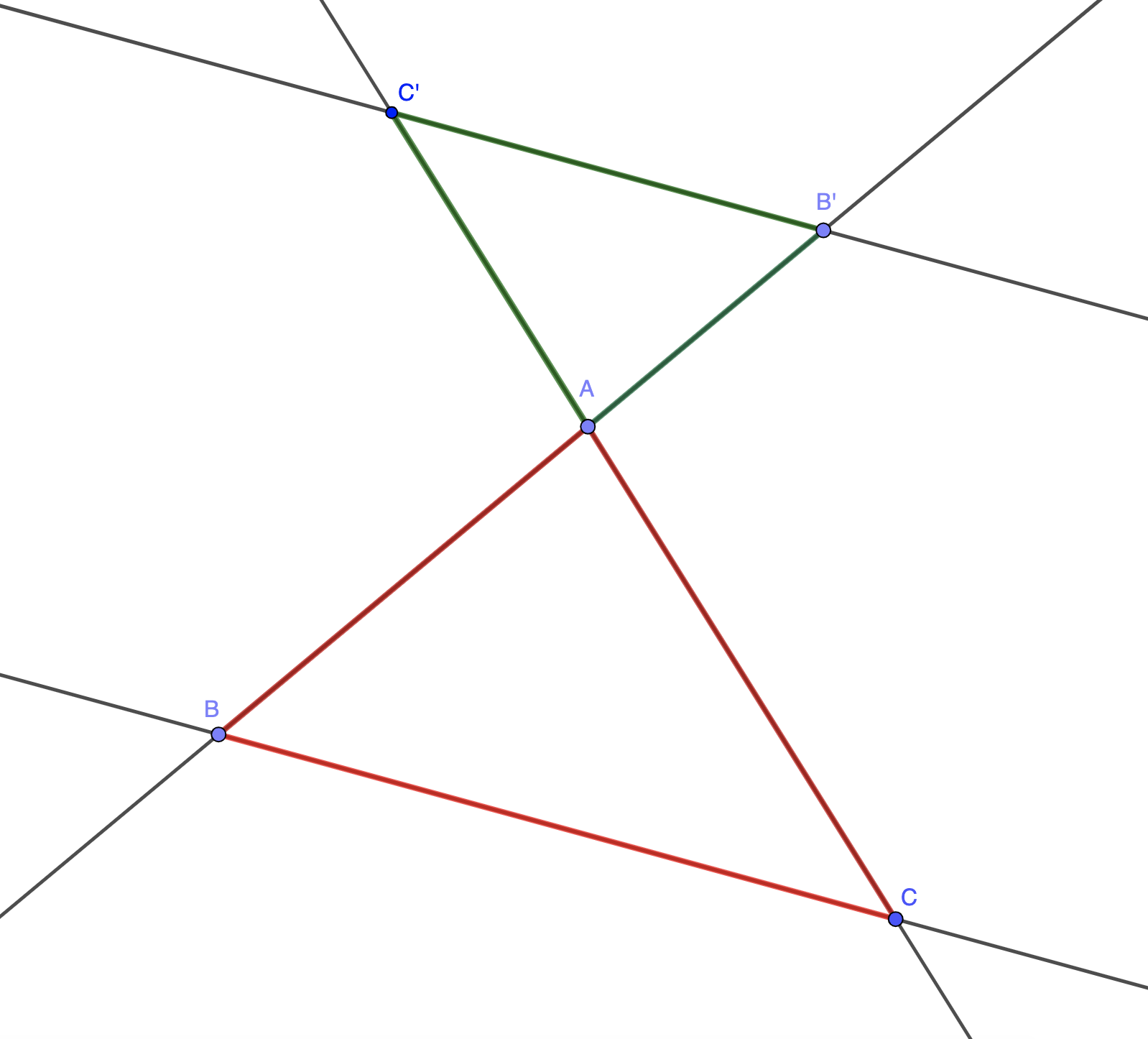
Le théorème de Thalès permet d'écrire des égalités de rapports de distances. Par conséquent, les longueurs des côtés sont proportionnelles, deux à deux.
Définition : Deux triangles sont dits semblables si leurs longueurs de côté sont proportionnels deux à deux.
Définition : Deux triangles sont dits semblables si leurs angles sont égaux.
III) Agrandissement et réduction
Dans la configuration de Thalès, le triangle disposant des plus grandes longueurs devient un agrandissement de l'autre, ayant donc les longueurs les plus petites. Réciproquement, le triangle avec les plus petites longueurs devient une réduction du triangle aux plus grandes longueurs.
Propriété : Dans un agrandissement, le coefficient d'agrandissement, noté \(\displaystyle k\) est tel que \(\displaystyle k > 1\).
Propriété : Dans une réductions, le coefficient de réduction, noté \(\displaystyle k\) est tel que \(\displaystyle k < 1\).
Propriété : Lors d'une réduction (ou d'un agrandissement) de coefficient \(\displaystyle k\) d'une longueur \(\displaystyle AB\) en \(\displaystyle A'B'\), la relation qui lie les deux longueurs s'écrit \(\displaystyle A'B'=kAB\).
Propriété : Lors d'une réduction (ou d'un agrandissement) de coefficient \(\displaystyle k\) d'une aire de surface \(\displaystyle A\) en \(\displaystyle A'\), la relation qui lie les deux aires s'écrit \(\displaystyle A'=k^2A\).
Propriété : Lors d'une réduction (ou d'un agrandissement) de coefficient \(\displaystyle k\) d'un volume \(\displaystyle V\) en \(\displaystyle V'\), la relation qui lie les deux volume s'écrit \(\displaystyle V'=k^3V\).