I) Mise en situation
Le 31 mars 1989, est déposé au sommet de la Tour Eiffel, le drapeau tricolore traduisant l'ouverture inaugurale officielle du monument.
Elle reste aujourd'hui le monument le plus visité au monde. Le record a été battu en 2014 avec 7 097 302 visiteurs. En dehors de la montée des marches et de la visite des étages, de nombreuses attractions s'y sont développées comme par exemple, le restaurant Le Jules Verne où la gastronomie française y est, parait-il, très appréciée.
Même si ses dimensions sont parfaitement connues aujourd'hui comme l'indique le schéma suivant, est-il possible tout de même de mesurer la hauteur de la tour en restant au sol ?
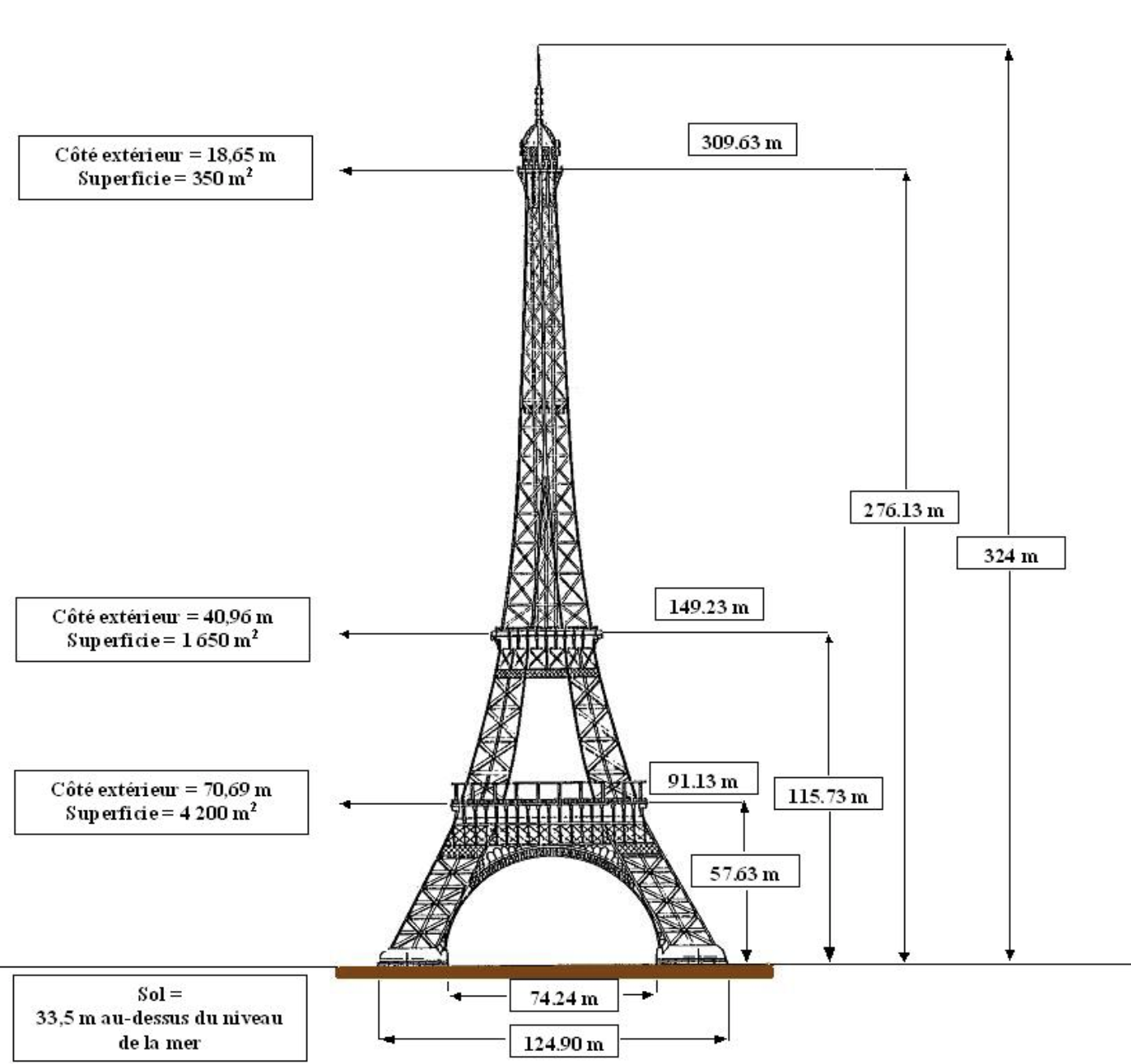
Pour s'en convaincre, l'idéal serait de se rendre sur les Champs de Mars et de tenter d'expérience. En attendant, nous allons expérimenter une méthode par la mesure de la hauteur d'un arbre, via l'activité suivante : activité n°2
II) Une méthode de mesure
Une méthode consiste à utiliser un objet (un crayon, un doight, ...) qui épouse parfaitement l'angle de vue comme le montre la photographie et le schéma suivant :

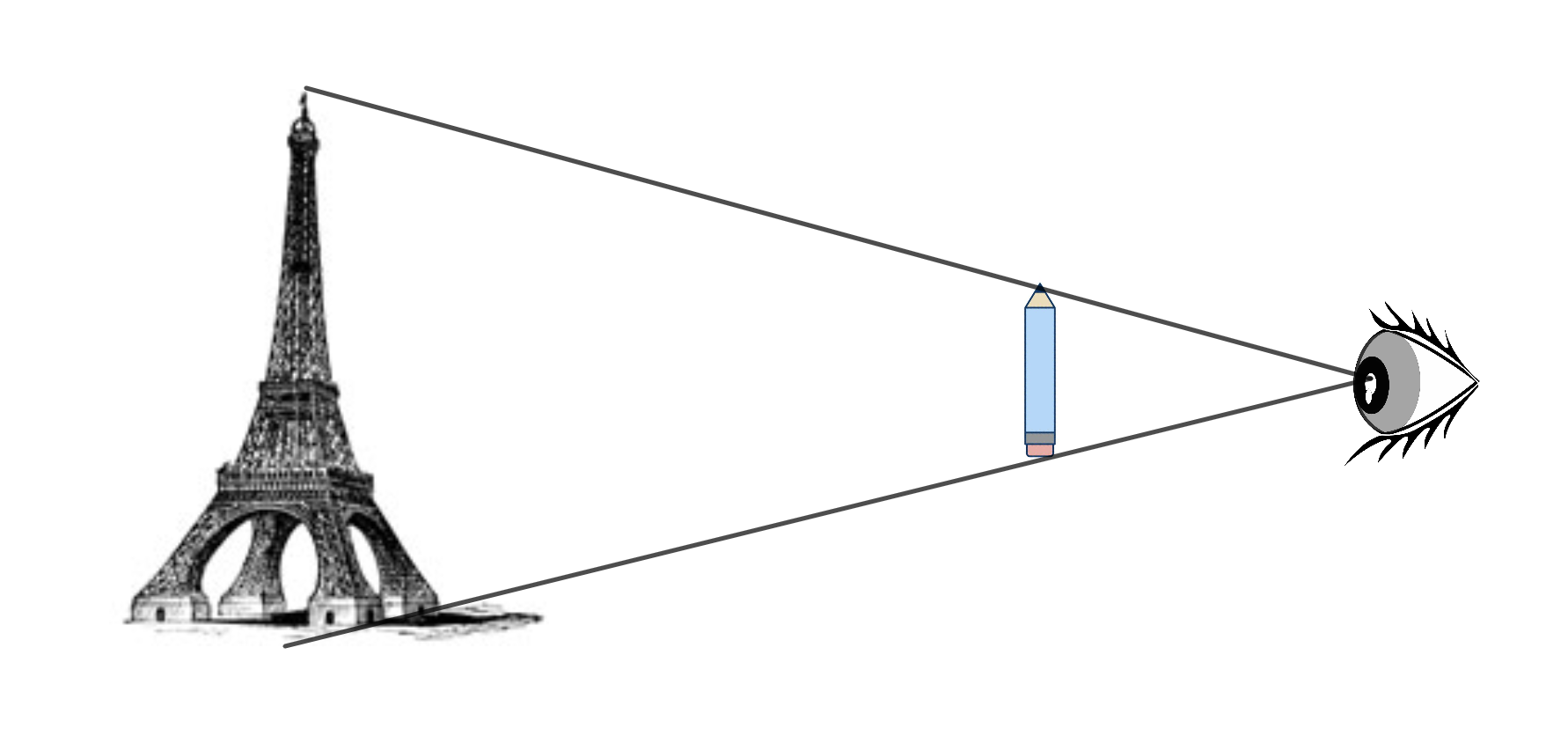
Ainsi, en connaissant la distance qui sépare le pied de la tour avec la personne qui utilise la prise de vue, et en connaissant la distance que sépare l'oeil au pied du crayon, ainsi que la dimension de crayon lui-même, il est alors possible d'en déduire la hauteur de la tour, en utilisant un théorème, connu sous le nom du théorème de Thalès, qui n'en est pourtant pas l'auteur.
Que dit ce théorème ?
III) Le théorème de Thalès
On considère la figure suivante :
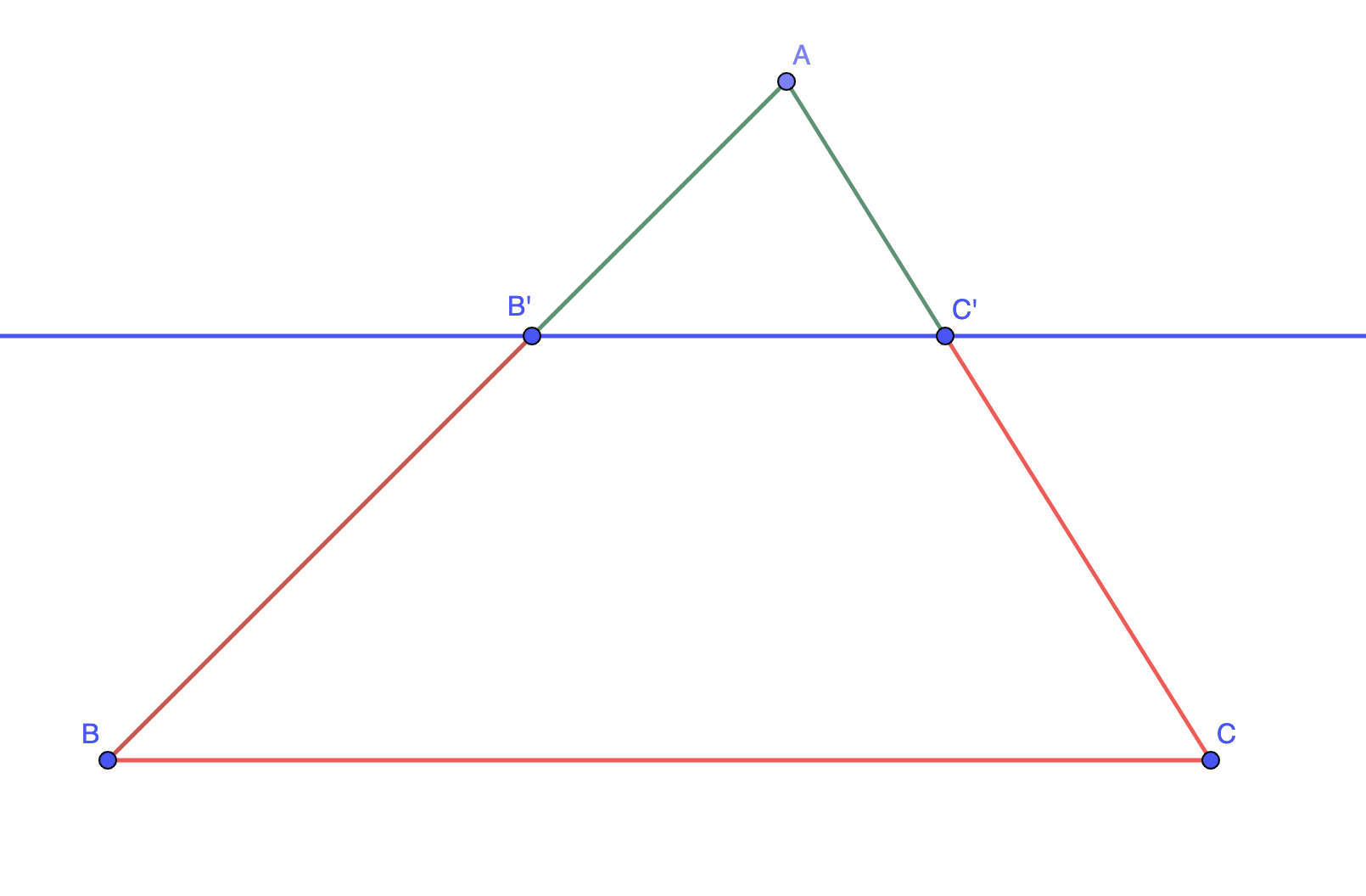
Propriété : (Théorème admis de Thalès) Dans un triangle \( \displaystyle ABC\), où \( \displaystyle B'\) est un point de \( \displaystyle \left(AB\right)\) et \( \displaystyle C'\) est un point de \( \displaystyle \left(AC\right)\), et où les droites \( \displaystyle \left(B'C'\right)\) et \( \displaystyle \left(BC\right)\) sont parallèles, alors \( \displaystyle \frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}\).
IV) Application du théorème sur le calcul d'une longueur
Considérons maintenant les deux cas suivants :
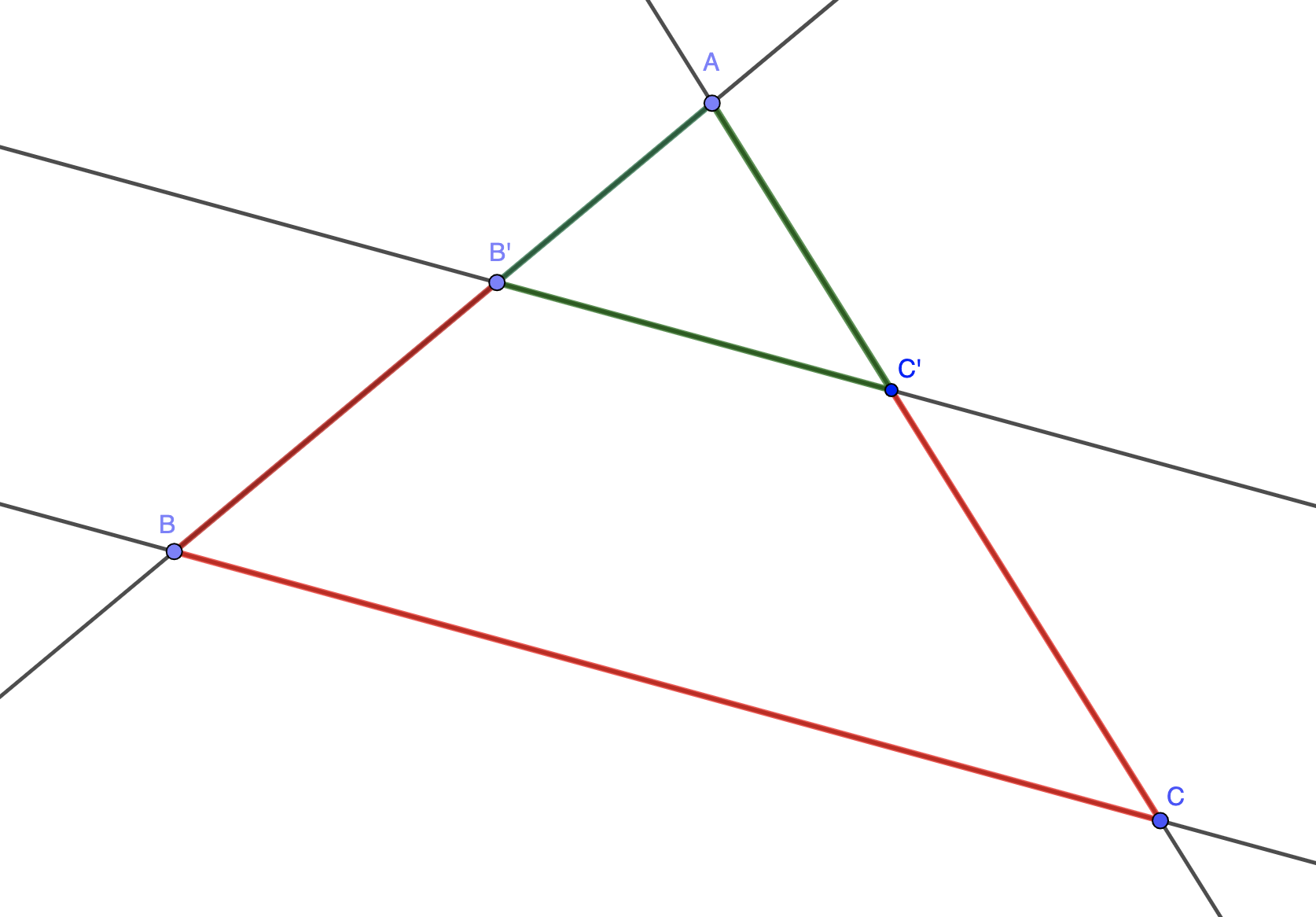
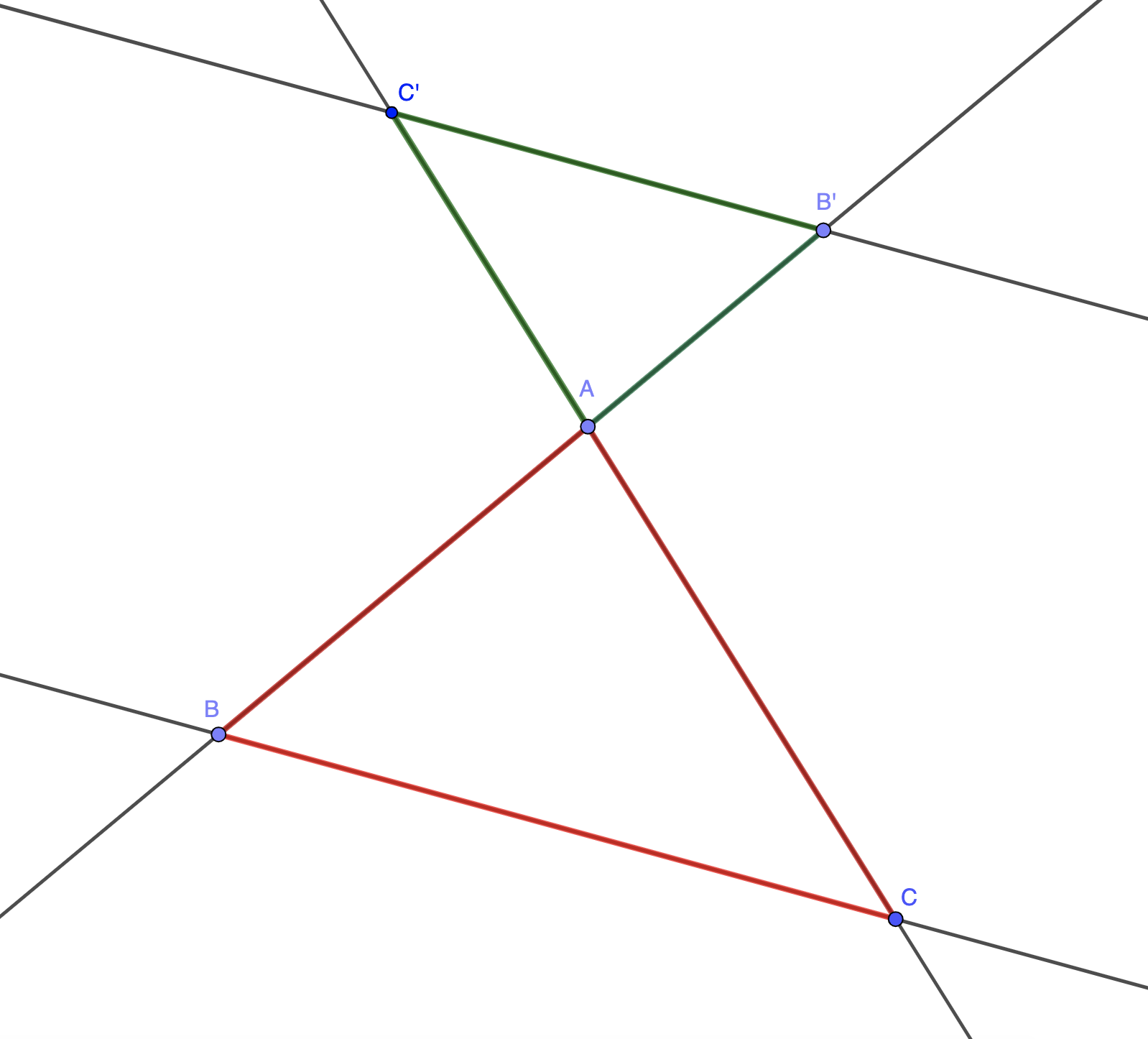
Propriété : (admise) Si deux droites parallèles coupent deux droites sécantes, alors elles déterminent deux triangles dont les côtés correspondants ont des longueurs proportionnelles.
Dans ces deux configurations, les triangles \( \displaystyle \color{green}{AB'C'}\) et \( \displaystyle \color{red}{ABC}\) ont des côtés deux à deux proportionnels. Les rapports entre eux sont donc égaux :
Ainsi, si \( \displaystyle \left(BB'\right)\), et \( \displaystyle \left(CC'\right)\) sont sécantes en \( \displaystyle A\) et \( \displaystyle \left(BC\right)\) parallèle à \( \displaystyle \left(B'C'\right)\), alors \( \displaystyle \frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}\).
Remarque importante : On note toujours que dans de tels cas, les triangles formés sont des triangles semblables.
V) Application du théorème sur le calcul de la longeur de la tour.
On repart du schéma suivant sur lequel nous avons placé les points :
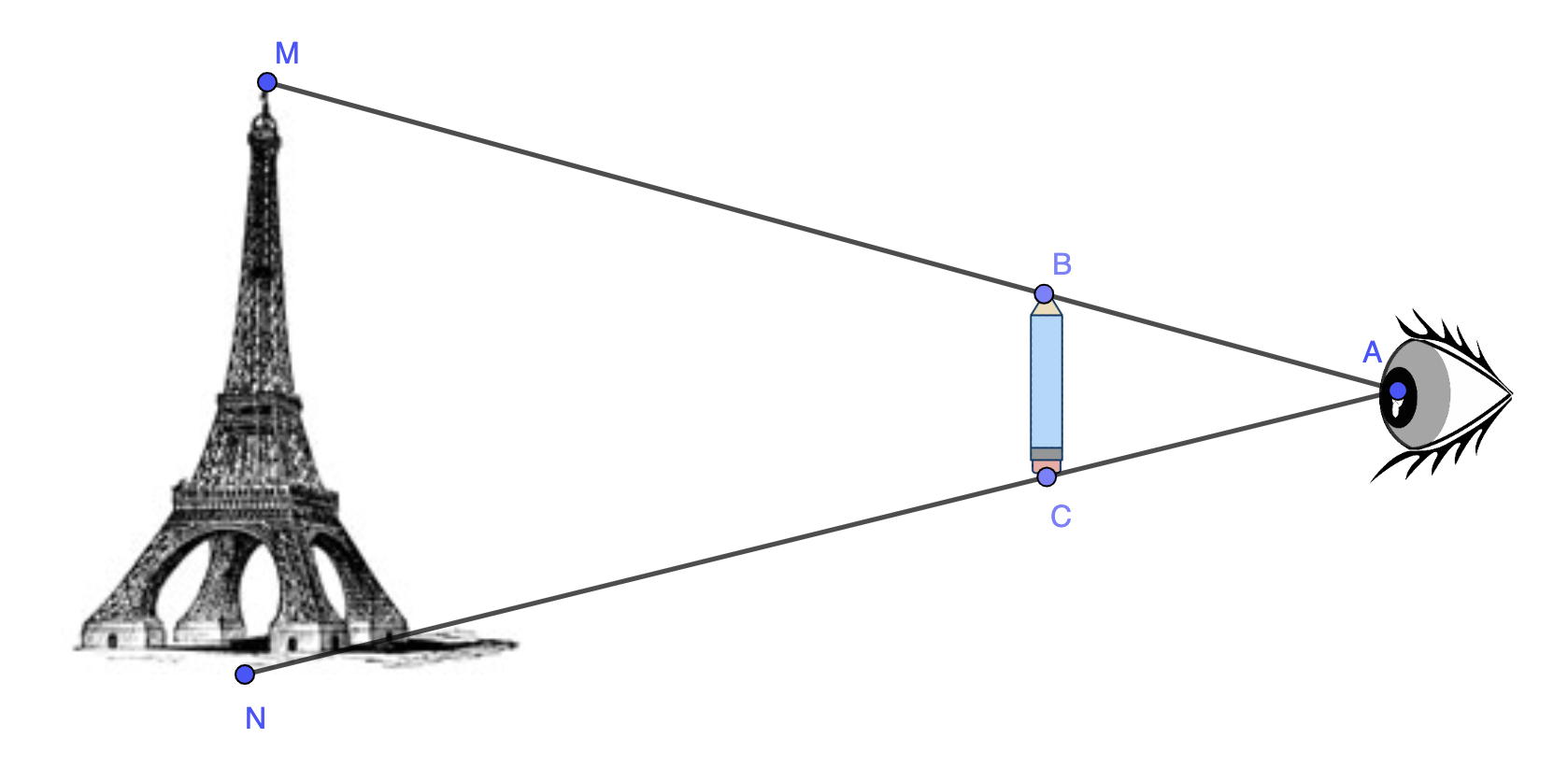
En partant du principe ou le crayon est placé de façon parallèle à la verticale, comme l'est la tour Eiffel, alors on a \( \displaystyle \left(MN\right)//\left(BC\right)\)
Ainsi, d'après le théoème de Thalès, comme \( \displaystyle \left(MN\right)//\left(BC\right)\) alors on a \( \displaystyle \frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\).
Nous n'avons besoin ici que de la relation \( \displaystyle \frac{AN}{AC}=\frac{MN}{BC}\).
On peut écrire alors \( \displaystyle MN=\frac{BC\times AN}{AC}\)
La prise de mesure nous donne facilement la longueur du crayon : \( \displaystyle BC=15\)cm la distance de l'oeil au pied du crayon : \( \displaystyle AC=20\)cm et la distance de l'observateur à la tour : \( \displaystyle AN=430\)m.
On a alors le calcul : \( \displaystyle MN=\frac{0,15\times430}{0,2}\). Ce qui nous donne environ 322,5m. Une estimation qui est très proche de la réalité.
VI) La réciproque du théorème de Thalès
La réciproque du théorème de Thalès est utilisé uniquement pour montrer que deux droites sont parallèles.
Réciproque admise du théorème de Thalès : On considère deux droites \( \displaystyle d\) et \( \displaystyle d'\) sécantes en \( \displaystyle A\), deux points \( \displaystyle B\) et \( \displaystyle M\) de la droite \( \displaystyle d\) distincts de \( \displaystyle A\) et deux points \( \displaystyle C\) et \( \displaystyle N\) de la droite \( \displaystyle d'\), distincts de \( \displaystyle A\). Alors Si \( \displaystyle \frac{AM}{AB}=\frac{AN}{AC} \), et si les points \( \displaystyle A \),\( \displaystyle B \),\( \displaystyle M \) et les points \( \displaystyle A \),\( \displaystyle C \),\( \displaystyle N \) sont alignés dans le même ordre, alors les droites \( \displaystyle (BC) \) et \( \displaystyle (MN) \) sont parallèles.
La condition d'être alignés dans le même ordre est fondamentale. On doit être obligatoirement dans une des 3 configurations ci-dessus!
Le théorème de Thalès permet de calculer des longueurs, tandis que la réciproque du théorème de Thalès permet de montrer que des droites sont parallèles.
Pour montrer que des droites ne sont pas parallèles, on utlise la propriété suivante :
Propriété : (Conséquence admise du théorème de Thalès) Si deux droites \( \displaystyle \left(BM\right)\) et \( \displaystyle \left(CN\right)\) sont sécantes en \( \displaystyle A\) et si deux des rapports \( \displaystyle \frac{AM}{AB}\), \( \displaystyle \frac{AN}{AC}\), \( \displaystyle \frac{MN}{BC}\) ne sont pas égaux, alors le sdroites \( \displaystyle \left(MN\right)\) et \( \displaystyle \left(BC\right)\) ne sont pas parallèles.